1.支持向量機(jī)(SVM)的C參數(shù)
SVM的C參數(shù)為每個錯誤分類的數(shù)據(jù)點增加了代價。如果c小,則對錯誤分類的點的懲罰較低,因此以較大數(shù)量的錯誤分類為代價選擇了具有較大余量的決策邊界。
如果c大,由于高罰分,SVM會嘗試最大程度地減少誤分類示例的數(shù)量,從而導(dǎo)致決策邊界的邊距較小。對于所有錯誤分類的示例,懲罰都不相同。它與到?jīng)Q策邊界的距離成正比。
2.具有RBF內(nèi)核的SVM的Gamma參數(shù)
具有RBF內(nèi)核的SVM的Gamma參數(shù)控制單個訓(xùn)練點的影響距離。 較低的gamma值表示相似半徑較大,這導(dǎo)致將更多點組合在一起。
對于較高的伽瑪值,這些點必須彼此非常接近,以便在同一組(或類)中考慮。因此,具有非常大的伽瑪值的模型往往會過擬合。
3.是什么使邏輯回歸成為線性模型
邏輯回歸的基礎(chǔ)是邏輯函數(shù),也稱為Sigmoid函數(shù),該函數(shù)接受任何實數(shù)值,并將其映射到0到1之間的一個值。
它是一個非線性函數(shù),但邏輯回歸是一個線性模型。
這是我們從S型函數(shù)得到線性方程的方法:
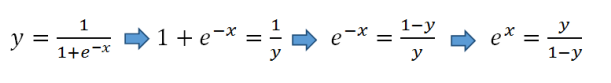
以雙方的自然對數(shù):
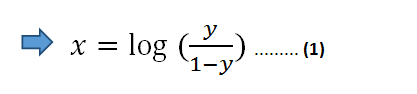
在方程式(1)中,我們可以使用線性方程式z代替x:
然后,等式(1)變?yōu)椋?/p>
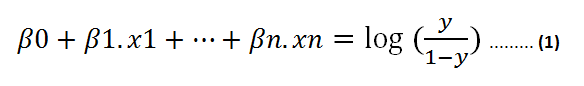
假設(shè)y為正分類的概率。 如果為0.5,則上式的右側(cè)變?yōu)?。
我們現(xiàn)在有一個線性方程要求解。
4. PCA中的主要組成部分
PCA(主成分分析)是一種線性降維算法。 PCA的目標(biāo)是在減少數(shù)據(jù)集的維數(shù)(要素數(shù)量)的同時保留盡可能多的信息。
信息量由方差衡量。具有高方差的特征會告訴我們有關(guān)數(shù)據(jù)的更多信息。
主要成分是原始數(shù)據(jù)集特征的線性組合。
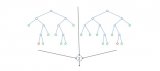
5.隨機(jī)森林
隨機(jī)森林是使用稱為裝袋的方法構(gòu)建的,其中將每個決策樹用作并行估計器。
隨機(jī)森林的成功很大程度上取決于使用不相關(guān)的決策樹。 如果我們使用相同或非常相似的樹,則總體結(jié)果將與單個決策樹的結(jié)果相差無幾。 隨機(jī)森林通過自舉和特征隨機(jī)性來實現(xiàn)具有不相關(guān)的決策樹。
6.梯度增強決策樹(GBDT)
GBDT使用提升方法來組合各個決策樹。 增強意味著將一系列學(xué)習(xí)算法串聯(lián)起來,以從許多順序連接的弱學(xué)習(xí)者中獲得強大的學(xué)習(xí)者。
每棵樹都適合前一棵樹的殘差。 與裝袋不同,加強不涉及自舉采樣。 每次添加新樹時,它都適合初始數(shù)據(jù)集的修改版本。
7.增加隨機(jī)森林和GBDT中的樹的數(shù)量
增加隨機(jī)森林中的樹的數(shù)量不會導(dǎo)致過度擬合。 在某一點之后,模型的準(zhǔn)確性不會因添加更多樹而增加,但也不會因添加過多樹而受到負(fù)面影響。 由于計算原因,您仍然不想添加不必要的樹,但是不存在與隨機(jī)森林中的樹數(shù)相關(guān)聯(lián)的過擬合風(fēng)險。
但是,就過度擬合而言,梯度增強決策樹中的樹數(shù)非常關(guān)鍵。添加過多的樹會導(dǎo)致過擬合,因此一定要停止添加樹,這一點很重要。
8.層次聚類vs K-均值聚類
分層群集不需要預(yù)先指定群集數(shù)量。必須為k均值算法指定簇數(shù)。
它總是生成相同的聚類,而k均值聚類可能會導(dǎo)致不同的聚類,具體取決于質(zhì)心(聚類中心)的啟動方式。
與k均值相比,分層聚類是一種較慢的算法。特別是對于大型數(shù)據(jù)集,運行需要很長時間。
9. DBSCAN算法的兩個關(guān)鍵參數(shù)
DBSCAN是一種聚類算法,可與任意形狀的聚類一起很好地工作。這也是檢測異常值的有效算法。
DBSCAN的兩個關(guān)鍵參數(shù):
eps:指定鄰域的距離。 如果兩個點之間的距離小于或等于eps,則將其視為相鄰點。
minPts:定義集群的最小數(shù)據(jù)點數(shù)。
10. DBSCAN算法中的三種不同類型的點
根據(jù)eps和minPts參數(shù),將點分為核心點,邊界點或離群值:
· 核心點:如果在其半徑為eps的周圍區(qū)域中至少有minPts個點(包括該點本身),則該點為核心點。
· 邊界點:如果一個點可以從核心點到達(dá)并且其周圍區(qū)域內(nèi)的點數(shù)少于minPts,則它是邊界點。
· 離群點:如果一個點不是核心點并且無法從任何核心點到達(dá),則該點就是離群點。
在這種情況下,minPts為4。紅色點是核心點,因為在其周圍區(qū)域內(nèi)至少有4個半徑為eps的點。 該區(qū)域在圖中用圓圈顯示。 黃色點是邊界點,因為它們可以從核心點到達(dá)并且在其鄰域內(nèi)不到4個點。 可到達(dá)意味著在核心點的周圍。 點B和C在其鄰域內(nèi)(即半徑為eps的周圍區(qū)域)有兩個點(包括點本身)。 最后,N是一個離群值,因為它不是核心點,無法從核心點獲得。
11.為什么樸素貝葉斯被稱為樸素?
樸素貝葉斯算法假設(shè)要素彼此獨立,要素之間沒有關(guān)聯(lián)。 但是,現(xiàn)實生活中并非如此。 特征不相關(guān)的這種樸素假設(shè)是將該算法稱為“天真”的原因。
與復(fù)雜算法相比,所有特征都是獨立的這一假設(shè)使樸素貝葉斯算法非常快。在某些情況下,速度比精度更高。
它適用于高維數(shù)據(jù),例如文本分類,電子郵件垃圾郵件檢測。
12.什么是對數(shù)損失?
對數(shù)損失(即交叉熵?fù)p失)是機(jī)器學(xué)習(xí)和深度學(xué)習(xí)模型廣泛使用的成本函數(shù)。
交叉熵量化了兩種概率分布得比較。 在監(jiān)督學(xué)習(xí)任務(wù)中,我們有一個我們要預(yù)測的目標(biāo)變量。 使用交叉熵比較目標(biāo)變量的實際分布和我們的預(yù)測。 結(jié)果是交叉熵?fù)p失,也稱為對數(shù)損失。
13.如何計算對數(shù)損失?
對于每個預(yù)測,都會計算真實類別的預(yù)測概率的負(fù)自然對數(shù)。所有這些值的總和使我們損失了對數(shù)。
這是一個可以更好地解釋計算的示例。
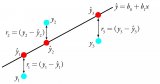
我們有4個類別的分類問題。 我們針對特定觀測值的模型的預(yù)測如下:
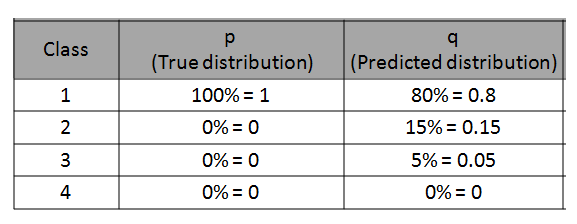
來自此特定觀察值(即數(shù)據(jù)點或行)的對數(shù)損失為-log(0.8)= 0.223。
14.為什么我們使用對數(shù)損失而不是分類準(zhǔn)確性?
在計算對數(shù)損失時,我們采用預(yù)測概率的自然對數(shù)的負(fù)數(shù)。我們對預(yù)測的確定性越高,對數(shù)損失就越低(假設(shè)預(yù)測正確)。
例如,-log(0.9)等于0.10536,-log(0.8)等于0.22314。因此,確定為90%比確定為80%所導(dǎo)致的日志損失更低。
分類,準(zhǔn)確性和召回率等傳統(tǒng)指標(biāo)通過比較預(yù)測的類別和實際類別來評估性能。
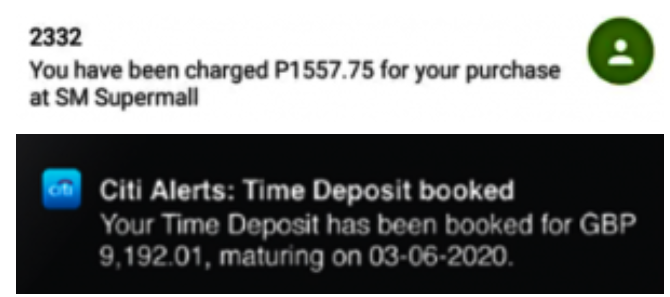
下表顯示了在由5個觀測值組成的相對較小的集合上兩個不同模型的預(yù)測。
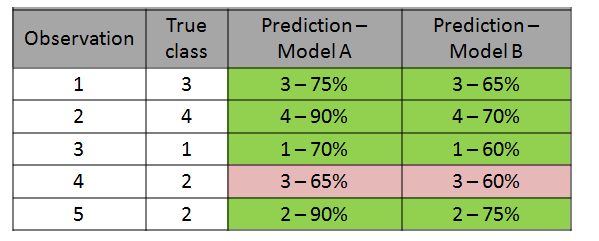
兩種模型都正確地將5個觀測值歸為5個。因此,就分類精度而言,這些模型具有相同的性能。但是,概率表明模型1在預(yù)測中更為確定。因此,總體上可能會表現(xiàn)更好。
對數(shù)損失(即交叉熵?fù)p失)提供了對分類模型的更強大和準(zhǔn)確的評估。
15. ROC曲線和AUC
ROC曲線通過組合所有閾值處的混淆矩陣來總結(jié)性能。 AUC將ROC曲線轉(zhuǎn)化為二進(jìn)制分類器性能的數(shù)字表示。 AUC是ROC曲線下的面積,取值介于0到1之間。AUC表示模型在分離陽性和陰性類別方面的成功程度。
16.精度度和召回率
精度度和召回率指標(biāo)使分類精度進(jìn)一步提高,使我們對模型評估有了更具體的了解。 首選哪一個取決于任務(wù)和我們要實現(xiàn)的目標(biāo)。
精度衡量的是當(dāng)預(yù)測為正時我們的模型有多好。精度的重點是積極的預(yù)測。它表明有多少積極預(yù)測是正確的。
回憶度量了我們的模型在正確預(yù)測肯定類別方面的表現(xiàn)。 召回的重點是實際的正面課堂。 它指示模型能夠正確預(yù)測多少個肯定類別。
結(jié)論
我們已經(jīng)涵蓋了一些基本信息以及有關(guān)機(jī)器學(xué)習(xí)算法的一些細(xì)節(jié)。
有些要點與多種算法有關(guān),例如關(guān)于對數(shù)損失的算法。 這些也很重要,因為評估模型與實施模型同等重要。
所有機(jī)器學(xué)習(xí)算法在某些任務(wù)中都是有用且高效的。根據(jù)您正在執(zhí)行的任務(wù),您可以精通其中的一些。
責(zé)任編輯人:CC
 電子發(fā)燒友App
電子發(fā)燒友App






























評論