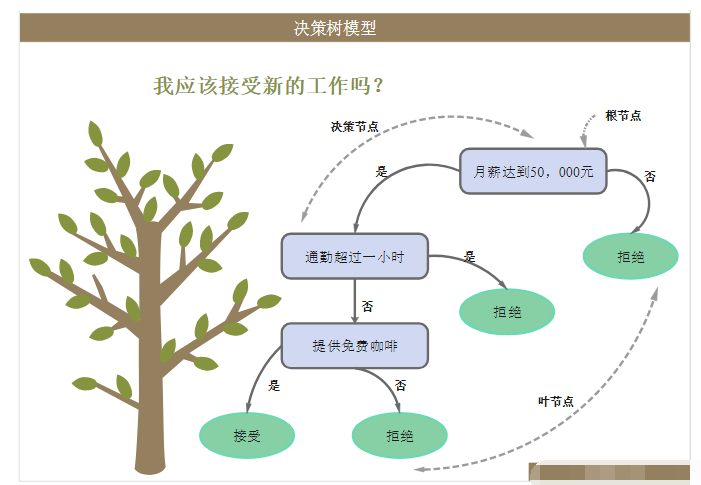
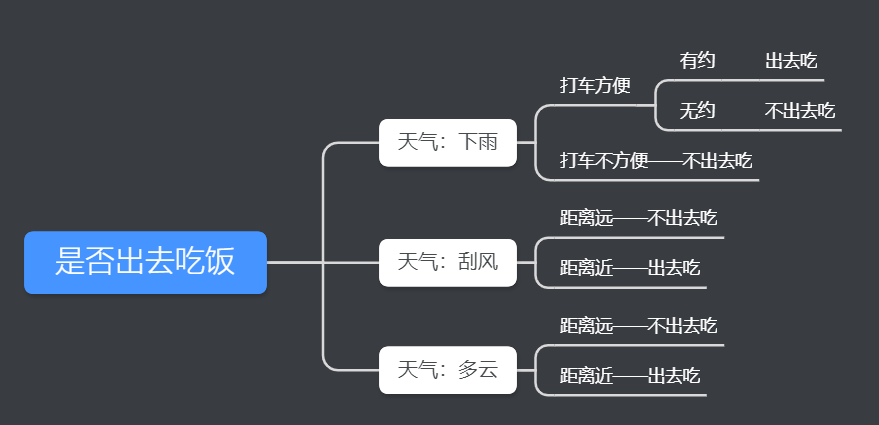
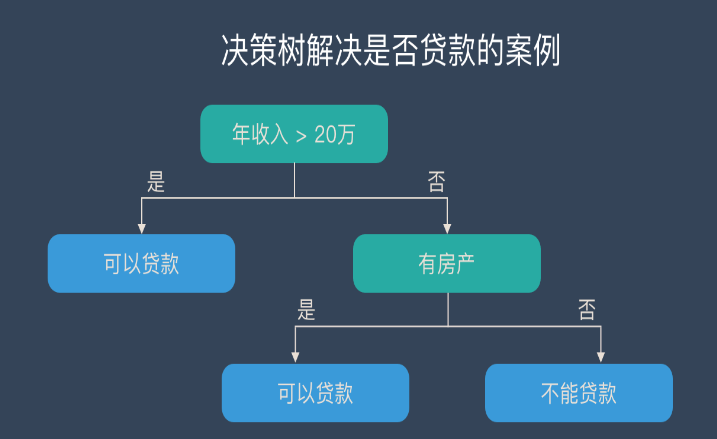
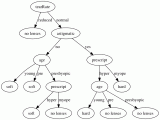
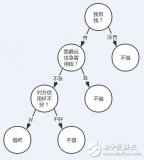
今天,我們介紹機(jī)器學(xué)習(xí)里比較常用的一種分類算法,決策樹。決策樹是對(duì)人類認(rèn)知識(shí)別的一種模擬,給你一堆看似雜亂無章的數(shù)據(jù),如何用盡可能少的特征,對(duì)這些數(shù)據(jù)進(jìn)行有效的分類。
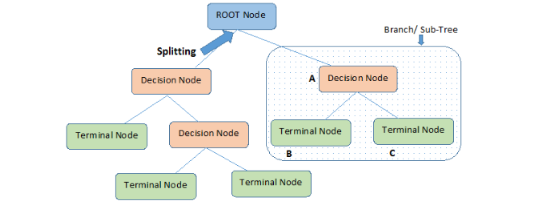
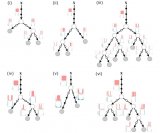
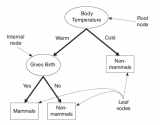
決策樹借助了一種層級(jí)分類的概念,每一次都選擇一個(gè)區(qū)分性最好的特征進(jìn)行分類,對(duì)于可以直接給出標(biāo)簽 label 的數(shù)據(jù),可能最初選擇的幾個(gè)特征就能很好地進(jìn)行區(qū)分,有些數(shù)據(jù)可能需要更多的特征,所以決策樹的深度也就表示了你需要選擇的幾種特征。
在進(jìn)行特征選擇的時(shí)候,常常需要借助信息論的概念,利用最大熵原則。
決策樹一般是用來對(duì)離散數(shù)據(jù)進(jìn)行分類的,對(duì)于連續(xù)數(shù)據(jù),可以事先對(duì)其離散化。
在介紹決策樹之前,我們先簡(jiǎn)單的介紹一下信息熵,我們知道,熵的定義為:

?
我們先構(gòu)造一些簡(jiǎn)單的數(shù)據(jù):
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
import math
import operator
def Create_data():
dataset = [[1,1,‘yes’],
[1, 1,‘yes’],
[1, 0, ‘no’],
[0, 1, ‘no’],
[0, 1, ‘no’],
[3, 0, ‘maybe’]]
feat_name = [‘no surfacing’, ‘flippers’]
return dataset, feat_name
然后定義一個(gè)計(jì)算熵的函數(shù):
def Cal_entrpy(dataset):
n_sample = len(dataset)
n_label = {}
for featvec in dataset:
current_label = featvec[-1]
if current_label not in n_label.keys():
n_label[current_label] = 0
n_label[current_label] += 1
shannonEnt = 0.0
for key in n_label:
prob = float(n_label[key]) / n_sample
shannonEnt -= prob * math.log(prob, 2)
return shannonEnt
要注意的是,熵越大,說明數(shù)據(jù)的類別越分散,越呈現(xiàn)某種無序的狀態(tài)。
下面再定義一個(gè)拆分?jǐn)?shù)據(jù)集的函數(shù):
def Split_dataset(dataset, axis, value):
retDataSet = []
for featVec in dataset:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1 :])
retDataSet.append(reducedFeatVec)
return retDataSet
結(jié)合前面的幾個(gè)函數(shù),我們可以構(gòu)造一個(gè)特征選擇的函數(shù):
def Choose_feature(dataset):
num_sample = len(dataset)
num_feature = len(dataset[0]) - 1
baseEntrpy = Cal_entrpy(dataset)
best_Infogain = 0.0
bestFeat = -1
for i in range (num_feature):
featlist = [example[i] for example in dataset]
uniquValus = set(featlist)
newEntrpy = 0.0
for value in uniquValus:
subData = Split_dataset(dataset, i, value)
prob = len(subData) / float(num_sample)
newEntrpy += prob * Cal_entrpy(subData)
info_gain = baseEntrpy - newEntrpy
if (info_gain 》 best_Infogain):
best_Infogain = info_gain
bestFeat = i
return bestFeat
然后再構(gòu)造一個(gè)投票及計(jì)票的函數(shù)
def Major_cnt(classlist):
class_num = {}
for vote in classlist:
if vote not in class_num.keys():
class_num[vote] = 0
class_num[vote] += 1
Sort_K = sorted(class_num.iteritems(),
key = operator.itemgetter(1), reverse=True)
return Sort_K[0][0]
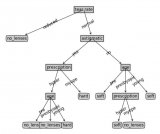
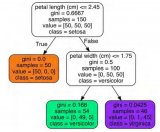
有了這些,就可以構(gòu)造我們需要的決策樹了:
def Create_tree(dataset, featName):
classlist = [example[-1] for example in dataset]
if classlist.count(classlist[0]) == len(classlist):
return classlist[0]
if len(dataset[0]) == 1:
return Major_cnt(classlist)
bestFeat = Choose_feature(dataset)
bestFeatName = featName[bestFeat]
myTree = {bestFeatName: {}}
del(featName[bestFeat])
featValues = [example[bestFeat] for example in dataset]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = featName[:]
myTree[bestFeatName][value] = Create_tree(Split_dataset
(dataset, bestFeat, value), subLabels)
return myTree
def Get_numleafs(myTree):
numLeafs = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == ‘dict’ :
numLeafs += Get_numleafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def Get_treedepth(myTree):
max_depth = 0
firstStr = myTree.keys()[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == ‘dict’ :
this_depth = 1 + Get_treedepth(secondDict[key])
else:
this_depth = 1
if this_depth 》 max_depth:
max_depth = this_depth
return max_depth
 電子發(fā)燒友App
電子發(fā)燒友App















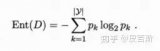











評(píng)論