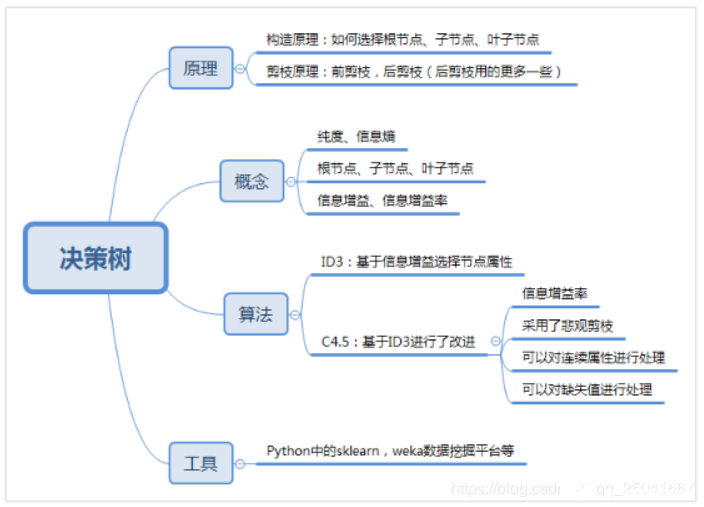
概述
決策樹(Decision Tree)是在已知各種情況發(fā)生概率的基礎(chǔ)上,通過構(gòu)成決策樹來求取凈現(xiàn)值的期望值大于等于零的概率,評價項目風險,判斷其可行性的決策分析方法,是直觀運用概率分析的一種圖解法。由于這種決策分支畫成圖形很像一棵樹的枝干,故稱決策樹。在機器學習中,決策樹是一個預測模型,他代表的是對象屬性與對象值之間的一種映射關(guān)系。Entropy = 系統(tǒng)的凌亂程度,使用算法ID3, C4.5和C5.0生成樹算法使用熵。這一度量是基于信息學理論中熵的概念。
決策樹是一種樹形結(jié)構(gòu),其中每個內(nèi)部節(jié)點表示一個屬性上的測試,每個分支代表一個測試輸出,每個葉節(jié)點代表一種類別。
分類樹(決策樹)是一種十分常用的分類方法。他是一種監(jiān)管學習,所謂監(jiān)管學習就是給定一堆樣本,每個樣本都有一組屬性和一個類別,這些類別是事先確定的,那么通過學習得到一個分類器,這個分類器能夠?qū)π鲁霈F(xiàn)的對象給出正確的分類。這樣的機器學習就被稱之為監(jiān)督學習。
畫法
機器學習中,決策樹是一個預測模型;他代表的是對象屬性與對象值之間的一種映射關(guān)系。樹中每個節(jié)點表示某個對象,而每個分叉路徑則代表的某個可能的屬性值,而每個葉結(jié)點則對應從根節(jié)點到該葉節(jié)點所經(jīng)歷的路徑所表示的對象的值。決策樹僅有單一輸出,若欲有復數(shù)輸出,可以建立獨立的決策樹以處理不同輸出。
數(shù)據(jù)挖掘中決策樹是一種經(jīng)常要用到的技術(shù),可以用于分析數(shù)據(jù),同樣也可以用來作預測。
從數(shù)據(jù)產(chǎn)生決策樹的機器學習技術(shù)叫做決策樹學習, 通俗說就是決策樹。
一個決策樹包含三種類型的節(jié)點:
① 決策節(jié)點:通常用矩形框來表示。
是對幾種可能方案的選擇,即最后選擇的最佳方案。
如果決策屬于多級決策,則決策樹的中間可以有多個決策點,
以決策樹根部的決策點為最終決策方案。
② 機會節(jié)點:通常用圓圈來表示。
代表備選方案的經(jīng)濟效果(期望值),
通過各狀態(tài)節(jié)點的經(jīng)濟效果的對比,
按照一定的決策標準就可以選出最佳方案。
由狀態(tài)節(jié)點引出的分支稱為概率枝,
概率枝的數(shù)目表示可能出現(xiàn)的自然狀態(tài)數(shù)目每個分枝上要注明該狀態(tài)出現(xiàn)的概率。
③ 終結(jié)點:通常用三角形來表示。
將每個方案在各種自然狀態(tài)下取得的損益值標注于結(jié)果節(jié)點的右端。
決策樹學習也是資料探勘中一個普通的方法。在這里,每個決策樹都表述了一種樹型結(jié)構(gòu),它由它的分支來對該類型的對象依靠屬性進行分類。每個決策樹可以依靠對源數(shù)據(jù)庫的分割進行數(shù)據(jù)測試。這個過程可以遞歸式的對樹進行修剪。 當不能再進行分割或一個單獨的類可以被應用于某一分支時,遞歸過程就完成了。另外,隨機森林分類器將許多決策樹結(jié)合起來以提升分類的正確率。
決策樹同時也可以依靠計算條件概率來構(gòu)造。
剪枝
剪枝是決策樹停止分支的方法之一,剪枝有分預先剪枝和后剪枝兩種。
預先剪枝是在樹的生長過程中設(shè)定一個指標,當達到該指標時就停止生長,這樣做容易產(chǎn)生“視界局限”,就是一旦停止分支,使得節(jié)點N成為葉節(jié)點,就斷絕了其后繼節(jié)點進行“好”的分支操作的任何可能性。不嚴格的說這些已停止的分支會誤導學習算法,導致產(chǎn)生的樹不純度降差最大的地方過分靠近根節(jié)點。
后剪枝中樹首先要充分生長,直到葉節(jié)點都有最小的不純度值為止,因而可以克服“視界局限”。然后對所有相鄰的成對葉節(jié)點考慮是否消去它們,如果消去能引起令人滿意的不純度增長,那么執(zhí)行消去,并令它們的公共父節(jié)點成為新的葉節(jié)點。這種“合并”葉節(jié)點的做法和節(jié)點分支的過程恰好相反,經(jīng)過剪枝后葉節(jié)點常常會分布在很寬的層次上,樹也變得非平衡。
后剪枝技術(shù)的優(yōu)點是克服了“視界局限”效應,而且無需保留部分樣本用于交叉驗證,所以可以充分利用全部訓練集的信息。但后剪枝的計算量代價比預剪枝方法大得多,特別是在大樣本集中,不過對于小樣本的情況,后剪枝方法還是優(yōu)于預剪枝方法的。
決策樹的優(yōu)缺點
優(yōu)點
決策樹易于理解和實現(xiàn),人們在在學習過程中不需要使用者了解很多的背景知識,這同時是它的能夠直接體現(xiàn)數(shù)據(jù)的特點,只要通過解釋后都有能力去理解決策樹所表達的意義。
對于決策樹,數(shù)據(jù)的準備往往是簡單或者是不必要的,而且能夠同時處理數(shù)據(jù)型和常規(guī)型屬性,在相對短的時間內(nèi)能夠?qū)Υ笮蛿?shù)據(jù)源做出可行且效果良好的結(jié)果。
易于通過靜態(tài)測試來對模型進行評測,可以測定模型可信度;如果給定一個觀察的模型,那么根據(jù)所產(chǎn)生的決策樹很容易推出相應的邏輯表達式。
缺點
對連續(xù)性的字段比較難預測。
對有時間順序的數(shù)據(jù),需要很多預處理的工作。
當類別太多時,錯誤可能就會增加的比較快。
一般的算法分類的時候,只是根據(jù)一個字段來分類。
ID3算法
決策樹基本上就是把我們以前的經(jīng)驗總結(jié)出來。
如果我們要出門打籃球,一般會根據(jù)“天氣”、“溫度”、“濕度”、“刮風”這幾個條件來判斷,最后得到結(jié)果:去打籃球?還是不去?
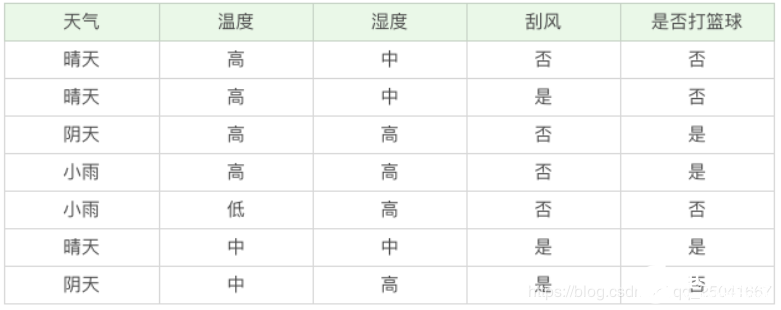
在這里我們先介紹兩個指標:純度和信息熵。
純度
你可以把決策樹的構(gòu)造過程理解成為尋找純凈劃分的過程。數(shù)學上,我們可以用純度來表示,純度換一種方式來解釋就是讓目標變量的分歧最小。
舉個例子,假設(shè)有 3 個集合:
集合 1:6 次都去打籃球;
集合 2:4 次去打籃球,2 次不去打籃球;
集合 3:3 次去打籃球,3 次不去打籃球。
按照純度指標來說,集合 1》 集合 2》 集合 3。因為集合1 的分歧最小,集合 3 的分歧最大。
信息熵
表示信息的不確定度
在信息論中,隨機離散事件出現(xiàn)的概率存在著不確定性。為了衡量這種信息的不確定性,信息學之父香農(nóng)引入了信息熵的概念,并給出了計算信息熵的數(shù)學公式:
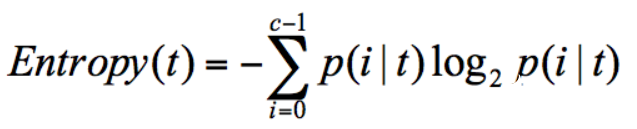
p(i|t) 代表了節(jié)點 t 為分類 i 的概率,其中 log2 為取以 2 為底的對數(shù)。存在一種度量,它能幫我們反映出來這個信息的不確定度。當不確定性越大時,它所包含的信息量也就越大,信息熵也就越高。
舉個例子,假設(shè)有 2 個集合:
? 集合 1:5 次去打籃球,1 次不去打籃球;
? 集合 2:3 次去打籃球,3 次不去打籃球。
在集合 1 中,有 6 次決策,其中打籃球是 5 次,不打籃球是 1 次。那么假設(shè):類別 1 為“打籃球”,即次數(shù)為 5;類別 2 為“不打籃球”,即次數(shù)為 1。那么節(jié)點劃分為類別1的概率是 5/6,為類別2的概率是1/6,帶入上述信息熵公式可以計算得出:
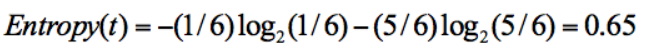
同樣,集合 2 中,也是一共 6 次決策,其中類別 1 中“打籃球”的次數(shù)是 3,類別 2“不打籃球”的次數(shù)也是 3,那么信息熵為多少呢?我們可以計算得出:
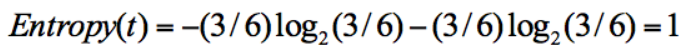
從上面的計算結(jié)果中可以看出,信息熵越大,純度越低。當集合中的所有樣本均勻混合時,信息熵最大,純度最低。
我們在構(gòu)造決策樹的時候,會基于純度來構(gòu)建。而經(jīng)典的 “不純度”的指標有三種,分別是信息增益(ID3 算法)、信息增益率(C4.5 算法)以及基尼指數(shù)(Cart 算法)。
信息增益
信息增益指的就是劃分可以帶來純度的提高,信息熵的下降。它的計算公式,是父親節(jié)點的信息熵減去所有子節(jié)點的信息熵。在計算的過程中,我們會計算每個子節(jié)點的歸一化信息熵,即按照每個子節(jié)點在父節(jié)點中出現(xiàn)的概率,來計算這些子節(jié)點的信息熵。
所以信息增益的公式可以表示為:
公式中 D 是父親節(jié)點,Di 是子節(jié)點,Gain(D,a)中的 a 作為 D 節(jié)點的屬性選擇。
假設(shè)D 天氣 = 晴的時候,會有 5 次去打籃球,5 次不打籃球。其中 D1 刮風 = 是,有 2 次打籃球,1 次不打籃球。D2 刮風 = 否,有 3 次打籃球,4 次不打籃球。那么a 代表節(jié)點的屬性,即天氣 = 晴。
針對圖上這個例子,D 作為節(jié)點的信息增益為:
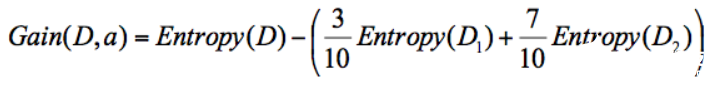
也就是 D 節(jié)點的信息熵 -2 個子節(jié)點的歸一化信息熵。2個子節(jié)點歸一化信息熵 =3/10 的 D1 信息熵 +7/10 的 D2 信息熵。
我們基于 ID3 的算法規(guī)則,完整地計算下我們的訓練集,訓練集中一共有 7 條數(shù)據(jù),3 個打籃球,4 個不打籃球,所以根節(jié)點的信息熵是:
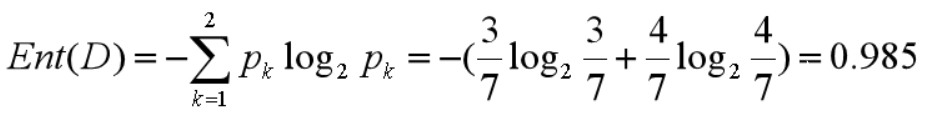
如果你將天氣作為屬性的劃分,會有三個葉子節(jié)點 D1、D2 和D3,分別對應的是晴天、陰天和小雨。我們用 + 代表去打籃球,- 代表不去打籃球。那么第一條記錄,晴天不去打籃球,可以記為 1-,于是我們可以用下面的方式來記錄 D1,D2,D3:
D1(天氣 = 晴天)={1-,2-,6+}
D2(天氣 = 陰天)={3+,7-}
D3(天氣 = 小雨)={4+,5-}
我們先分別計算三個葉子節(jié)點的信息熵:
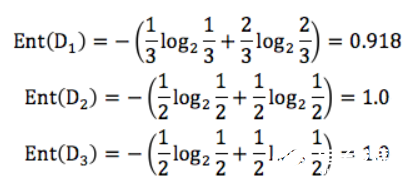
因為 D1 有 3 個記錄,D2 有 2 個記錄,D3 有2 個記錄,所以 D 中的記錄一共是 3+2+2=7,即總數(shù)為 7。所以 D1 在 D(父節(jié)點)中的概率是 3/7,D2在父節(jié)點的概率是 2/7,D3 在父節(jié)點的概率是 2/7。那么作為子節(jié)點的歸一化信息熵 = 3/70.918+2/71.0=0.965。
因為我們用 ID3 中的信息增益來構(gòu)造決策樹,所以要計算每個節(jié)點的信息增益。
天氣作為屬性節(jié)點的信息增益為,Gain(D , 天氣)=0.985-0.965=0.020。
同理我們可以計算出其他屬性作為根節(jié)點的信息增益,它們分別為:
Gain(D , 溫度)=0.128
Gain(D , 濕度)=0.020
Gain(D , 刮風)=0.020
我們能看出來溫度作為屬性的信息增益最大。因為 ID3 就是要將信息增益最大的節(jié)點作為父節(jié)點,這樣可以得到純度高的決策樹,所以我們將溫度作為根節(jié)點。其決策樹狀圖分裂為下圖所示:
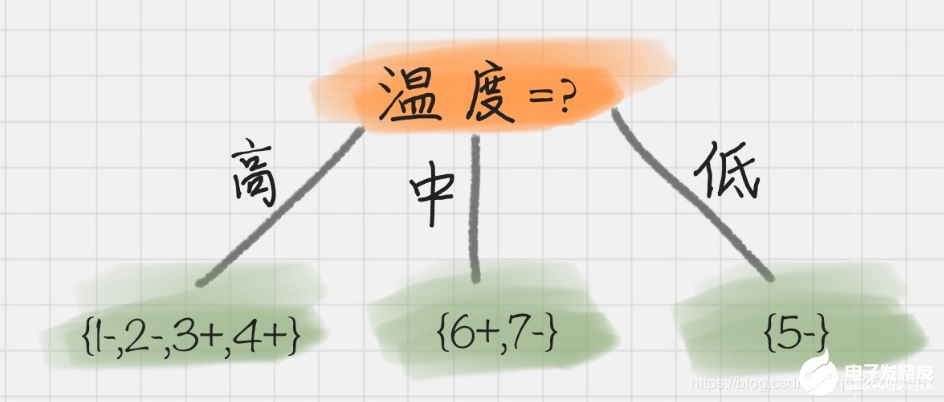
然后我們要將上圖中第一個葉節(jié)點,也就是 D1={1-,2-,3+,4+}進一步進行分裂,往下劃分,計算其不同屬性(天氣、濕度、刮風)作為節(jié)點的信息增益,可以得到:
Gain(D , 天氣)=0
Gain(D , 濕度)=0
Gain(D , 刮風)=0.0615
我們能看到刮風為 D1 的節(jié)點都可以得到最大的信息增益,這里我們選取刮風作為節(jié)點。同理,我們可以按照上面的計算步驟得到完整的決策樹,結(jié)果如下:
于是我們通過 ID3 算法得到了一棵決策樹。ID3 的算法規(guī)則相對簡單,可解釋性強。同樣也存在缺陷,比如我們會發(fā)現(xiàn)ID3 算法傾向于選擇取值比較多的屬性。這樣,如果我們把“編號”作為一個屬性(一般情況下不會這么做,這里只是舉個例子),那么“編號”將會被選為最優(yōu)屬性 。但實際上“編號”是無關(guān)屬性的,它對“打籃球”的分類并沒有太大作用。
所以 ID3 有一個缺陷就是,有些屬性可能對分類任務沒有太大作用,但是他們?nèi)匀豢赡軙贿x為最優(yōu)屬性。這種缺陷不是每次都會發(fā)生,只是存在一定的概率。在大部分情況下,ID3 都能生成不錯的決策樹分類。針對可能發(fā)生的缺陷,后人提出了新的算法進行改進。
C4.5 算法
信息增益率
因為 ID3 在計算的時候,傾向于選擇取值多的屬性。為了避免這個問題,C4.5 采用信息增益率的方式來選擇屬性。信息增益率 = 信息增益 / 屬性熵
當屬性有很多值的時候,相當于被劃分成了許多份,雖然信息增益變大了,但是對于 C4.5 來說,屬性熵也會變大,所以整體的信息增益率并不大。
悲觀剪枝
ID3 構(gòu)造決策樹的時候,容易產(chǎn)生過擬合的情況。在 C4.5中,會在決策樹構(gòu)造之后采用悲觀剪枝(PEP),這樣可以提升決策樹的泛化能力。
悲觀剪枝是后剪枝技術(shù)中的一種,通過遞歸估算每個內(nèi)部節(jié)點的分類錯誤率,比較剪枝前后這個節(jié)點的分類錯誤率來決定是否對其進行剪枝。這種剪枝方法不再需要一個單獨的測試數(shù)據(jù)集。
離散化處理連續(xù)屬性
C4.5 可以處理連續(xù)屬性的情況,對連續(xù)的屬性進行離散化的處理。比如打籃球存在的“濕度”屬性,不按照“高、中”劃分,而是按照濕度值進行計算,那么濕度取什么值都有可能。該怎么選擇這個閾值呢,C4.5 選擇具有最高信息增益的劃分所對應的閾值。
處理缺失值
針對數(shù)據(jù)集不完整的情況,C4.5 也可以進行處理。
假如我們得到的是如下的數(shù)據(jù),你會發(fā)現(xiàn)這個數(shù)據(jù)中存在兩點問題。第一個問題是,數(shù)據(jù)集中存在數(shù)值缺失的情況,如何進行屬性選擇?第二個問題是,假設(shè)已經(jīng)做了屬性劃分,但是樣本在這個屬性上有缺失值,該如何對樣本進行劃分?
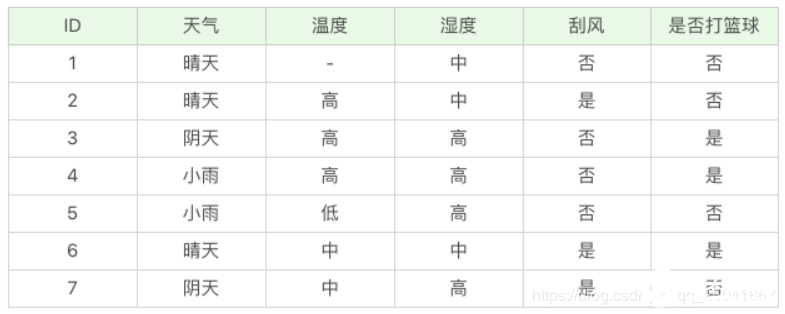
我們不考慮缺失的數(shù)值,可以得到溫度 D={2-,3+,4+,5-,6+,7-}。溫度 = 高:D1={2-,3+,4+};溫度 = 中:D2={6+,7-};溫度 = 低:D3={5-} 。這里 + 號代表打籃球,- 號代表不打籃球。比如ID=2 時,決策是不打籃球,我們可以記錄為 2-。
所以三個葉節(jié)點的信息熵可以結(jié)算為:
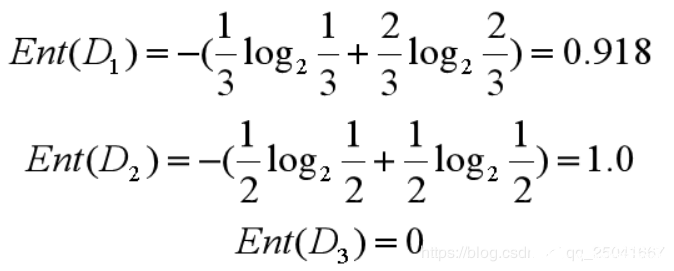
這三個節(jié)點的歸一化信息熵為 3/60.918+2/61.0+1/6*0=0.792。
針對將屬性選擇為溫度的信息增益率為:
Gain(D′, 溫度)=Ent(D′)-0.792=1.0-0.792=0.208
D′的樣本個數(shù)為 6,而 D 的樣本個數(shù)為 7,所以所占權(quán)重比例為 6/7,所以 Gain(D′,溫度) 所占權(quán)重比例為6/7,所以:
Gain(D, 溫度)=6/7*0.208=0.178
這樣即使在溫度屬性的數(shù)值有缺失的情況下,我們依然可以計算信息增益,并對屬性進行選擇。
小結(jié)
首先 ID3 算法的優(yōu)點是方法簡單,缺點是對噪聲敏感。訓練數(shù)據(jù)如果有少量錯誤,可能會產(chǎn)生決策樹分類錯誤。C4.5 在 IID3 的基礎(chǔ)上,用信息增益率代替了信息增益,解決了噪聲敏感的問題,并且可以對構(gòu)造樹進行剪枝、處理連續(xù)數(shù)值以及數(shù)值缺失等情況,但是由于 C4.5 需要對數(shù)據(jù)集進行多次掃描,算法效率相對較低。
-
機器學習
+關(guān)注
關(guān)注
66文章
8438瀏覽量
132928 -
決策樹
+關(guān)注
關(guān)注
3文章
96瀏覽量
13573
發(fā)布評論請先 登錄
相關(guān)推薦




 詳解機器學習決策樹的優(yōu)缺點
詳解機器學習決策樹的優(yōu)缺點










評論