決策樹模型是白盒模型的一種，其預測結(jié)果可以由人來解釋。我們把機器學習模型的這一特性稱為可解釋性，但并不是所有的機器學習模型都具有可解釋性。

作為可解釋性屬性的一部分，特征重要性是一個衡量每個輸入特征對模型預測結(jié)果貢獻的指標，即某個特征上的微小變化如何改變預測結(jié)果。

直覺

不同于基尼不純度或熵，沒有一個通用的數(shù)學公式來定義特征的重要性，而特征的重要性在不同的模型中是不同的。

例如，對于線性回歸模型，假設(shè)所有輸入特征具有相同的尺度（如［0，1］，那么每個特征的特征重要性就是與該特征相關(guān)的權(quán)值的絕對值。從這個公式可以看出線性回歸模型的f （X） =∑i = 1 n （wixi），模型的結(jié)果是線性正比于每個組件（wixi）這是由重量決定的（wi）的組件。

對于決策樹，為了度量特征的重要性，我們需要研究模型，看看每個特征是如何在模型的最終“決策”中發(fā)揮作用的。從前面的文章中我們了解到，在決策樹模型中，在每個決策節(jié)點上，我們選擇最佳的特征進行分割，以便進一步區(qū)分到達該決策節(jié)點的樣本。在每一次分割中，我們都更接近最終的決定（即葉節(jié)點）。因此，我們可以說，在每個決策節(jié)點上，所選擇的分割特征決定了最終的預測結(jié)果。直觀地說，我們也可以說，那些被選擇的特征比那些實際上在決策過程中沒有作用的非被選擇的特征更重要。現(xiàn)在，剩下的問題是我們?nèi)绾瘟炕睾饬窟@種重要性。

有人可能還記得，我們使用信息增益或基尼系數(shù)來衡量分割的質(zhì)量。當然，還可以將增益與所選擇的特性關(guān)聯(lián)起來，并使用增益來量化該特性在這個特定的分裂發(fā)生時的貢獻。此外，我們可以累積決策樹中出現(xiàn)的每個特征的增益。

最后，每個特征的累積增益可以作為決策樹模型的特征重要性。

另一方面，作為一個可能會注意到，這一決定節(jié)點不是同樣重要的是，自從決定節(jié)點樹的根可以幫助過濾所有的輸入樣本，而決定節(jié)點樹的底部有助于區(qū)分總樣本的只有少數(shù)。因此，一個特征在每個決策節(jié)點獲得的增益的權(quán)重并不相同，即一個特征在一個決策節(jié)點獲得的增益應(yīng)按該決策節(jié)點幫助區(qū)分的樣本比例進行加權(quán)。

基于上述直覺，我們可以推導出以下公式來計算決策樹中每個特征的重要性I：

注：我們可以用上述公式中的信息增益來代替基尼系數(shù)增益度量，只要我們對所有特征都使用相同的度量。

通過上面的公式，我們可以得到一個值來衡量決策樹中每個特征的重要性。有時，可能需要對值進行規(guī)范化，以便更直觀地比較這些值，即將所有值縮放到（0，1）的范圍內(nèi)。例如，如果有兩個特征經(jīng)過歸一化后得分相同（即0.5），我們可以說它們在決策樹中同等重要。

舉個例子

讓我們看一個具體的例子，看看我們?nèi)绾螒?yīng)用上面的公式來計算決策樹中的特征重要性。首先，我們在下圖中展示了一個實例決策樹。

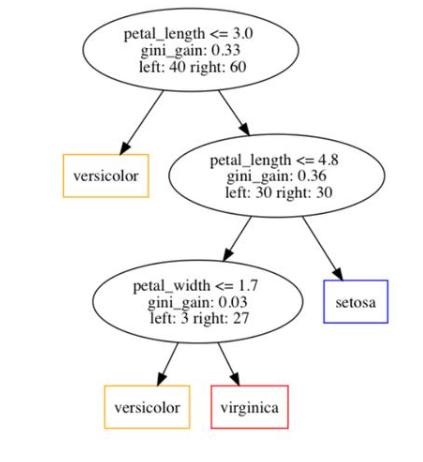
從圖中可以看出，該樹中共有3個決策節(jié)點。在每個決策節(jié)點中，我們指出了三條信息：

1、選擇要分割的特性。

2、特征獲得的基尼系數(shù)

3、分別分配給左子節(jié)點和右子節(jié)點的樣本數(shù)量。

此外，我們可以看出決策樹總共訓練了100個樣本。

因此，我們可以計算出樹中涉及的兩個特征的特征重要性如下：

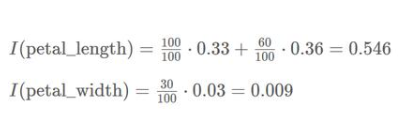
進一步，我們可以得到歸一化特征重要性如下：

后記：路漫漫其修遠兮，吾將上下而求索！