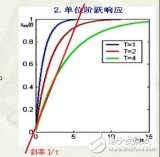
表示過渡反應(yīng)的時間過程的常數(shù)。指該物理量從最大值衰減到最大值的1/e所需要的時間。對于某一按指數(shù)規(guī)律衰變的量,其幅值衰變?yōu)?/e倍時所需的時間稱為時間常數(shù)。 在不同的應(yīng)用領(lǐng)域中,時間常數(shù)也有不同的具體含義。
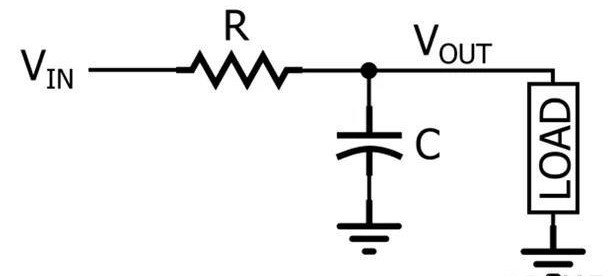
RC電路:t=RC;
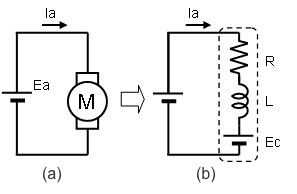
LR電路:t=L/R;
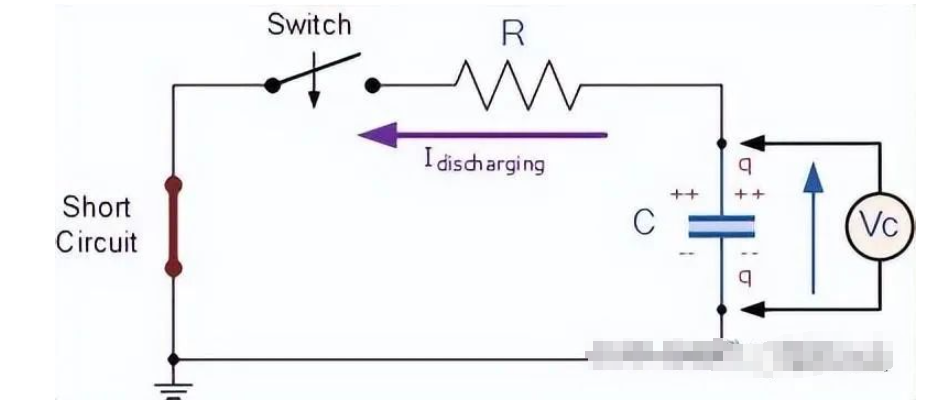
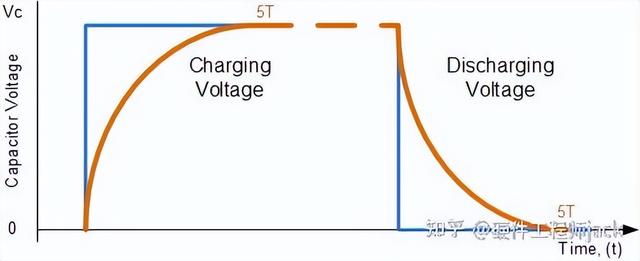
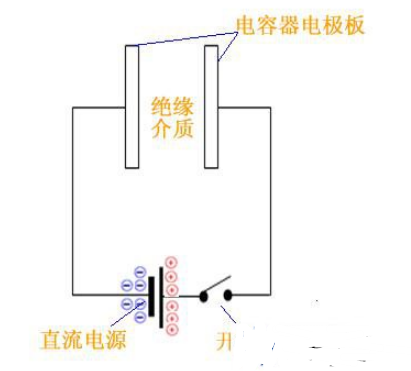
在RC電路中,電容電壓Uc總是由初始值Uc(0)按指數(shù)規(guī)律單調(diào)的衰減到零,其時間常數(shù)=R*C
在RL電路中,iL總是由初始值iL(0)按指數(shù)規(guī)律單調(diào)的衰減到零,其時間常數(shù)=L/R
現(xiàn)在,我們介紹幾種確定時間常數(shù)的常見方法。
[方法 1]如果列出的電路方程為τdx( t) / dt + x( t) = aw( t) ( 1) 式中,x( t) 和 w( t) 分別為電路電壓或電流變量和電路激勵; τ 和 a 為常數(shù),τ 就是電路的時間常數(shù),即時間常數(shù)等于一階電路方程特征根倒數(shù)的負(fù)值。這個方法的優(yōu)點是比較直觀,缺點是必須列寫電路方程,求解過程顯得較為復(fù)雜。
[方法 2]當(dāng)一階電路僅包含一個動態(tài)元件( 或雖包含若干個同類型的動態(tài)元件但這些動態(tài)元件可等效為一個動態(tài)元件) 時,首先求出從動態(tài)元件( 或等效動態(tài)元件) 兩端看進(jìn)去的等效電阻,然后可利用 τ = RC 或 τ = L /R 計算出時間常數(shù)。這是一種比較簡單的計算時間常數(shù)的方法,大多數(shù)一階電路的時間常數(shù)都可按該方法確定。
[方法 3]從式( 1) 可以看出,一階電路的時間常數(shù)與電路的激勵無關(guān)。為方便起見,在求時間常數(shù)時可將電路的激勵( 電壓源或電流源) 置零,然后利用 τ = RC 或 τ = L /R 就可以計算出時間常數(shù)。
[方法 4]時間常數(shù)等于一階電路固有頻率倒數(shù)的負(fù)值,因此如能求得電路的 s 域網(wǎng)絡(luò)函數(shù),則通過網(wǎng)絡(luò)函數(shù)也可求得時間常數(shù)。
對于簡單的一階電路,時間常數(shù)的確定可采用上述任一方法。當(dāng)一階電路具有較復(fù)雜的形式時,則上述方法的繁簡程度有較大的區(qū)別。
電路中的時間常數(shù)L/R中的R是怎么看的
簡單的方法,考慮一下,戴維寧電路中等效電阻如何計算的,就知道是怎么回事了。
做法是,把動態(tài)元件移除,對剩下的一端口電路求等效電阻即可,由于剩下的一端口電路是含源網(wǎng)絡(luò),所以先將獨立源置0(即電流源開路,電壓源短路),然后對該網(wǎng)絡(luò)求輸入電阻就是要求的等效電阻!對于該問題則有Re
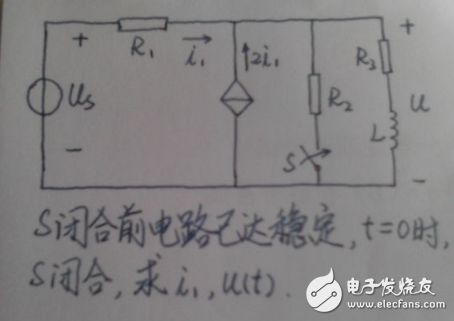
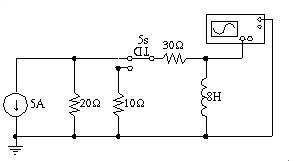
例子1:電路如圖,求時間常數(shù)τ

時間常數(shù):T=ReqC
因Req=1//(2//2+3)=0.8k歐,
故T=0.8x5=4ms。
例子2:一階電路的時間常數(shù)怎么求?求等效電阻的時候那個受控源應(yīng)該怎么處理?
先求出等效電阻。(就是從電感哪里看進(jìn)去的。)求等效電阻要先把電壓源變成導(dǎo)線。因為有受控源,求等效電阻你只能設(shè)從L處加電壓U然后求出電流I然后等效電阻就是U/I了。(或設(shè)電流求電壓)
這題的等效電阻是(1/3)R1+R2×R3/(R2+R3)
然后時間常數(shù)就是L/R
例子3:時間常數(shù)怎么求?τ=RC,怎么確定r和c?圖中電路的RC是怎么確定的?
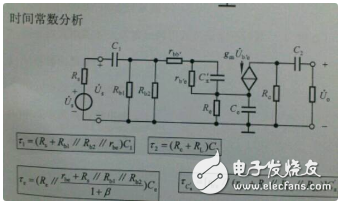
按照圖中的標(biāo)識,如果你要求的是Uc1(t),那么時間常數(shù)中的C就是C1的電容。同理知道其他。而時間常數(shù)中的R,有時候需要用短路法求(將電容短路,求出短路電流,再通過斷路時的端電壓,根據(jù)R=U/I可求。)另外一種方法是外施電源法(將電容拿掉,替換一個電源,可以是電壓源,也可以是電流源,求出電流,一般是帶假設(shè)的電源電壓,可以約掉。)
例子4:電路時間常數(shù)怎么求
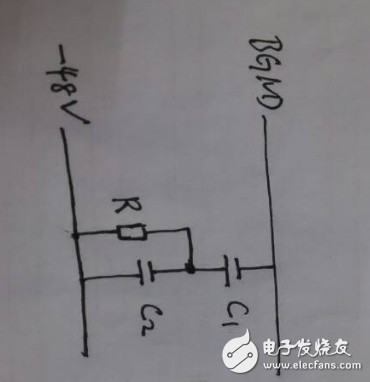
一端接電源,另一端開路?如果是這樣的電源除源后求電阻兩端的電容,由于電壓源除源是短路,C1、C2相當(dāng)于并聯(lián),所以電路的時間常數(shù)τ=R(C1+C2)
 電子發(fā)燒友App
電子發(fā)燒友App










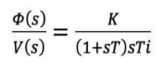
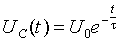
















評論