什么是RC的時間常數:
RC的時間常數:表示過渡反應的時間過程的常數。在電阻、電容的電路中,它是電阻和電容的乘積。若C的單位是μF(微法),R的單位是MΩ(兆歐),時間常數的單位就是秒。在這樣的電路中當恒定電流I流過時,電容的端電壓達到最大值(等于IR)的1-1/e時即約0.63倍所需要的時間即是時間常數 ,而在電路斷開時,時間常數是電容的端電壓達到最大值的1/e,即約0.37倍時所需要的時間。
RLC暫態電路時間常數是在RC電路中,電容電壓Uc總是由初始值UC(0)按指數規律單調的衰減到零,其時間常數 =RC。
時間常數RC的計算方法:
進入正題前,我們先來回顧下電容的充放電時間計算公式,假設有電源Vu通過電阻R給電容C充電,V0為電容上的初始電壓值,Vu為電容充滿電后的電壓值,Vt為任意時刻t時電容上的電壓值,那么便可以得到如下的計算公式:
Vt = V0 + (Vu – V0) * [1 – exp( -t/RC)]
如果電容上的初始電壓為0,則公式可以簡化為:
Vt = Vu * [1 – exp( -t/RC)]
由上述公式可知,因為指數值只可能無限接近于0,但永遠不會等于0,所以電容電量要完全充滿,需要無窮大的時間。
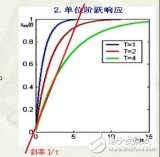
當t = RC時,Vt = 0.63Vu;
當t = 2RC時,Vt = 0.86Vu;
當t = 3RC時,Vt = 0.95Vu;
當t = 4RC時,Vt = 0.98Vu;
當t = 5RC時,Vt = 0.99Vu;
可見,經過3~5個RC后,充電過程基本結束。
當電容充滿電后,將電源Vu短路,電容C會通過R放電,則任意時刻t,電容上的電壓為:
Vt = Vu * exp( -t/RC)
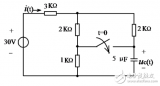
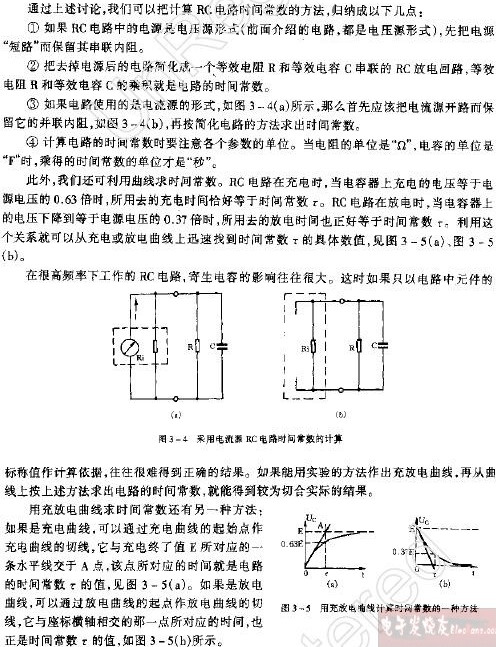
對于簡單的串聯電路,時間常數就等于電阻R和電容C的乘積,但是,在實際電路中,時間常數RC并不那么容易算,例如下圖(a)。
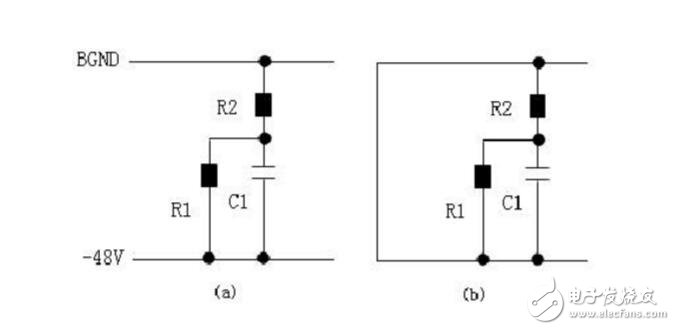
對于上圖(a),如果從充電的角度去計算時間常數會比較難,我們不妨換個角度來思考,我們知道,時間常數只與電阻和電容有關,而與電源無關,對于簡單的由一個電阻R和一個電容C串聯的電路來說,其充電和放電的時間參數是一樣的,都是RC,所以,我們可以把上圖中的電源短路,使電容C1放電,如上圖(b)所示,很容易得到其時間常數:
t = RC = (R1//R2)*C
使用同樣的方法,可以將下圖(a)電路等效成(b)的放電電路形式,得到電路的時間常數:
t = RC = R1*(C1+C2)
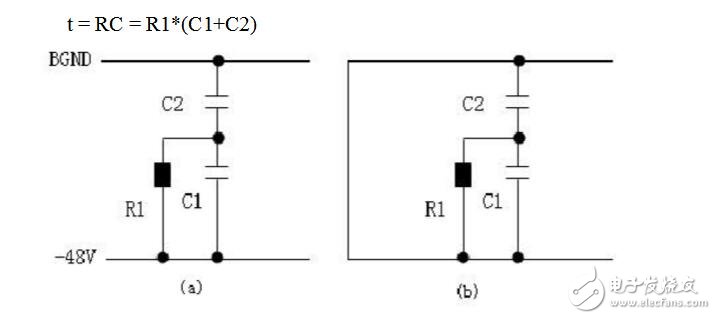
用同樣的方法,可以將下圖(a)電路等效成(b)的放電電路形式,得到電路的時間常數:
t = RC = ((R1//R3//R4)+R2)*C1
什么是截止頻率?
當保持輸入信號的幅度不變,改變頻率使輸出信號降至最大值的0.707倍,即用頻響特性來表述即為-3dB點處即為截止頻率,它是用來說明頻率特性指標的一個特殊頻率。
截止頻率的算法:
利用系統函數的模來表示電路的放大倍數,由于20lgA(ω)=-3dB,解得A(ω)=10^-0.15=0.707945784≈1/√2,又因為A(ω)=|H(jω)|,則|H(jω)|^2=1/2在高頻端和低頻端各有一個截止頻率,分別稱為上截止頻率和下截止頻率。兩個截止頻率之間的頻率范圍稱為通頻帶。
RC的時間常數和截止頻率的關系:
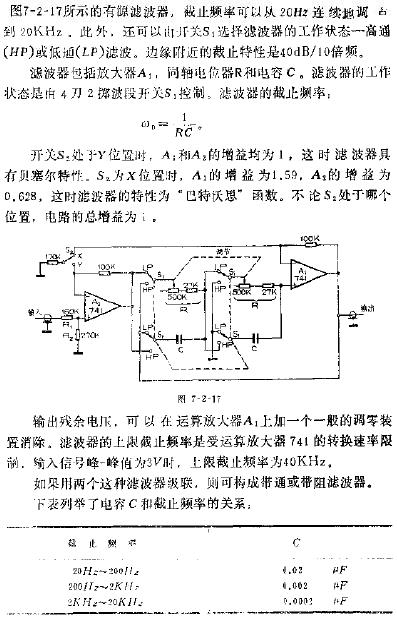
時間常數t = RC,截止頻率f = 1/2 π RC。在無源濾波器輸入端的RC,他的截止頻率是1/2 π RC,RC越大,他的截止頻率越小,同理他的時間常數也越大,則充放電時間也越長。
其次,時間常數和截止頻率是從不同方面分析RC充電電路所用的描述量。當我們從時域角度分析RC電路,我們會用RC充電常數。當我們從頻域角度分析RC電路(即RC濾波器),我們會用截止頻率。當輸入量的頻率等于截止頻率時,輸出與輸入的幅值之比為0.707,即增益為-3dB。
 電子發燒友App
電子發燒友App








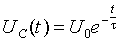
















評論