在計數體制中,通常用的是十進制,它有0,1,2,3,…,9十個數碼,用它們來組成一個數。但在數字電路中,為了把電路的兩個狀態(1態和0態)和數碼對應起來,采用二進制較為方便,二進制只有0和1兩個數碼。
十進制是以10為底數的計數體制,例如
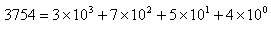
二進制是以2為底數的計數體制,例如
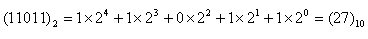
二進制數11011相當于十進制數27。
二進制加法器是數字電路的基本部件之一。二進制加法運算同邏輯加法運算的含義是不同的。前者是數的運算,而后者表示邏輯關系。二進制加法是“逢二進一”,即1+1=10,而邏輯加則為1+1=1。
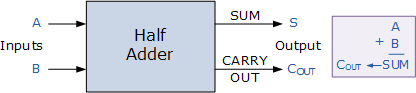
1、半加器
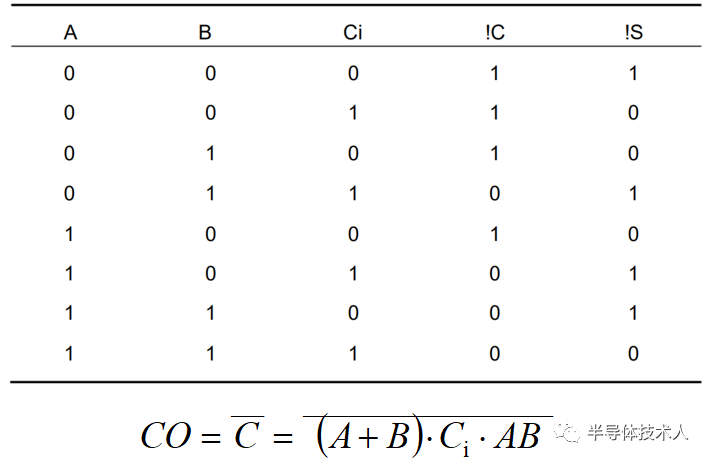
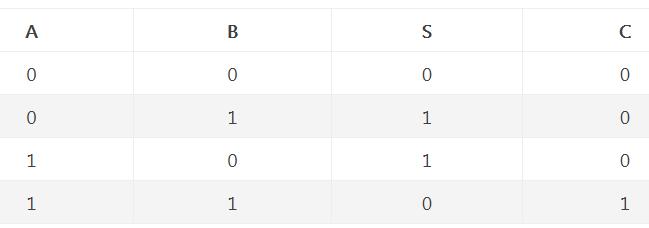
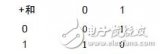
所謂“半加”,就是只求本位的和,暫不管低位送來的進位數。半加器的邏輯狀態表見表1。
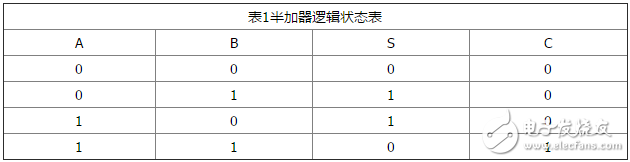
其中,A和B是相加的兩個數,S是半加和數,C是進位數。
由邏輯狀態表可寫出邏輯式:
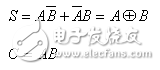
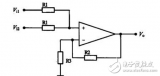
并由此畫出圖1(a)的邏輯圖。圖1(b)是半加器的邏輯符號。
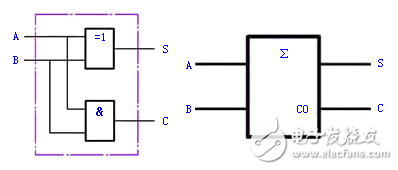
(a)邏輯圖(b)邏輯符號
圖1半加器邏輯圖及其邏輯符號
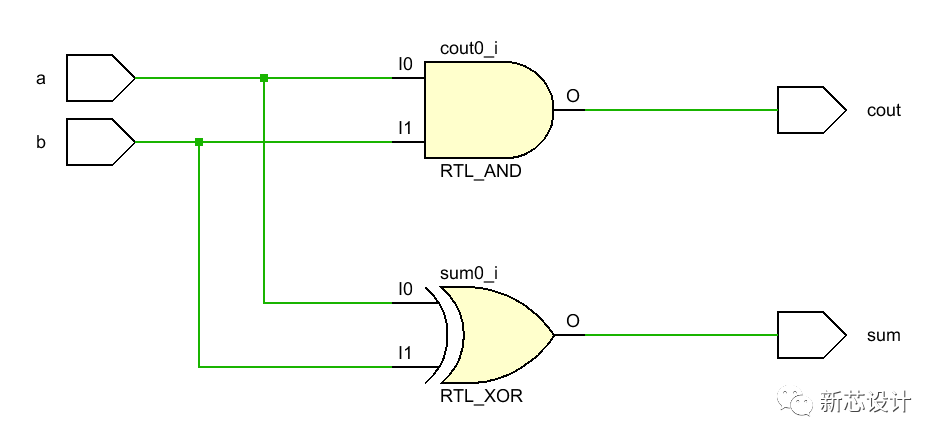
2、全加器
當多位數相加時,半加器可用于最低位求和,并給出進位數。第二位的相加有兩個待加數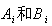 ,還有一個來自低位送來的進位數
,還有一個來自低位送來的進位數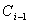 。這三個數相加,得出本位和數(全加和數)
。這三個數相加,得出本位和數(全加和數)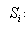 和進位數
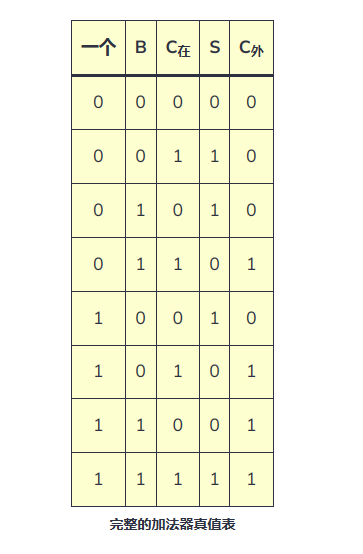
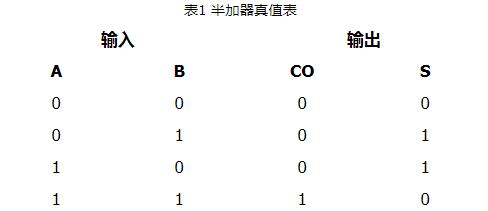
和進位數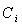 ,這就是“全加”,表2是全加器的邏輯狀態表
,這就是“全加”,表2是全加器的邏輯狀態表
表2全加器邏輯狀態圖
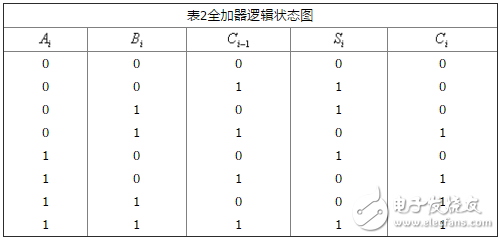
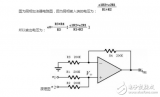
全加器可用兩個半加器和一個或門組成,如圖2(a)所示。![]() 在第一個半加器中相加,得出的結果再和
在第一個半加器中相加,得出的結果再和![]() 在第二個半加器中相加,即得出全加和
在第二個半加器中相加,即得出全加和![]() 。兩個半加器的進位數通過或門輸出作為本位的進位數
。兩個半加器的進位數通過或門輸出作為本位的進位數![]() 。圖2(b)是全加器的邏輯符號。
。圖2(b)是全加器的邏輯符號。
(a)邏輯圖(b)邏輯符號
圖2 全加器邏輯圖及其邏輯符號
例1、用4個全加器組成一個邏輯電路以實現兩個4位的二進制數A—1101(十進制為13)和B—1011(十進制為11)的加法運算。
解:
邏輯電路如圖3所示,和數是S—11000(十進制數為24)。根據全加器的邏輯狀態表自行分析。
這種全加器的任意一位的加法運算,都必須等到低位加法完成送來進位時才能進行。這種進位方式稱為串行進位,它的缺點是運算速度慢,但其電路比較簡單,因此在對運算速度要求不高的設備中,仍不失為一種可取的全加器。T692集成加法器就是這種串行加法器。
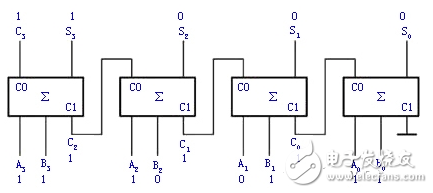
圖3 例1的邏輯圖
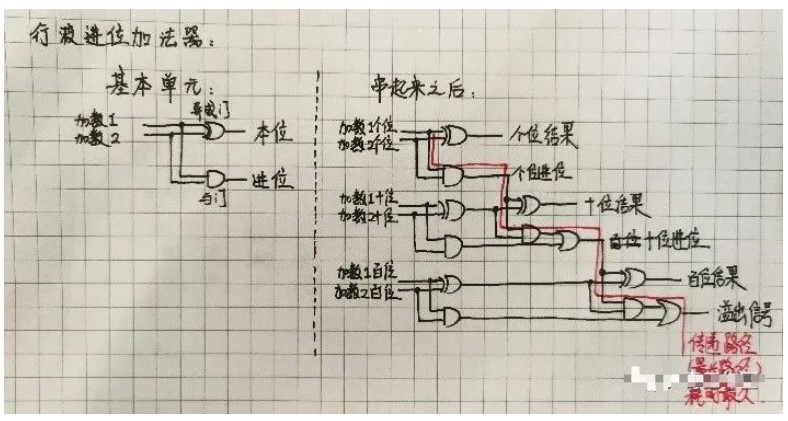
二進制加法器
一、多位二進制加法器
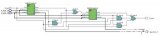
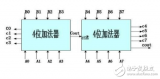
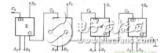
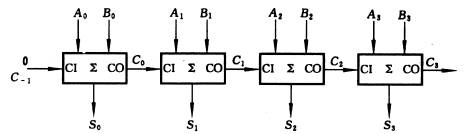
多位二進制加法電路種類很多,如四位并行輸入串行進位加法電路,如圖所示:
這種加法運算的速度是比較低的,在最不利的情況下,每做一次加法運算,需要經過4個全加器的傳輸延遲時間,才能得到穩定可靠的運算結果。
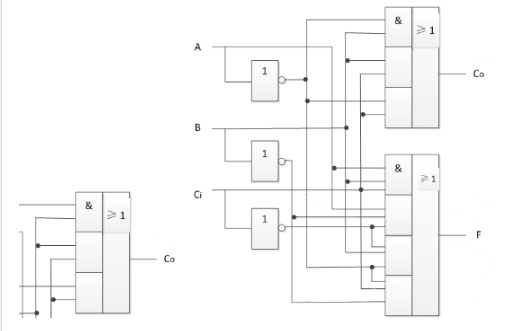
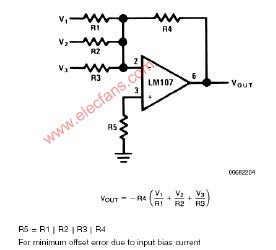
二、中規模集成超前進位加法器
為提高運算速度,必須設法減小或消除由于進位信號逐級傳遞所消耗的時間。那么高的進位輸入信號能否在相加運算開始時就知道呢?因為第i位的進位輸入信號![]() 是兩個加數中第i-1位以下各位數據的函數,即有:
是兩個加數中第i-1位以下各位數據的函數,即有:

 電子發燒友App
電子發燒友App










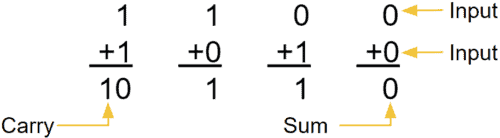
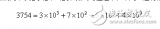











評論