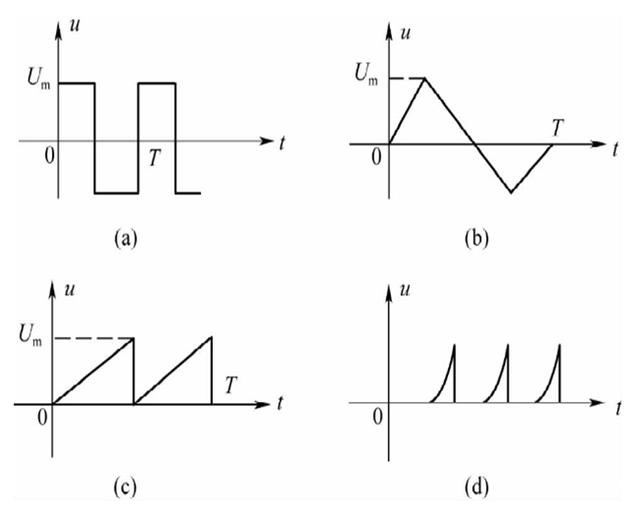
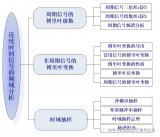
對于非正弦周期信號激勵的穩態電路,無法用直流電路或正弦交流電路的計算方法來分析計算,而必須先把非正弦周期信號激勵用傅里葉級數分解為不同頻率的正弦分量之和,然后再分別計算各個頻率分量激勵下的電路響應。最后用疊加定理把各響應分量進行疊加獲得穩態響應。其計算過程的主要步驟可分為三步:
(1)把給定的非正弦周期激勵源分解為傅里葉級數表達式,即分解為直流分量與各次諧波分量之和,根據展開式各項收斂性及所需精度確定所需諧波項數;
(2)分別計算直流分量和各頻率諧波分量激勵下的電路響應。直流分量用直流電路分析方法,此時電感短路、電容開路;對于不同頻率的正弦分量,采用正弦電路相量分析計算方法,這時需注意電路的阻抗隨頻率而變化,各分量單獨計算時應作出對應電路圖;
(3)應用疊加定理把輸出響應的各諧波分量相加得到總的響應值,注意疊加前應把各諧波響應表達成時域瞬時式(因為不同頻率的相量式相加是無意義的)。
下面用具體例子來說明線性電路的周期非正弦穩態分析。
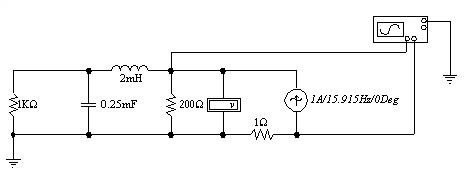
例6-2-1?? 電路如圖6-2-1所示,已知![]() ,
,![]() ,
,![]() ,電源電壓,基波角頻率
,電源電壓,基波角頻率![]() ,試求流過電阻的電流
,試求流過電阻的電流![]() 及電感兩端電壓
及電感兩端電壓![]() 。
。
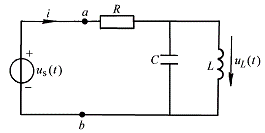
圖 6-2-1
解:本題的激勵電壓源已分解成各次諧波分量,因此可直接進行各次諧波的計算。對于直流分量的計算,可用一般直流電路的解題方法,畫出對應直流電路如圖6-2-2a所示,已知![]() ,則得
,則得
![]()
![]()
對于基波分量![]() ,其對應電路如圖6-2-2b所示,
,其對應電路如圖6-2-2b所示,![]() ,ab端入端阻抗:
,ab端入端阻抗:
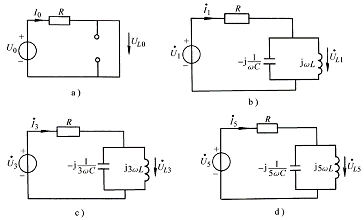
圖 6-2-2
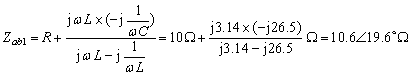
![]()
電感兩端電壓:
![]()
即有:
![]() ,
,![]()
對于三次諧波分量,其等效電路如圖6-2-2c所示,![]() ,其入端阻抗為:
,其入端阻抗為:
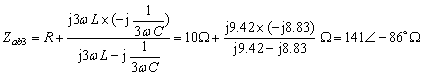
![]()
電感兩端電壓:
![]()
即有:
![]() ,
,![]()
對于五次諧波,等效電路如圖6-2-2d所示,有![]() ,ab端入端阻抗為:
,ab端入端阻抗為:

![]()
![]()
電感兩端電壓:
![]()
即有:
![]() ,
,![]()
最后得到流經電阻的電流值為:
![]()
![]()
![]()
![]()
![]()
![]()
從計算結果可看出,電路對不同頻率的分量呈現不同的特性。當三次諧波激勵時,入端阻抗特別大,因此產生的電流分量較小,這是由于接近電路諧振頻率點的緣故。
下面討論非正弦周期信號的有效值和功率問題。前面已定義了周期信號的有效值為:
![]()
對于非正弦周期信號電流![]() ,可展為傅里葉級數:
,可展為傅里葉級數:
![]()
代入有效值表達式有:
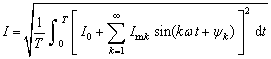
把根號內的平方展開,可得兩類表達式,一類是同頻率電流分量的平方,可計算得:
![]()
![]()
![]()
第二類為不同頻率的電流乘積,由三角函數的正交性可知,不同頻率的二個正弦函數乘積在![]() 上積分為零,即有:
上積分為零,即有:
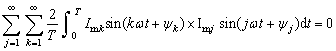 ???????
??????? ![]()
于是可得周期非正弦交流電流的有效值為:
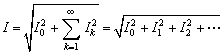 ???????????????? (6-2-1)
???????????????? (6-2-1)
式中,Ik為各次諧波的有效值。同理可推得非正弦周期電壓有效值為:
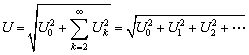 ???????????? (6-2-2)
???????????? (6-2-2)
?
非正弦周期信號的功率:
![]() ,
,
?式中,
![]() ,
,![]()
平均功率為:
![]()
將![]() 、
、![]() 展開式代入,其乘積的表達式由同頻率正弦量與不同頻率正弦量乘積組成,考慮到三角函數在
展開式代入,其乘積的表達式由同頻率正弦量與不同頻率正弦量乘積組成,考慮到三角函數在![]() 上的正交性,可推得:
上的正交性,可推得:
![]()
![]() ??? ??(6-2-3)
??? ??(6-2-3)
式中,![]() 為k次諧波電壓與電流相位差。由式可知,非正弦信號的平均功率等于各諧波信號平均功率之和。
為k次諧波電壓與電流相位差。由式可知,非正弦信號的平均功率等于各諧波信號平均功率之和。
 電子發燒友App
電子發燒友App


















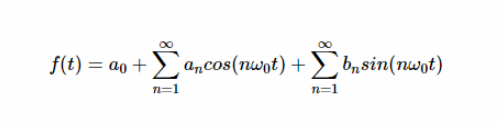













評論