0 引言
四旋翼飛行器是一種能夠實現垂直起降、懸停、偏航等復雜動作的多旋翼無人機,因而在軍事和民用領域的應用前景十分樂觀[1],但其自身系統的復雜性以及易受外界空氣動力和不確定因素影響的問題一直困擾著科研人員。
針對上述問題,科研人員對四旋翼飛行器系統模型的控制方法和濾波算法進行了研究。經典PID算法是一種不依賴于系統模型的控制方法,該方法結構簡單,理論成熟[2],但參數整定比較繁瑣。文獻[3-4]中反步法雖然對非線性系統有很好的跟蹤效果且反應速度快,但是其魯棒性差,抗干擾能力弱,且需要建立精確的系統模型。文獻[5]用滑膜控制法對四旋翼飛行器進行控制,雖然滑膜控制相對反步法具有較好的魯棒性,但此類算法都沒有對系統的干擾進行實時估計和補償,也沒有對各個通道進行解耦處理,當外界干擾較大時,其控制效果并不理想。控制方法的選取雖然可以減小對四旋翼模型的依賴性,保證內部系統的相對穩定,但要想實現四旋翼飛行器在復雜的環境中安全飛行,濾波算法的研究也是不可或缺的。
文獻[6]利用粒子濾波對飛行器姿態進行估計,其在非線性系統中表現出較強的優越性,但其計算量較大,難以滿足四旋翼飛行器實時控制的效果。文獻[7]利用互補濾波對四旋翼飛行器數據進行融合,該算法根據陀螺儀和加速度計傳感器特性的不同,將兩者的優點融合起來得到較好的數據,但其和粒子濾波一樣也存在系統延遲問題。文獻[8-9]提出基于卡爾曼濾波的姿態估計算法,其能夠有效地濾除外界噪聲,確保獲取數據的精度,但當系統濾波偏差較大時會出現濾波發散的現象,從而導致系統不能正常工作。
綜合以上問題,本文提出改進EKF的自抗擾控制方法,利用自抗擾控制器對飛行器姿態進行控制,將受噪聲干擾的姿態經改進EKF進行濾波,使得飛行姿態更加穩定,有效提高了系統的穩定性和抗干擾性。
1 四旋翼飛行器動力學模型
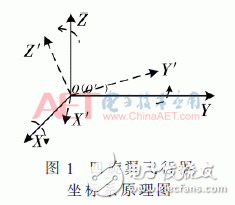
為得到四旋翼飛行器的數學模型,首先建立兩個坐標系:慣性坐標系E(OXYZ)和機體坐標系B(OX′Y′Z′)。其重心和質心均與飛行器原點O(O′)重合,如圖1所示。
則四旋翼的動力學模型為[10]:

由上式可知,四旋翼飛行器是一個欠驅動、非線性、強耦合系統。本文采用自抗擾控制器作為控制系統,同時利用改進EKF對帶有噪聲的飛行器姿態進行修正,其控制系統模型如圖2所示。
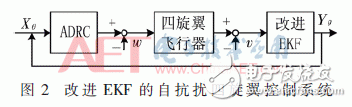
2 ADRC系統
2.1 ADRC系統結構
自抗擾控制是通過跟蹤微分器(TD)安排過渡過程,利用擴張觀測器(ESO)實現狀態間耦合項的跟蹤和估計,同時對系統總擾動進行估計,并根據擾動估計值采用非線性狀態誤差反饋(NLSEF)進行實時補償。其二階的結構如圖3所示[11]。
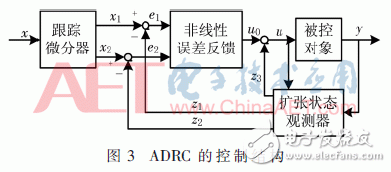
2.2 姿態控制系統的自抗擾解耦控制
四旋翼姿態子系統方程如下:

式中,b1、b2為控制器增益。
自抗擾控制器品質的好壞和其內部各模塊參數的整定有關,因此,對自抗擾控制器各模塊參數的整定是必要的。
2.3 自抗擾解耦控制參數的整定
因為ADRC中各模塊互不影響,因此,可以對各模塊的參數單獨整定,最后進行總體調整。
2.3.1 TD參數整定
跟蹤微分器中的速度因子r影響著跟蹤信號的速度,其影響效果如圖4所示。其中T=0.01,x=5是初始信號,y是跟蹤波形,分別對應著速度因子r=1、5、14的曲線。
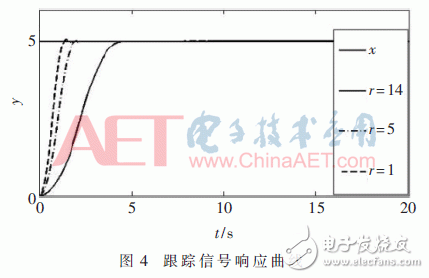
由圖4可知,速度因子r越大,跟蹤速度越快,容易造成超調現象,失去了微分跟蹤器的意義;r越小跟蹤過程越長,系統的實時性變差。
2.3.2 ESO參數整定
ESO是自抗擾控制器最重要的部分,一般選取a1=0.5,a2=0.25。σ是fal函數原點附近線性區間的寬度,若σ過大則可能無法準確跟蹤一些非線性信號,大大降低了ADRC的控制效果;σ太小則會在原點位附近出現信號跳變現象,降低了系統的穩定性。而β1、β2、β3僅影響ESO的收斂速度,不因控制對象的改變而改變[12]。
2.3.3 NLSEF參數整定
NLSEF中控制量增益b1、b2對控制效果的影響較大。控制量增益大會導致系統發散,影響系統的安全性;控制增益越小,則系統的實時性較差,故應根據不同的控制系統動態調整。
3 改進EKF濾波原理及算法
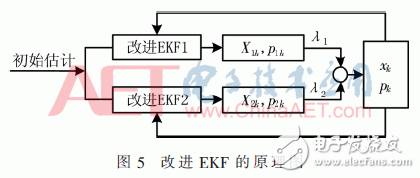
本文提出一種改進的EKF算法,首先,計算觀測矩陣時進行迭代處理以提高濾波精度。然后,采用兩個迭代的EKF對四旋翼飛行器的姿態數據進行預測和更新,將它們輸出的狀態變量加權整合后輸出飛行器的最優狀態估計,其原理圖如圖5所示。
對于一個離散隨機系統: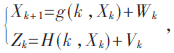 其中Wk、Vk分別為系統k時刻的過程噪聲和觀測噪聲且均為均值為零的高斯白噪聲,對應的方差分別為Qk、Wk。改進EKF算法過程如下:
其中Wk、Vk分別為系統k時刻的過程噪聲和觀測噪聲且均為均值為零的高斯白噪聲,對應的方差分別為Qk、Wk。改進EKF算法過程如下:
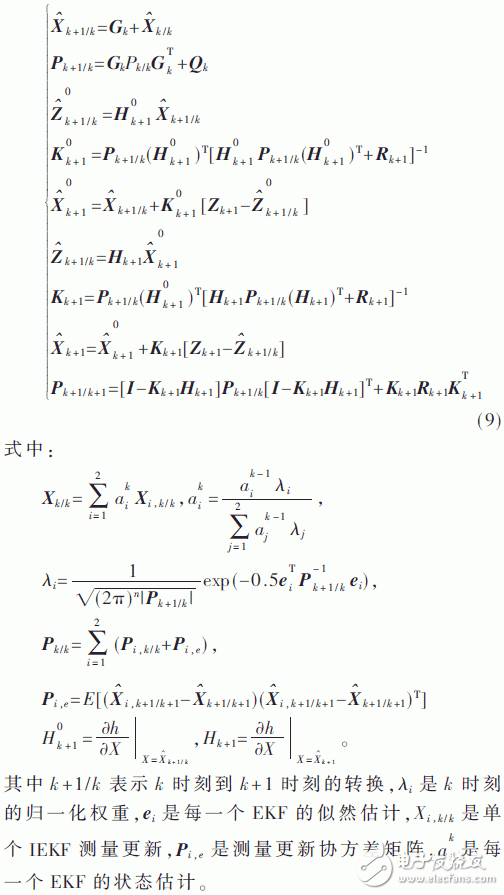
4 仿真與實驗結果分析
本文在前期的工作中已完成了雙環PID、改進EKF的自抗擾飛控系統的仿真和實驗,飛行器在改進EKF的自抗擾控制器控制下的實際飛行效果如圖6所示。

4.1 改進EKF的自抗擾穩定性控制實驗
為了驗證該方法對四旋翼飛行器穩定性控制的效果,給定飛行器橫滾角的期望值為θ=20°,其仿真結果如圖7所示。
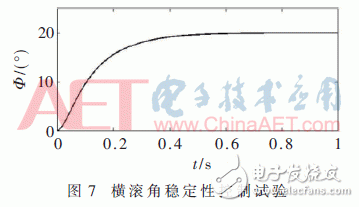
由圖7可知,俯仰角可以在0.9 s左右達到期望值,且狀態調整過程中沒有出現任何振蕩,可以看出該控制方式對飛行器穩定性控制效果十分理想。
4.2 改進EKF的自抗擾和串級PID對比實驗
給定橫滾角的初始值均為0°,且信號是周期性變化的方波,其中橫滾通道方波增益為φ=15°。在改進EKF的自抗擾和串級PID控制下的系統輸出曲線如圖8所示。
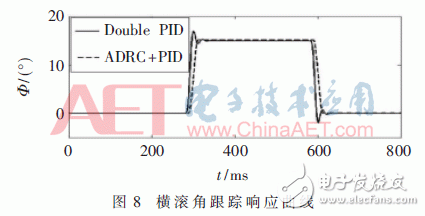
由圖8可知,兩種控制方式對橫滾角都有很好的跟蹤效果,但串級PID控制器的姿態角響應曲線會產生震蕩現象,而改進的EKF的自抗擾控制則無此現象。
4.3 高度控制對比實驗
給定四旋翼飛行器初始高度為0 m,期望高度為2 m,其在改進EKF的自抗擾和串級PID控制下的系統輸出如圖9所示。
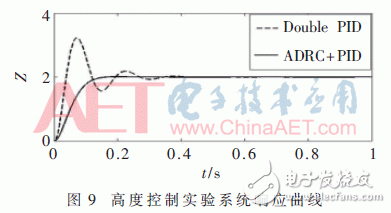
由圖9可知,在期望值2 m條件下,串級PID控制的超調量在50%以上,穩定時間在0.9 s左右,而改進EKF的自抗擾控制曲線超調量在5%以下,穩定時間大約在0.5 s左右。
4.4 改進EKF的ADRC、ADRC、串級PID抗干擾性對比實驗
四旋翼實際飛行時,系統會受到傳感器噪聲干擾和外部突變的影響,為了模擬傳感器噪聲干擾,實驗對橫滾角的反饋變量加入了高斯白噪聲;為了模擬外部突變的影響,在200 ms時刻對橫滾角回路的角加速度加入幅值是20、脈寬為100 ms的矩形波作為突變信號來檢測控制器的抗干擾性能,仿真結果如圖10所示。
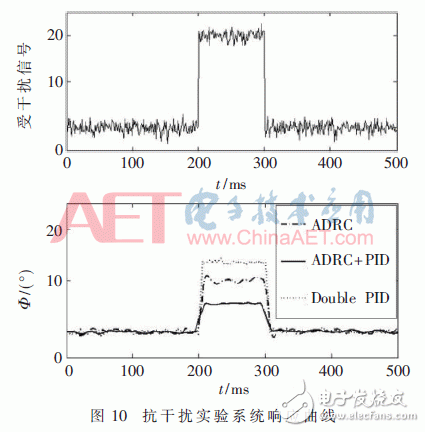
由圖10可知,同等條件下,改進EKF的自抗擾控制器抗干擾效果更加的突出。
4.5 飛行器實際飛行橫滾角、高度曲線
實際飛行時,給定橫滾角幅值為12左右的突變信號,給定高度的幅值大約是8。利用數傳把數據傳到電腦上,其在上位機上的曲線分別如圖11所示。
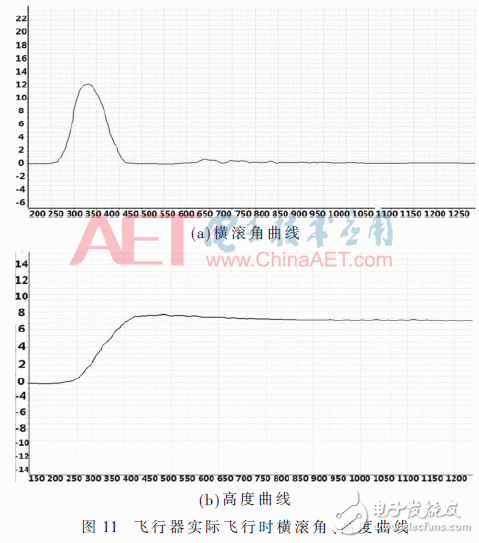
由圖11可知,在改進EKF的自抗擾控制器下的四旋翼飛行器,其可以快速實現姿態角的恢復及高度的控制,實現飛行器穩定的飛行。
5 結論
實驗結果表明,該方法控制下,飛行器可以從50°橫滾角的情況下迅速恢復到平衡,且高度控制、抗干擾能力較之串級PID控制反應更加迅速,平穩。在接下來的工作中,會對四旋翼飛行器的避障和路徑規劃進行研究,利用超聲波測量四旋翼與障礙物之間的距離,采用單目視覺對飛行器進行定位,最終實現四旋翼飛行器自主飛行。
-
無人機
+關注
關注
230文章
10512瀏覽量
181711
發布評論請先 登錄
相關推薦
自抗擾pH控制方法及其應用研究
自適應模糊自抗擾控制器的研究與設計
進行自適應模糊自抗擾控制器的研究與設計資料說明
永磁同步電機自抗擾伺服控制算法仿真模型研究





 關于改進EKF的自抗擾飛控系統的設計
關于改進EKF的自抗擾飛控系統的設計











評論