本篇主要涉及到圖論的基本算法,不包含有關最大流的內容。圖論的大部分算法都是由性質或推論得出來的,想樸素想出來確實不容易。
一個圖的所有頂點可以劃分成兩個子集,使所有的邊的入度和出度頂點分別在這兩個子集中。
這個問題可以轉換為上篇提到過的圖的著色問題,只要看圖是否能著2個顏色就行了。當然,可以回溯解決這個問題,不過對于著2個顏色可以BFS解決。
同樣,一維數組colors表示節點已著的顏色。
偽代碼:
IS-BIPARTITE(g,colors)
let queue be new Queue
colors[0] = 1
queue.push(0)
while queue.empty() == false
let v = queue.top()
queue.pop()
for i equal to every vertex in g
if colors[i] == 0
colors[i] = 3 - colors[v]
queue.push(i)
else if colors[i] == colors[v]
return false
end
end
return true
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
DFS改良(DFS-Improve)
上篇文章提到過,搜索解空間是樹形的,也就是在說BFS和DFS。那么在對圖進行BFS和DFS有什么區別呢,這個問題要從解空間角度去理解。對圖進行BFS的解空間是一顆樹,可叫廣度優先樹。而DFS是多棵樹構成的森林,可叫深度優先森林。
這里要對DFS進行小小的改良,它的性質會對解多個問題會很有幫助。原版DFS搜索的時候,會先遍歷本頂點,再遞歸遍歷臨接的頂點。DFS改良希望能先遞歸遍歷臨接的頂點,再遍歷本頂點,并且按遍歷順序逆序存儲起來。
偽代碼:
DFS-IMPROVE(v,visited,stack)
visited[v] = true
for i equal to every vertex adjacent to v
if visited[i] == false
DFS-IMPROVE(i,visited,stack)
end
stack.push(v)
這個改良版DFS有個很有用的性質就是,對于兩個頂點A、B,存在A到B的路徑,而不存在B到A的路徑,則從記錄的順序中取出的時候,一定會先取出頂點A,再取出頂點B。以下為這個性質的證明。
假設:有兩個頂點A和B,存在路徑從A到B,不存在路徑從B到A。
證明:分為兩種情況,情況一,先搜索到A頂點,情況二,先搜索到B頂點。對于情況一,由命題可得,A一定存儲在B之后,那么取出時先取出的是頂點A。對于情況二,先搜索到B頂點,由于B頂點搜索不到A頂點,則A一定存儲在B之后,那么取出時仍先取出的是頂點A,命題得證。
DFS改良性質:對于兩個頂點A、B,存在A到B的路徑,而不存在B到A的路徑,則從記錄的順序中取出的時候,一定會先取出頂點A,再取出頂點B。
歐拉回路(Eulerian-Path-And-Circuit)
在無向圖中,歐拉路徑定義為,一條路徑經過所有的邊,每個邊只經過一次。歐拉回路定義為,存在一條歐拉路徑且路徑的起點和終點為同一個頂點。可以看到只有連通圖才能有歐拉回路和歐拉路徑。
這個算法很巧。如果一條路徑要經過一個頂點,本質是從一條邊到達一個頂點,然后從這個頂點通過另一條邊出去。歐拉回路就是要求路徑要經過所有的點,起點和終點還都是同一個頂點。那么就等價于要求所有頂點連接的邊是2個。實際上,路徑還可以經過頂點多次,那么就等價于要求所有頂點連接的邊是偶數個。歐拉路徑的要求就等價于所有頂點連接的邊是偶數個,除了起點和終點兩個頂點可以是奇數個。
先判斷圖是否是連通圖。返回0代表沒有歐拉回路或者歐拉路徑,返回1代表有歐拉路徑,返回2代表有歐拉回路。
偽代碼:
EULERIAN-PATH-AND-CIRCUIT(g)
if isConnected(g) == false
return 0
let odd = 0
for v equal to every vertex in g
if v has not even edge
odd = odd + 1
end
if odd > 2
returon 0
if odd == 1
return 1
if odd == 0
return 2
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
拓撲排序(Topological-Sorting)
將一張有向無環圖的頂點排序,排序規則是所有邊的入度頂點要在出度頂點之前。可以看到,無向和有環圖都不存在拓撲排序,并且拓撲排序可能存在多種解。
拓撲排序有兩種解法,一種是從搜索角度。
如果我能保障先遞歸遍歷臨接的頂點,再遍歷本頂點的話,那么遍歷的順序的逆序就是一個拓撲排序。那么就可以直接用DFS改良求解出拓撲排序。
偽代碼:
TOPOLOGICAL-SORTING-DFS(g)
let visited be new Array
let result be new Array
let stack be new Stack
for v equal to every vertex in g
if visited[v] == false
DFS-IMPROVE(v,visited,stack)
end
while stack.empty() == false
result.append(stack.top())
stack.pop()
end
return result
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
另一種是貪心選擇。
直覺上,既然要所有邊的出度頂點在入度頂點之前,可以從入度和出度角度來解決問題。可以讓入度最小的排序在前,也可以讓出度最大的排序在后,排序后,這個頂點的邊都不會再影響問題了,可以去掉。去掉后再重新加入新的頂點,直到加入所有頂點。
這個問題還有個隱含條件,挑選出、入度最小的頂點就等價于挑選出、入度為0的頂點。這是因為圖必須是無環圖,所以肯定存在出、入度為0的頂點,那么出、入度最小的頂點就是出、入度為0的頂點。
直覺上這是一個可行的策略,細想一下,按出度最大排序和按入度為零排序是否等價。實際上是不等價的,按入度為零排序,如果出現了多個入度為零的頂點,這多個頂點排序的順序是無關的,可以任意排序。而按出度最大排序,出現了多個入度最大的頂點,這多個頂點排序是有關的,不能任意排序。所以,只能按入度為零排序。實際上,這個想法就是貪心選擇。下面以挑選入度為零的邊作為貪心選擇解決問題,同樣地,還是先證明這個貪心選擇的正確性。
命題:入度為零的頂點v排序在前。
假設:S為圖的一個拓撲排序,l為此排序的首個頂點。
證明:如果l=v,則命題得證。如果l不等于v,將l頂點從S中去除,然后加入頂點v得到新的排序S‘。因為S去除l以后l以后的排序沒有變,仍為拓撲排序,v入度為零,v前面可以沒有頂點,所以S’也為圖的一個拓撲排序,命題得證。
偽代碼:
TOPOLOGICAL-SORTING-GREEDY(g)
let inDegree be every verties inDegree Array
let stack be new Stack
let result be new Array
for v equal to every vertex in g
if inDegree[v] == 0
stack.push(v)
end
while stack.empty() == false
vertex v = stack.top()
stack.pop()
result.append(v)
for i equal to every vertex adjacent to v
inDegree[i] = inDegree[i] - 1
if inDegree[i] == 0
stack.push(i)
end
end
return result.reverse()
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
強連通分量(Strongly-Connected-Components)
圖中的一個頂點與另一個頂點互相都有路徑可以抵達,就說這兩個頂點強連通。圖中有多個頂點兩兩之間都強連通,則這多個頂點構成圖的強連通分量。
樸素的想法是,假如從一個頂點A可以搜索到另一個頂點B,如果從B頂點再能搜索回A頂點的話,A、B就在一個強連通分量中。不過,這樣每兩個頂點要進行兩次DFS,復雜度肯定會很高。這里可以引入轉置圖(將有向邊的方向翻轉)的性質。這樣問題就轉換成了,從A頂點搜索到B頂點,將圖轉置后,如果再A頂點還能搜索到B頂點,A、B頂點就在一個強連通分量中。用算法表述出來就是先從A頂點DFS,然后將圖轉置,再從A頂點DFS,兩次DFS都能搜索到B頂點的話,B頂點就與A頂點在同一個強連通分量中。然而樸素想法只能想到這里了。
有多個算法被研究出來解決這個問題,下面先介紹Kosaraju算法。
Kosaraju
Kosaraju算法使用了DFS改良的性質去解決問題,想法很有趣。Kosaraju算法現將圖進行DFS改良,然后將圖轉置,再進行DFS。第二次DFS每個頂點能夠搜索到的點就是一個強連通分量。算法正確性和說明如下。
通過DFS改良性質可以得出定理,一個強連通分量C如果有到達另一個強連通分量C’的路徑,則C’比C先被搜索完,這個定理很明顯,如果C中有路徑到C’,那么根據DFS改良性質一定會先搜索到C,再搜索完C’,再搜索完C。將這個定理做定理1。
定理1:一個強連通分量C如果有到達另一個強連通分量C’的路徑,則C’比C先被搜索完。
定理1還可以再進行推論,如果一個強連通分量C有到達另一個強連通分量C’的路徑,則將圖轉置后,C比C’先被搜索完,這個推論也很明顯,將圖轉置后,不存在C到C’的路徑,存在C’到C的路徑,而仍是先搜索C再搜索C‘,所以C比C‘先被搜索完,這個推論作為推論1。
推論1:如果一個強連通分量C有到達另一個強連通分量C’的路徑,則將圖轉置后,C比C’先被搜索完。

以下為用結構歸納法對算法正確性進行證明。
命題:第二次DFS每個頂點能夠搜索到的點就是一個強連通分量。
假設:n代表圖中有多少個強連通分量。
證明:如果n=1,則第二次DFS就是搜索一遍所有頂點,命題得證。現在假設n=k時,命題成立。現證明n=k+1時,是否成立。假設搜索到第k+1個強連通分量的第一個頂點為u,u肯定能搜索到所有k+1個強連通分量的頂點。并且根據推論1,此時被轉置后的圖,所有從第k+1個強連通分量能到達的其他強連通分量都已經被搜索過了。所以u只能搜索到所有第k+1個強連通分量的頂點,即第二次DFS每個頂點只能夠搜索到包含此頂點的強連通分量中的頂點,命題得證。
偽代碼:
KOSARAJU-STRONGLY-CONNECTED-COMPONENTS(g)
let visited be new Array
let stack be new Stack
for v equal to every vertex in g
if visited[v] == false
DFS-IMPROVE(v,visited,stack)
end
let gt = transpose of g
for v equal to every vertex in g
visited[v] = false
end
while stack.empty() == false
vertex v = stack.top()
stack.pop()
if visited[v] == false
DFS(v,visited)
print ' Found a Strongly Connected Components '
end
DFS(v,visited)
visited[v] = true
print v
for i equal to every vertex adjacent to v
if visited[i] == false
DFS(i,visited,stack)
end
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
Kosaraju算法需要進行兩次DFS,那么可不可以只進行一次DFS,邊遍歷邊找強連通分量?Tarjan就是這樣的算法。
Tarjan
同樣,還是要基于DFS搜索性質來思考問題。DFS創建出的深度優先搜索樹會先被訪問根節點再被訪問子孫節點。什么時候會出現強連通分量?只有子孫節點有連通祖先節點的邊的時候。如果從某個節點,其子孫節點都只有指向自己子孫節點的邊的時候,這是明顯沒有構成強連通分量的。那么,出現了子孫節點指向其祖先節點的時候,從被指向的祖先節點一直搜索到指向的子孫節點所經過所有頂點就構成了一個強連通分量。如果出現了多個子孫節點都指向了祖先節點怎么辦?最早被指向、訪問的祖先節點到最晚指向、訪問的子孫節點構成了“最大“的強連通分量,這才是想要找的強連通分量。如果遇到了一個指向祖先節點的子孫節點,就算構成一個強連通分量,會導致找到多個互相嵌套的強連通分量。那么,要記錄訪問順序就要為每個節點設置一個被訪問順序的編號,讓屬于同一個強連通分量的頂點編號一致。上面討論的是構成了一個強連通分量怎么處理,如果沒有多個節點構成的強連通分量怎么處理?在搜索節點之前,為這個節點默認設置上被訪問的順序編號,這樣如果沒有搜索到多個節點構成的強連通分量,每個節點就是自己的強連通分量。
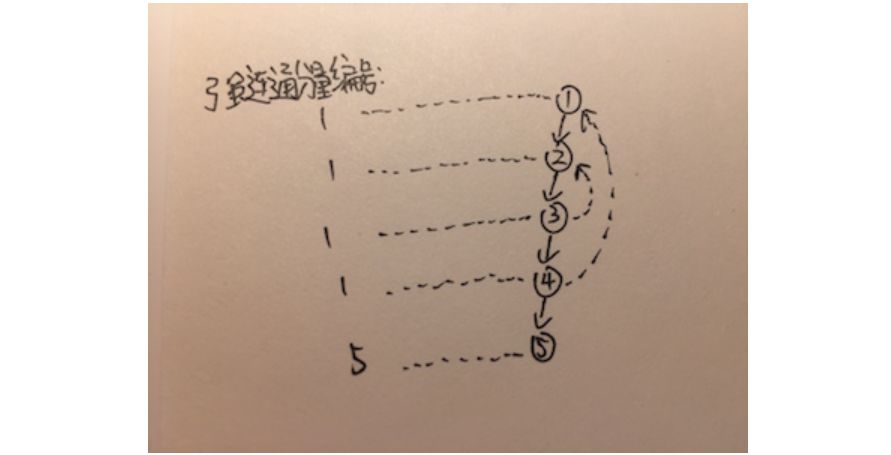
算法表述為,從某個節點開始搜索,默認設置自己為一個強連通分量。只要節點有子孫節點,就要等待子孫節點都搜索完,再更新自己強連通分量信息。只要節點有指向祖先節點,也要更新自己的強連通分量。判斷子孫節點構成的強連通分量”大“還是自己構成的強連通分量”大“,自己屬于最”大“的強連通分量。也就是說,算法找出了所有頂點的所屬的最“大”強連通分量。
數組disc表示頂點被訪問順序的編號,數組low表示頂點所在的強連通分量編號。最后當頂點在disc和low中編號一致時,代表頂點是所在強連通分量中第一個被搜索到的頂點。此時,輸出所在的強連通分量所包括的頂點。
偽代碼:
TARJAN-STRONGLY-CONNECTED-COMPONENTS(g)
let disc be new Array
let low be new Array
let stack be new Stack
let isInStack be new Array
for i from 1 to the number of vertex in g
disc [i] = -1
low [i] = -1
end
for u from 1 to the number of vertex in g
if disc[i] != -1
TARJAN-STRONGLY-CONNECTED-COMPONENTS-UTIL(u,disc,low,stack,isInStack)
end
TARJAN-STRONGLY-CONNECTED-COMPONENTS-UTIL(u,disc,low,stack,isInStack)
let time be static
time = time + 1
disc[u] = low[u] = time
stack.push(u)
isInStack[u] = true
for v equal to every vertex adjacent to u
if disc[v] == -1
TARJAN-STRONGLY-CONNECTED-COMPONENTS-UTIL(v,disc,low,stack,isInStack)
low[u] = min(low[u],low[v])
else if isInStack[v] == true
low[u] = min(low[u],disc[v])
end
let w = 0
if low[u] == disc[u]
while stack.top() != u
w = stack.top()
isInStack[w] = false
stack.pop()
print w
end
w = stack.top()
isInStack[w] = false
stack.pop()
print w
print ' Found a Strongly Connected Components '
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
圖的割點(Articulation Points)、橋(Bridge)、雙連通分量(Biconnected Components)
圖的割點(Articulation-Points)
圖的割點也叫圖的關節點,定義為無向圖中分割兩個連通分量的點,或者說去掉這個點,圖中的連通分量數增加了。可以看到如果求出了連通分量,那么不同連通分量中間的頂點就是割點。什么時候某個頂點不是這樣的割點?如果這個頂點的子孫頂點有連接這個頂點祖先頂點的邊,那么去掉這個頂點,這個頂點的子孫頂點和祖先頂點仍然連通。那么,尋找割點的過程就等價于尋找子孫頂點沒有連接祖先頂點的頂點。這個問題的求解過程類似于Tarjan強連通分量的求解過程。
不過,這個問題有個例外就是根頂點,對一般頂點的處理方式處理根頂點行得通嗎?根頂點肯定沒有子孫頂點指向祖先頂點,但是根頂點可以是割點。所以,根頂點需要特殊處理。根頂點什么時候是割點?當根頂點有多顆子樹,且之間無法互相到達的時候。那么,存不存在根頂點有多顆子樹,且之間可以互相到達?不存在,如果互相之間可以到達,那在根頂點搜索第一顆子樹的時候,就會搜索到可到達的子樹,就不會存在多顆子樹了。所以,根頂點有多顆子樹,那么這多顆子樹之間一定無法互相到達。根頂點有多顆子樹,且之間無法互相到達的時候就等價于根頂點有多顆子樹。所以,只要根頂點有多顆子樹,那么根頂點就是割點。
同樣地,數組disc表示頂點被訪問順序的編號,數組low表示頂點所在的強連通分量編號。數組parent找出根頂點。
偽代碼:
ARTICULATION-POINTS(g)
let disc be new Array
let low be new Array
let result be new Array
let parent be new Array
let visited be new Array
for i from 1 to the number of vertex in g
result [i] = false
visited [i] = false
parent [i] = -1
end
for u from 1 to the number of vertex in g
if visited[i] == false
ARTICULATION-POINTS-UTIL(u,disc,low,result,parent,visited)
end
for i from 1 to the number if vertex in g
if result[i] == true
print ' Found a Articulation Points i '
end
ARTICULATION-POINTS-UTIL(u,disc,low,result,parent,visited)
let time be static
time = time + 1
let children = 0
disc[u] = low[u] = time
visited[u] = true
for v equal to every vertex adjacent to u
if visited[v] == false
children = children + 1
parent[v] = u
ARTICULATION-POINTS-UTIL(u,disc,low,result,parent,visited)
low[u] = min(low[u],low[v])
if parnet[u] == -1 and children > 1
result[u] = true
if parent[u] != -1 and low[v] >= disc[u]
result[u] = true
else if v != parent[u]
low[u] = min(low[u],disc[v])
end
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
橋(Bridge)
橋定義為一條邊,且去掉這個邊,圖中的連通分量數增加了。類似于尋找割點,尋找橋就是尋找這樣一條,一端的頂點的子孫頂點沒有連接這個頂點和其祖先頂點的邊。求解過程和求割點基本一致。
偽代碼:
BRIDGE(g)
let disc be new Array
let low be new Array
let parent be new Array
let visited be new Array
for i from 1 to the number of vertex in g
visited [i] = false
parent [i] = -1
end
for u from 1 to the number of vertex in g
if visited[i] == false
BRIDGE-UTIL(u,disc,low,parent,visited)
end
BRIDGE-UTIL(u,disc,low,parent,visited)
let time be static
time = time + 1
disc[u] = low[u] = time
for v equal to every vertex adjacent to u
if visited[v] == false
parent[v] = u
BRIDGE-UTIL(u,disc,low,parent,visited)
low[u] = min(low[u],low[v])
if low[v] > disc[u]
print ' Found a Bridge u->v '
else if v != parent[u]
low[u] = min(low[u],disc[v])
end
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
雙連通分量(Biconnected-Components)
雙連通圖定義為沒有割點的圖。雙連通圖的極大子圖就為雙連通分量。雙連通分量就是在割點分割成多個連通分量處,共享割點。也就是說雙連通分量是去掉割點后構成的連通分量,加上割點和到達割點的邊。可以看出,雙連通分量可分為不含有割點、一個割點、兩個割點三種情況。對于不含有割點,說明圖為雙連通圖。對于含有一個割點,可能為初始搜索的頂點到第一個割點之間的邊構成的雙連通分量,可能為遇到一個割點后到不再遇到割點之間的邊構成雙連通分量。對于含有兩個割點,兩個割點之間的邊構成了一個雙連通分量。
求解此問題,只要在求割點的算法上做更改就可以了。按照求割點的算法求解割點,找到一個割點,輸出找到的邊,然后刪除找到的邊的記錄,再去搜索下一個割點。每搜索完圖某個頂點的可達頂點,輸出找到的邊。這樣就涵蓋了所有的情況。
偽代碼:
BICONNECTED-COMPONENTS(g)
let disc be new Array
let low be new Array
let stack be new Stack
let parent be new Array
for i from 1 to the number of vertex in g
disc [i] = -1
low [i] = -1
parent [i] = -1
end
for u from 1 to the number of vertex in g
if disc[i] == -1
BICONNECTED-COMPONENTS-UTIL(u,disc,low,stack,parent)
let flag = flase
while stack.empty() == false
flag = true
print stack.top().src -> stack.top().des
stack.pop()
end
if flag == true
print ' Found a Bioconnected-Components '
end
BICONNECTED-COMPONENTS-UTIL(u,disc,low,stack,parent)
let time be static
time = time + 1
let children = 0
disc[u] = low[u] = time
for v equal to every vertex adjacent to u
if disc[v] == -1
children = children + 1
parent[v] = u
stack.push(u->v)
BICONNECTED-COMPONENTS-UTIL(u,disc,low,stack,parent)
low[u] = min(low[u],low[v])
if (parnet[u] == -1 and children > 1) or (parent[u] != -1 and low[v] >= disc[u])
while stack.top().src != u or stack.top().des != v
print stack.top().src -> stack.top().des
stack.pop()
end
print stack.top().src -> stack.top().des
stack.pop()
print ' Found a Bioconnected-Components '
else if v != parent[u] and disc[v] < low[u]
low[u] = min(low[u],disc[v])
stack.push(u->v)
end
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
最小生成樹(Minimum-Spanning-Tree)
生成樹是指,在一個連通、無向、有權的圖中,所有頂點構成的一顆樹。圖中可以有多顆生成樹,而生成樹的代價就是樹中所有邊的權重的和。最小生成樹就是生成樹中代價最小的。
樸素的想法就是從圖中選擇最小權重的邊,直到生成一顆樹。看通用的算法之前,同樣要討論一下最小生成樹的性質。
對于一個連通、無向、有權圖中,一定有最小生成樹。如果圖不包含最小生成樹的任意一條邊,那么圖就是不連通的了,這與已知連通圖不符,所以圖必包含最小生成樹。
假設,A為某個最小生成樹的子集(任意一個頂點都是最小生成樹的子集)。
那么,為A一直添加對的邊,A最后就會成為一顆最小生成樹。那么最小生成樹問題就轉換成為了,一直找到對的邊,直到成為一顆最小生成樹。這個對的邊可以叫做安全邊。
安全邊如何尋找顯然就成了解決這個問題的關鍵點。
再假設,圖中所有頂點為V,將所有頂點切割成兩個部分S和V減去S。所有連接這兩個部分的邊,很形象的叫做橫跨切割,這些邊橫跨了兩個部分,成為這兩個部分的橋梁。這里還有個問題,如何切割?使A不包含橫跨切割。這樣的切割有多種切法,切割后,橫跨切割的最小代價邊就為A的安全邊。將這個作為定理1。

定理1:存在這樣一個將所有頂點分成兩個部分的切割,且使某個最小生成樹子集A不包含橫跨切割。則橫跨此切割的最小代價邊,就是A的安全邊。
以下為此定理的證明,這個定理的基礎實際上是連通性。
命題:橫跨切割的最小代價邊為A的安全邊。
假設:橫跨切割后的最小代價邊為x,有最小生成樹T包含A,但是不包含x。
證明:既然T不包含x,那么T必須包含另一條連接x兩端頂點的路徑,這條路徑上又必須有條邊橫跨切割。假設這條邊為y。T將y減去后,x兩端的頂點就無法互相到達。這時如果再加上x,那么x兩端的頂點又可以互相到達,并且構造了另一顆生成樹T’。可以看到,x的代價小于或等于y的代價,那么T‘的代價也小于或等于T的代價,那么T’也就是一顆最小生成樹。那么x既不在A中,x又在一顆包含A的最小生成樹中。命題得證。
可以看到這個證明過程使用的就是經常拿來證明貪心選擇的技巧,也就是說最小生成樹問題符合貪心算法的特征,也就解釋了為什么下面將要提到的兩個算法都是貪心算法。
定理1還可以進行推論,既然切割有多種方法,那可不可以對A和其余的頂點進行切割,設B為包括A和所有頂點構成的一個森林,C是其中的一個連通分量,那么C連接其他的連通分量的最小代價邊是A的安全邊。這個推論很好證明,因為A是B中的一個或者多個連通分量,如果按照C去切割圖分成C和B減去C,不可能切割A,即A中必定不包含橫跨切割。那么,橫跨這個切割的最小代價邊就是安全邊,即C連接其他連通分量的最小代價邊,推論成立。將這個推論作為推論1。
推論1:某個最小生成樹子集A和其他頂點構成的森林中,任意一個連通分量連接其他連通分量的最小代價邊都為A的安全邊。
如果從所有不在A中的邊選擇最小代價的邊,這個邊一定連接著某個連通分量,這個推論也就將選安全邊的范圍拓展到任意一條不在A中的邊。這個推論正好可以證明樸素想法的正確性。
接下來看一下最小生成樹的三個通用的算法Kruskal、Prime、Boruvka。
Kruskal
樸素想法和Kruskal已經很接近了。Kruskal算法做的就是一直選擇代價最小的邊,不過,如果選擇這個邊后,無生成最小生成樹,而生成圖了怎么辦?Kruskal比樸素想法巧的地方就是不選擇會成環的邊。
Kruskal常用的檢查是否成環的數據結構是UnionFind(并查集),UnionFind有個操作,一個是Find檢查元素所在集合的編號,Union將兩個元素合并成一個集合。
KRUSKAL(g)
let edges be all the edges of g
sort(edges)
let uf be new UnionFind
let e = 0
let i = 0
let result be new Array
while e < edges.length()
let edge = edges[i]
i = i + 1
if uf.find(edge.src) != uf.find(edge.des)
result.append(edge)
e = e + 1
uf.union(edge.src,edge.des)
end
return result
V表示頂點的個數,E表示邊的個數,排序E個邊加上E次UnionFind操作
時間復雜度:O(Elog2E+Elog2V)
Prim
有了推論1,Prim算法的正確性理解起來就很簡單了,一直只對最小生成樹子集進行切割,然后選擇出最小生成樹子集與其他連通分量的最小代價邊就OK了。Prim算法就是一直選擇最小生成樹子集與其他頂點連接的最小代價邊。
Prim算法維持這樣一個最小堆,存儲最小生成樹子集以外的頂點,與最小生成樹子集臨接的頂點的權重是其臨接邊的值,其余的最小堆中的頂點權重都是無窮。Prim算法初始將起始頂點在最小堆中的權重置為0,其余的頂點置為無窮。然后從最小堆中一直取權重最小的頂點,即選擇最小代價邊加入最小生成樹,如果取出的頂點的臨接頂點不在最小生成樹中,且這個臨接頂點在最小堆中的權重比邊大,則更新臨接頂點在最小堆的權重,直到從最小堆中取出所有的頂點,就得到了一顆最小生成樹。
偽代碼:
PRIM(g,s)
let heap be new MinHeap
let result be new Array
for i from 1 to the number of vertex in g
let vertex be new Vertex(i)
vertex.weight = INT_MAX
heap.insert(vertex)
end
heap.decrease(s,0)
while heap.empty() == false
vertex v = heap.top()
for u equal to every vertex adjacent to v
if heap.isNotInHeap(u) and v->u < heap.getWeightOfNode(u)
result[u] = v
heap.decrease(u,v->u)
end
end
return result
V表示頂點的個數,E表示邊的個數,對V個頂點和E條邊進行decrease操作
時間復雜度:O(Elog2V+Vlog2V)
Boruvka
Kruskal是根據所有邊中最小代價邊的一端的連通分量分割,Prim根據最小生成子樹的子集分割,Boruvka根據所有的連通分量分割,實際上都是基于推論1。Boruvka算法將所有連通分量與其他連通分量的最小代價邊選擇出來,然后將這些邊中未加入最小生成樹子集的加進去,一直到生成最小生成樹。
Boruvka算法同樣使用了UnionFind去記錄連通分量,用cheapest數組記錄連通分量與其他連通分量連接的最小代價邊的編號。
偽代碼:
Boruvka(g)
let uf be new UnionFind
let cheapest be new Array
let edges be all the edge of g
let numTree = the number of vertex in g
let result be new Array
for i from 1 to number of vertex in g
cheapest[i] = -1
end
while numTree > 0
for i from 1 to the number of edge in g
let set1 = uf.find(edges[i].src)
let set2 = uf.find(edges[i].des)
if set1 == set2
continue
if cheapest[se1] == -1 or edges[cheapest[set1]].weight > edges[i].weight
cheapest[set1] = i
if cheapest[set2] == -1 or edges[cheapest[set2]].weight > edges[i].weight
cheapest[set2] = i
end
for i from 1 to the number of vertex in g
if cheapest[i] != -1
let set1 = uf.find(edges[cheapest[i]].src)
let set2 = uf.find(edges[cheapest[i]].des)
if set1 == set2
continue
result[edges[cheapest[i]].src] = edges[cheapest[i]].des
uf.union(set1,set2)
numTree = numTree - 1
end
end
return result
時間復雜度:O(Elog2V),V表示頂點的個數,E表示邊的個數
單源最短路徑(Single-Source-Shortest-Paths)
給出一張連通、有向圖,找出一個頂點s到其他所有頂點的最短路徑。可以看到,如果圖中存在負環,不存在最短路徑。因為存在負環就可以無限循環負環得到更短的路徑。
看通用的算法之前,同樣要討論一下問題的性質。
假設,存在一條頂點s到頂點v的最短路徑,i、j為路徑上的兩個頂點。那么在這條s到v最短路徑上,i到j的路徑是否是i到j的最短路徑?是的,如果存在i到j的更短路徑,就等價于存在一條s到v的更短路徑,這與假設不符。也就是說,如果存在一條從s到v的最短路徑,這條路徑上任意兩個頂點的路徑都是這兩個頂點的最短路徑。那么,這個問題就具有動態規劃的狀態轉移特征。
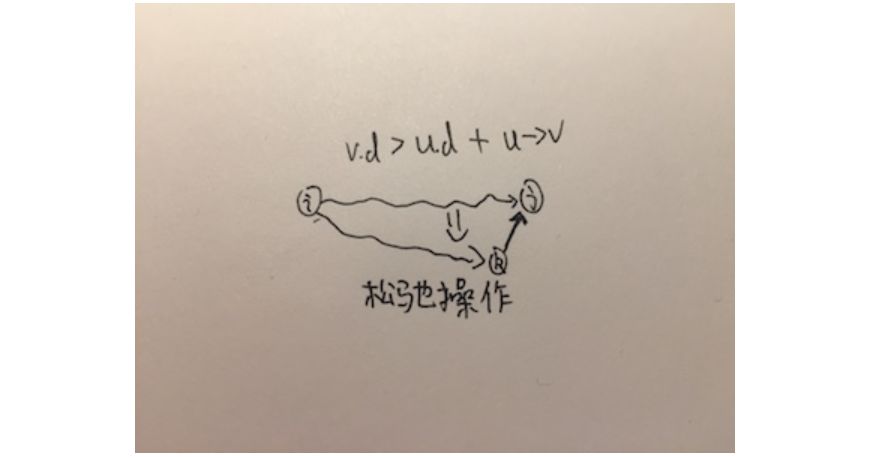
解決此問題的樸素想法就是求出所有頂點s到頂點v的路徑,然后取最小值。那么要是實現這個步驟,就要為v點存儲一個估計值d,并設起始為無窮,如果有到達v的路徑小于這個估計值,更新這個估計值,并且記錄v的現階段最小路徑。這步操作叫做松弛操作(relax)。假設u為小于估計值路徑上的上個頂點。
RELAX(u,v,result)
if v.d > u.d + u->v
v.d = u.d + u->v
result[v] = u
那么,算法要做的就是一直松弛到達v頂點的路徑,從無窮直到最小路徑。可以看到,所有的求最短路徑的算法都要基于這個操作去求解,不同的算法只能就是執行這個操作順序不同或者次數不同。那么松弛操作會不會出問題,會不會松弛操作做過頭了,將v的估計值松弛的比最短路徑還小?不會,在算法運行期間,對于所有頂點,一直對頂點進行松弛操作,頂點的預估值不會低于最短路徑。以下用結構證明法證明。
假設:u代表任意一個連接v的頂點,s->v代表s到v的邊,s~>v代表s到v的最短路徑。
命題:對到達v的所有路徑松弛操作有v.d >= s~>v
證明:
對于v=s的情況,v.d=0 s~v即s~s也為0,命題得證
假設對于頂點u,u.d >= s~>u成立。
有s~>v <= s~>u + u->v,因為s~>v是一條最短路徑,對于任意一條經過u到達v的路徑,必小于最短路徑。
s~>v <= u.d + u->v
因為經過松弛操作v.d = u.d + u->v,所以v.d >= s~>v,命題得證。
松弛操作只能同時對一條邊起作用。所以,最短路徑長為n的路徑,只能從最短路徑長為n-1的路徑,轉移過來。這里就得到了這個問題最重要的性質,單源最短路徑問題是個最短路徑每次遞增一的動態規劃問題。
單源最短路徑性質:此問題是個最短路徑每次長度遞增一的動態規劃問題。
在介紹通用算法之前,先介紹一種專對于有向無環圖很巧的算法。
有向無環圖單源最短路徑(DAG-Shortest-Paths)
對于有向無環圖,可以先對圖進行拓撲排序,然后按拓撲排序的順序對每個頂點作為出度的邊進行松弛操作,就得到了問題的一個解。以下證明算法的正確性。
假設v為對圖拓撲排序后的某個頂點。當對v作為出度的邊進行松弛操作前,所有能到達v的路徑都已經做過了松弛操作,此時已經找到了到達v的最短路徑。那么,當對所有頂點作為出度的邊進行松弛操作后,所有頂點的最短路徑就已經被找到。算法的正確性得到證明。
偽代碼:
DAG-SHORTEST-PATHS(g)
let sorted = TOPOLOGICAL-SORTING-GREEDY(g)
let result be new Array
for u equal to every vertex in sorted
for v equal to every vertex adjacent to u
if v.d > u.d + u->v
RELAX(u,v,result)
end
end
return result
時間復雜度:Θ(V+E),V表示頂點的個數,E表示邊的個數
接下來介紹兩種通用的算法Bellman-Ford和Dijkstra。Bellman-Ford和Dijkstra有什么聯系呢?Bellman-Ford可以解決有負權重圖的單源最短路徑問題,并且可以偵測出圖中是否存在負環。Dijkstra只能解決沒有負權重邊的圖的單源最短路徑問題。Bellman-Ford是進行必須的最少次數的松弛操作。而Dijkstra發現,只要沒有負權重邊,還能進行更少的松弛操作解決問題。
Bellman-Ford
Bellman-Ford是最通用的解決單源最短路徑算法,初始將所有頂點估計值設為無窮,將源點設為零。然后,對所有邊進行松弛操作,這個步驟作為內部循環。再將這個步驟做圖的頂點個數減一次。
Bellman-Ford的正確性不難證明,可以看到隨著Bellman-Ford算法內部的循環,Bellman-Ford找到的最短路徑的長度也在增加。首先證明內部循環在循環到第n次時,找到了所有最短路徑長為n的路徑。我們用結構證明法。在以下證明中,可以看出Bellman-Ford雖然不是經典的動態規劃算法,但是其原理是基于這個問題的動態規劃性質的。
證明:
對于n=0時,最短路徑為0,命題得證。
假設所有最短路徑為n-1的路徑已經被找到。因為根據單源最短路徑的動態規劃性質,最短路徑長為n的路徑,可以從最短路徑長為n-1的路徑,轉移過來的。因為Bellman-Ford算法會對所有的邊進行松弛操作。所以,所有長為n的最短路徑會從相應的長為n-1的最短路徑找到。命題得證。
只要最短路徑上不存在負環,那么所有最短路徑就必小于V-1。所以,Bellman-Ford內部循環執行V-1次,能找到最長的最短路徑,也就是能找到所有的最短路徑。Bellman-Ford正確性證畢。
Bellman-Ford實現也很簡單,這里添加一個flag位,提前省去不必要的循環。
偽代碼:
BELLMAN-FORD(g,s)
let edges be all the edge of g
let result be new Array
for i from 1 to the number of vertex of g
result[i] = INT_MAX
end
result[s] = 0
for i from 1 to the number of vertex of g minus 1
let flag = false
for j from 1 to the numnber of edge of g
let edge = edges[j]
if result[edge.src] != INT_MAX and edge.src > edge.des + edge.weight
RELAX(u,v,result)
flag = true
end
if flag == false
break
end
return result
時間復雜度:O(V?E),V表示頂點的個數,E表示邊的個數
為什么Bellman-Ford算法可以偵測出有負環?算法完成后再對圖的所有邊進行一次松弛操作,如果最短路徑求得的值改變了,就是出現了負環。這個證明看一下松弛操作的定義就行了。根據松弛操作的性質,頂點的估計在等于最短路徑后不會再改變了,如果改變了就是出現了負環,從而沒有得到最短路徑。
Dijkstra
Dijkstra是個貪心算法,樸素的想一下,用貪心算法怎么解決問題。既然沒有負權邊,選出當前階段最短的路徑,這個路徑就應該是到達這個路徑終點的最短路徑。
Dijkstra就是這樣一個貪心算法,初始將所有頂點估計值設為無窮,將源點設為零。維護一個集合S代表已經找到的最短路徑頂點,然后從集合S外所有頂點,選擇有最小的估計值的頂點加入到集合中,然后再對這個頂點在S中的臨接頂點做松弛操作,一直到所有頂點都在集合S中。
Dijkstra的貪心選擇使用簡單的反證法就可以證出。
假設,現階段要選從s到某個頂點u的路徑作為最短路徑加入到集合S中,并且這個選擇是錯誤的。有另一條最短路徑從s到達u,那么這條路徑和原選擇的路徑肯定不一致,經過不同的頂點,假設這條最短路徑上到達u的前一個頂點為k,既然這是一條從s到達u的最短路徑,那么從s到k肯定比從s到v小,那么算法會先選擇從s到k,然后選擇最短路徑,不會選擇假設的路徑,這與假設矛盾,假設不成立,貪心選擇正確性得證。
以下是算法導論上的證明,嘗試從實際發生了什么去證明正確性,我認為有點clumsy(笨重),核心的想法其實和上面簡單的反證法一致。
命題:選擇有最小估計值的頂點加入集合S,那么這個估計值必定是這個頂點的最小路徑。
同樣使用反證法來證,并且關注已經選擇了最小預估值的頂點但還沒加入頂點S時的情形。
假如選擇了頂點u,這時,將從s到u作為最小條路徑加入到S中,分為兩種情況。情況一,選擇的從s到u的路徑就是最短路徑,那么命題已經得證。情況二,選擇的從s到u的路徑不是最短路徑,存在u.d>s~>u。這種情況下,可以找到一個頂點x,使得x在集合S中,并在對x進行松弛操作后,找到另一個頂點y,使得y不在集合中且y的估計值就等于s到y的最短路徑即s~>y。x可以與s重合,y可以與u重合。
那么有y.d = s~>y
因為從s到y是從s到u的子路徑,有s~>u >= s~>y
得出s~>u >= y.d
因為選擇了頂點u,有u.d <= y.d
得出s~>u >= u.d
這與假設矛盾,所以假設不成立,命題得證。
實現和時間復雜度與Prim算法類似,集合S用最小堆實現。
偽代碼:
DIJKSTRA(g,s)
let heap be new MinHeap
let result be new Array
for i from 1 to the number of vertex in g
let vertex be new Vertex(i)
vertex.d = INT_MAX
heap.insert(vertex)
end
heap.decrease(s,0)
while heap.empty() == false
vertex u = heap.top()
for v equal to every vertex adjacent to u
if heap.isNotInHeap(v) and u.d v.d > u.d + u->v
RELAX(u,v,result)
heap.decrease(v,v.d)
end
end
return result
V表示頂點的個數,E表示邊的個數,對V個頂點和E條邊進行decrease操作
時間復雜度:O(Elog2V+Vlog2V)
可以看到,如果運氣好,Bellman-Ford不需要V次循環就可以找到所有最短路徑,但是運氣不好,Bellman-Ford要經過最少V次循環,這就是上文說到的,Bellman-Ford是進行必須的最少次數的松弛操作。而如果不存在負權重邊,Dijkstra可以進行更少次的松弛操作,至多對每個頂點連接的邊進行一次松弛操作就可以了,Bellman-Ford與Dijkstra的聯系實際上就是動態規劃與貪心算法的聯系。Bellman-Ford和Dijkstra算法本質都是單源最短路徑性質。
全對最短路徑(All-Pair-Shortest-Paths)
全對最短路徑就是將圖中任意兩點之間的最短路徑求出來,輸出一個矩陣,每個元素代表橫坐標作為標號的頂點到縱坐標作為標號的頂點的最短路徑。當然,可以對所有頂點運行一次Bellman-Ford算法得出結果,不過這樣的復雜度就太高了。嘗試去找到更好的算法解決這個問題。
既然單源最短路徑是個最短路徑遞增一的動態規劃問題,嘗試對全對最短路徑使用這種性質,然后看看能不能降低復雜度。
假設有n個頂點,dpij代表從頂點i到頂點j的最短路徑,假設這條最短路徑長為m,且k為任意頂點。那么,根據這個問題的動態規劃狀態轉移特征,dpij是由長度為m?1的dpik加上k->j轉移過來的。
看來即使在單源最短路徑動態規劃的性質上進行求解,復雜度仍然很高。
嘗試不從最短路徑長度角度考慮動態規劃,從頂點角度去考慮動態規劃,引出一個通用的算法Floyd-Warshall。
Floyd-Warshall
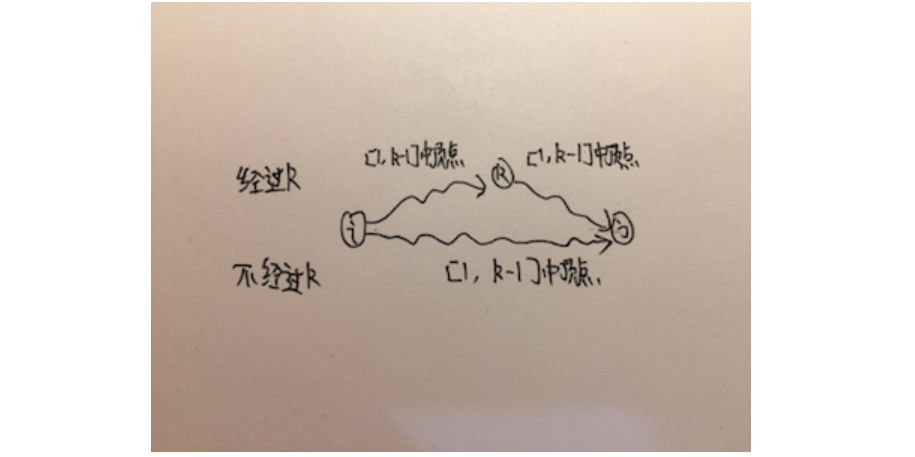
好,從頂點的角度去思考動態規劃。從頂點i到頂點j要經過其他頂點,假設經過的頂點為k。然后根據解動態規劃的經驗,猜想dpij與dpik和dpkj怎么能沾到邊?假設從i到j只需要經過[1,k]集合中的頂點。如果從i到j經過k,那么dpik就代表從i到k的最短路徑,dpkj就代表從k到j的最短路徑,dpij就等于從dpik和dpkj轉移過去,而dpik和dpkj都不經過k,都只需要經過[1,k-1]集合中的頂點。如果從i到j不經過k,dpij就等于從i到j只需要經過[i,k-1]集合中的頂點時的dpij。
偽代碼:
FLYOD-WARSHALL(g)
let dp be new Table
for i from 1 to the number of vertex in g
for j from 1 to the number of vertex in g
dp[i][j] = g[i][j]
end
end
for k from 1 to the number of vertex in g
for i from 1 to the number of vertex in g
for j from 1 to the number of vertex in g
if dp[i][k] + dp[k][j] < dp[i][j]
dp[i][j] = dp[i][k] + dp[k][j]
end
end
end
return dp
時間復雜度:Θ(V3),$V$表示頂點的個數
Johnson
對于稀疏圖的話,還有辦法降低算法復雜度。直觀上看,對于稀疏圖,對每個頂點運行Dijkstra算法是快過Floyd-Warshall算法的,但是這樣要求圖中不能有負權邊。那么,可不可以將有負權邊的圖轉化為沒有負權邊的圖。Johnson就是這樣一個算法,將所有的邊進行重新賦權重(reweight),然后再對所有頂點運行Dijkstra算法。那怎么進行重新賦權重呢?樸素想法是找出所有的邊中最小的值,然后所有邊增加這個值。很可惜,這樣不行。考慮這樣一個情況,頂點a到b的最短路徑有3條邊,最短路徑為4。有a到b另一條路徑只經過一條邊,路徑權重為5。如果對所有邊增加1權重,那么頂點a到頂點b的最短路徑就改變了。重新賦權重改變了最短路徑是明顯有問題的。
可以看出重新賦權重有兩點要求:
1.對起點和終點相同的路徑改變同樣的權重,保持原來的最短路徑結果。
2.所有邊重新賦權以后不存在負權邊。
Johnson算法先對頂點重新賦值,然后將邊的重新賦值由兩端頂點的重新賦的值得出。假設u和v為相鄰的兩個頂點。
這樣定義w’()函數以后,對路徑重新賦的值影響的只有起點和終點兩個頂點,中間頂點重賦的值都被消掉了。等價于保持原來的最短路徑結果。那么,怎么保證第二點?Johnson算法會為圖增加一個頂點s,然后對圖運行一次Bellman-Ford算法。得出新增的頂點s與所有原頂點的最短路徑,這個最短路徑就是h()數的值。
而且在運行Bellman-Ford算法的時候,正好可以偵測出圖中是否有負環。
偽代碼:
JOHNSON(g)
let s be new Vertex
g.insert(s)
if BELLMAN-FORD(g,s) == flase
there is a negative cycle in graph
else
for v equal to every vertex in g
h(v) = min(v~>s)
end
for (u,v) equal to every edge in graph
w’(u,v) = w(u,v) + h(u) - h(v)
end
let result be new Table
for u equal to every vertex in g
DIJSKTRA(g,u)
for v equal to every vertex in g
result[u][v] = min(u~>v) + h(v) - h(u)
end
end
return result
時間復雜度:O(V?Elog2V+V2log2V+V?E),V表示頂點的個數,E表示邊的個數
證明了這么多的算法正確性,可以看到,證明是有技巧的,常用的只有三個方法,反證法、結構歸納法、Cut-And-Paste法。
經過圖論的探討,便可以理解算法與數學之間緊密的聯系。解決問題要對問題本身的特征、屬性進行總結或者提煉。有時要對問題進行相應的轉化。然后根據問題的特征、性質推導出定理。再將定理拓展,提出推論
-
圖論
+關注
關注
0文章
6瀏覽量
7218 -
DFS
+關注
關注
0文章
26瀏覽量
9181
原文標題:圖論的各種基本算法
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數據結構】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
鎵的化學性質與應用
變頻器負載性質了解嗎?如何維護變頻器?
【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+內容簡介
【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+介紹基礎硬件算法模塊
傅里葉變換的基本性質和定理
導磁材料的主要性質有哪些
平衡電橋的性質與特點是什么
渦流損耗的大小與鐵芯材料的性質
差示掃描量熱儀:揭示材料熱性質的秘密武器

綜合熱分析儀:探索物質熱性質的重要工具

變壓器空載電流的性質和作用是什么
RLC串聯電路的性質如何判斷
靜電平衡狀態下帶電導體的性質是什么
差示掃描量熱儀:探索物質熱性質的強大工具





 圖論的基本算法及性質
圖論的基本算法及性質










評論