1. 歸并排序(遞歸版)
歸并排序(MERGE-SORT)是利用歸并的思想實現的排序方法,該算法采用經典的分治策略,即分為兩步:分與治。
- 分:先遞歸分解數組成子數組
- 治:將分階段得到的子數組按順序合并
我們來具體看看例子,假設我們現在給定一個數組:[6,3,2,7,1,3,5,4],我們需要使用歸并算法對其排序,其大致過程如下圖所示:
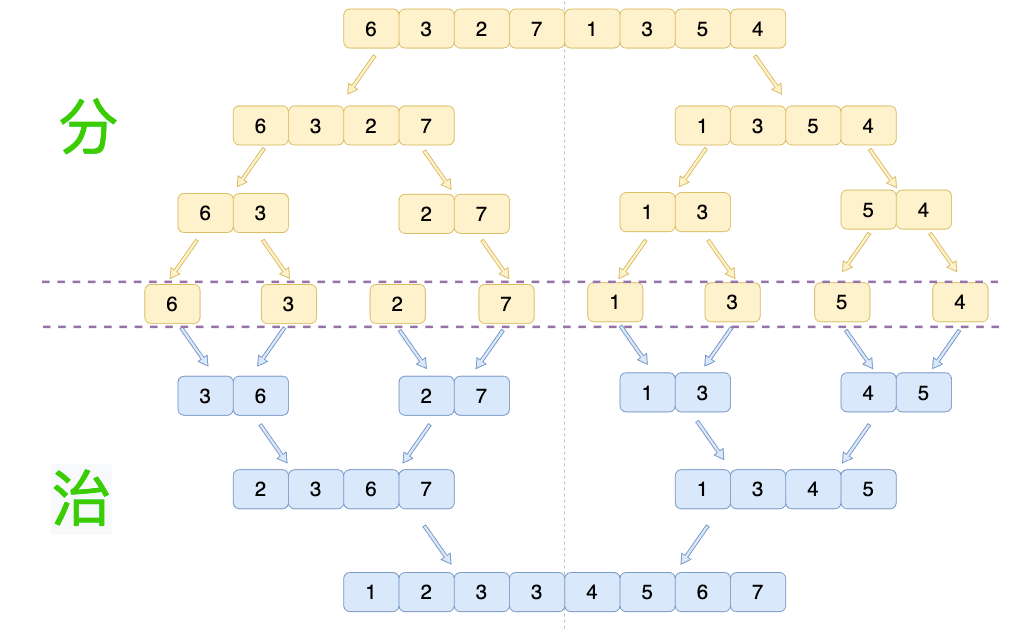
分階段可以理解為就是遞歸拆分子序列的過程,遞歸的深度為log2n。而治的階段則是將兩個子序列進行排序的過程,我們通過圖解看看治階段最后一步中是如何將[2,3,6,7]和[1,3,4,5]這兩個數組合并的。

圖中左邊是復制的臨時數組,而右邊是原數組,我們將左右指針對應的值進行大小比較,將較小的那個數放入原數組中,然后將相應的指針右移。比如第一步中,我們比較左邊指針L指向的4和右指針R指向的1,R指向的1小,則把1放入原數組中的第一個位置中,然后R指針向右移動。后面再繼續,直到左邊臨時數組的元素都按序覆蓋了右邊的原數組。最后我們通過上圖再結合源碼來看看吧:
class Solution {
public int[] sortArray(int[] nums) {
sort(0, nums.length - 1, nums);
return nums;
}
// 分:遞歸二分
private void sort(int l, int r, int[] nums) {
if (l >= r) return;
int mid = (l + r) / 2;
sort(l, mid, nums);
sort(mid + 1, r, nums);
merge(l, mid, r, nums);
}
// 治:將nums[l...mid]和nums[mid+1...r]兩部分進行歸并
private void merge(int l, int mid, int r, int[] nums) {
int[] aux = Arrays.copyOfRange(nums, l, r + 1);
int lp =l, rp = mid + 1;
for (int i = lp; i <= r; i ++) {
if (lp > mid) { // 如果左半部分元素已經全部處理完畢
nums[i] = aux[rp - l];
rp ++;
} else if (rp > r) { // 如果右半部分元素已經全部處理完畢
nums[i] = aux[lp - l];
lp ++;
} else if (aux[lp-l] > aux[rp - l]) { // 左半部分所指元素 > 右半部分所指元素
nums[i] = aux[rp - l];
rp ++;
} else { // 左半部分所指元素 <= 右半部分所指元素
nums[i] = aux[lp - l];
lp ++;
}
}
}
}
我們可以看到,分階段的時間復雜度是logN,而合并階段的時間復雜度是N,所以歸并算法的時間復雜度是O(N*logN),因為每次合并都需要對應范圍內的數組,所以其空間復雜度是O(N);
2. 歸并排序(迭代版)
上面的歸并排序是通過遞歸二分的方法進行數組切分的,其實我們也可以通過迭代的方法來完成這步,看下圖:

其因為數組,所以我們直接通過迭代從1開始合并,其中sz就是合并的長度,這種方法也可以稱為自底向上的歸并,其具體的代碼如下
class Solution {
public int[] sortArray(int[] nums) {
int n = nums.length;
// sz= 1,2,4,8 ... 排序
for (int sz = 1; sz < n; sz *= 2) {
// 對 arr[i...i+sz-1] 和 arr[i+sz...i+2*sz-1] 進行歸并
for (int i = 0; i < n - sz; i += 2*sz ) {
merge(i, i + sz - 1, Math.min(i+sz+sz-1, n-1), nums);
}
}
return nums;
}
// 和遞歸版一樣
private void merge(int l, int mid, int r, int[] nums) {
int[] aux = Arrays.copyOfRange(nums, l, r + 1);
int lp =l, rp = mid + 1;
for (int i = lp; i <= r; i ++) {
if (lp > mid) {
nums[i] = aux[rp - l];
rp ++;
} else if (rp > r) {
nums[i] = aux[lp - l];
lp ++;
} else if (aux[lp-l] > aux[rp - l]) {
nums[i] = aux[rp - l];
rp ++;
} else {
nums[i] = aux[lp - l];
lp ++;
}
}
}
}
3. 總結
好了,歸并算法就介紹完了,再來總結一下:
歸并排序是一種十分高效的排序算法,其時間復雜度為O(N*logN)。歸并排序的最好,最壞的平均時間復雜度均為O(nlogn),排序后相等的元素的順序不會改變,所以也是一種穩定的排序算法。歸并排序被應用在許多地方,其java中Arrays.sort()采用了一種名為TimSort的排序算法,其就是歸并排序的優化版本。
-
JAVA
+關注
關注
19文章
2971瀏覽量
104848 -
代碼
+關注
關注
30文章
4798瀏覽量
68728 -
排序算法
+關注
關注
0文章
53瀏覽量
10085 -
數組
+關注
關注
1文章
417瀏覽量
25975
發布評論請先 登錄
相關推薦
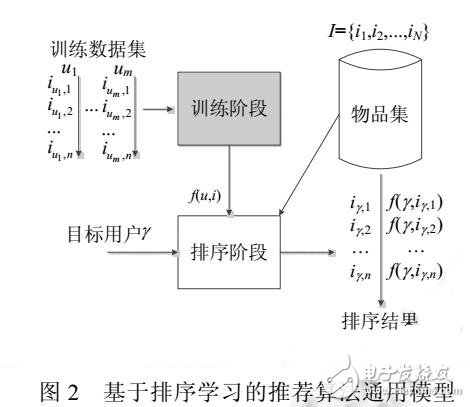
基于排序學習的推薦算法




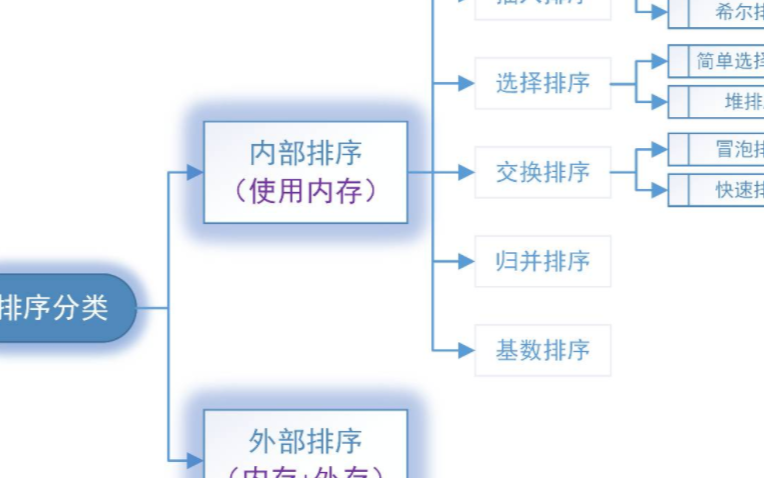
 排序算法有哪些
排序算法有哪些












評論