寫在前面 Ⅰ

前面寫了關于ADC采集電壓的文章，大家除了求平均的方式來處理采樣值，還有沒有使用到其他的方式來處理采集值呢？

在某些情況下就需要對一組數(shù)據(jù)進行排序，并提取頭特定的數(shù)據(jù)出來使用。

排序的應用場合很多，我這里就不再一一舉例說明，掌握排序的基本算法，到時候遇到就有用武之地。

排序算法分類 Ⅱ

1.按存儲分類：內(nèi)部排序和外部排序

內(nèi)部排序：是數(shù)據(jù)記錄在內(nèi)存中進行排序；

外部排序：是因排序的數(shù)據(jù)很大，一般一次不能容納全部的排序記錄，在排序過程中需要訪問外存。

內(nèi)部排序高速、有效，是我們比較常用的排序方法。外部排序速度慢，效率低，一般不建議使用外部排序，比較實用的排序還是只有內(nèi)部排序。

2.內(nèi)部排序分類：插入排序、選擇排序、交換排序、歸并排序、基數(shù)排序。

排序的分類大致為如下圖：

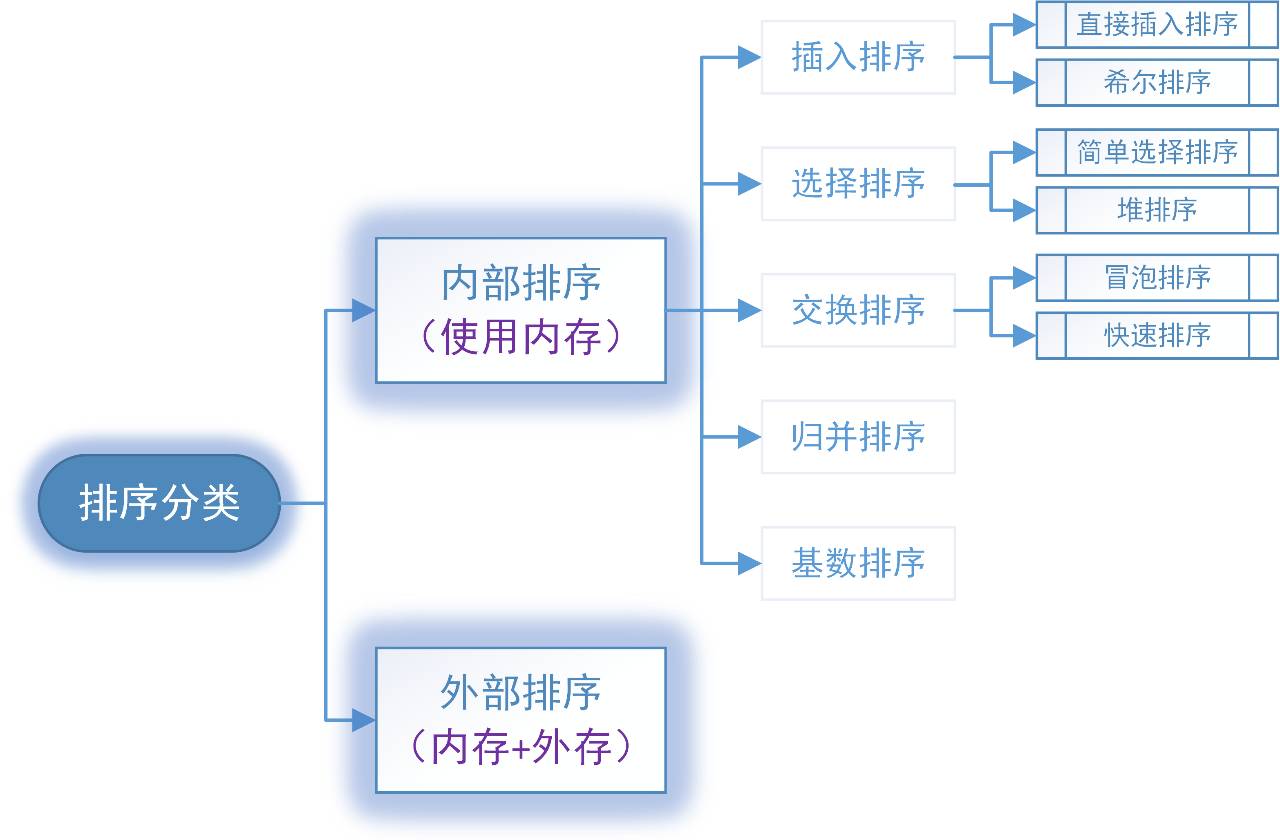
在內(nèi)部排序中，最常見、有效且實用的排序算是交換排序，本文將在下面章節(jié)重點講述交換排序中的冒泡排序和快速排序。

交換排序 Ⅲ

1.冒泡排序

冒牌排序是我們讀書時最先接觸的一種排序算法，也是比較經(jīng)典的排序算法。

冒泡排序就是在要排序的一組數(shù)中，對當前還未排好序范圍內(nèi)的全部數(shù)，自上而下對相鄰的兩個數(shù)依次進行比較和調(diào)整，讓較大的數(shù)往下沉，較小的往上冒。即：每當兩相鄰的數(shù)比較后發(fā)現(xiàn)它們的排序與排序要求相反時，就將它們互換。

原始的冒泡排序函數(shù)：

void bubbleSort(int a[], int n)

{

for(int i =0 ; i< n-1; ++i)

{

for(int j = 0; j < n-i-1; ++j)

{

if(a[j] > a[j+1])

{

int tmp = a[j];

a[j] = a[j+1];

a[j+1] = tmp;

}

}

}

}

其實，原始的冒泡排序不是最后的算法，如果進行某一趟排序時并沒有進行數(shù)據(jù)交換，則說明數(shù)據(jù)已經(jīng)按要求排列好，可立即結(jié)束排序，避免不必要的比較過程。

對冒泡排序常見的改進方法是加入標志性變量，用于標志某一趟排序過程中是否有數(shù)據(jù)交換。

第1種改進法：設置一標志性變量pos,用于記錄每趟排序中最后一次進行交換的位置。由于pos位置之后的記錄均已交換到位,故在進行下一趟排序時只要掃描到pos位置即可。

void Bubble_1( int r[], int n)

{

int pos = 0;

int i;

int j;

int tmp;

i = n - 1;

while(i > 0)

{

for(j=0; j

{

if(r[j] > r[j+1])

{

pos = j; //記錄交換的位置

tmp = r[j];

r[j] = r[j+1];

r[j+1] = tmp;

}

}

i= pos;

}

}

第2種改進法：傳統(tǒng)冒泡排序中每一趟排序操作只能找到一個最大值或最小值,我們考慮利用在每趟排序中進行正向和反向兩遍冒泡的方法一次可以得到兩個最終值(最大者和最小者) , 從而使排序趟數(shù)幾乎減少了一半。

void Bubble_2(int r[], int n)

{

int low = 0;

int high= n -1;

int tmp,j;

while(low < high)

{

for(j=low; j//正向冒泡,找到最大者

{

if(r[j]> r[j+1])

{

tmp = r[j];

r[j]=r[j+1];

r[j+1]=tmp;

}

--high;

for(j=high; j>low; --j)//反向冒泡,找到最小者

{

if(r[j]

{

tmp = r[j];

r[j]=r[j-1];

r[j-1]=tmp;

}

++low;

}

}

}

}

2.快速排序

大致步驟如下：

1）選擇一個基準元素,通常選擇第一個元素或者最后一個元素。

2）通過一趟排序?qū)⒋判虻挠涗浄指畛瑟毩⒌膬刹糠郑渲幸徊糠钟涗浀脑刂稻然鶞试刂敌　Ａ硪徊糠钟涗浀脑刂当然鶞手荡蟆?/p>

3）此時基準元素在其排好序后的正確位置。

4）然后分別對這兩部分記錄用同樣的方法繼續(xù)進行排序，直到整個序列有序。

舉例：

對無序數(shù)組[6 2 4 1 5 9]排序：

a),先把第一項[6]取出來,

用[6]依次與其余項進行比較:

如果比[6]小就放[6]前邊,2 4 1 5都比[6]小,所以全部放到[6]前邊；

如果比[6]大就放[6]后邊,9比[6]大,放到[6]后邊；

一趟排完后變成下邊這樣:

排序前62 4 1 5 9

排序后 2 4 1 569

b),對前半邊[2 4 1 5]繼續(xù)進行快速排序

重復步驟a)后變成下邊這樣:

排序前24 1 5

排序后 124 5

前半邊排序完成,總的排序也完成:

排序前:[6 2 4 1 5 9]

排序后:[1 2 4 5 6 9]

排序結(jié)束

代碼

將前后分開函數(shù)：

int partition(int unsorted[], int low, int high)

{

int pivot = unsorted[low];

while(low < high)

{

while((low < high) && (unsorted[high] >= pivot))

--high;

unsorted[low] = unsorted[high];

while((low < high) && (unsorted[low] <= pivot))

++low;

unsorted[high] = unsorted[low];

}

unsorted[low] = pivot;

return low;

}

快速排序函數(shù)：

void quickSort(int unsorted[], int low, int high)

{

int loc = 0;

if(low < high)

{

loc = partition(unsorted, low, high);

quickSort(unsorted, low, loc -1);

quickSort(unsorted, loc + 1, high);

}

}

舉例測試：

void Main(void)

{

int i;

int a[6] = {6, 2, 4, 1, 5, 9};

quickSort(a, 0, 5);

for(i=0; i<6; i++)

printf("a[%d] = a[%d]\n", i, a[i]);

}

在排序算法中，這兩種是較重要的排序算法，其他算法在特定場合也有用武之地，本文暫時講述到這里。