01 前言
雙目相機標定,從廣義上講,其實它包含兩個部分內(nèi)容:
兩臺相機各自誤差的標定(單目標定)
兩臺相機之間相互位置的標定(狹義,雙目標定)
在這里我們所說的雙目標定是狹義的,講解理論的時候僅指兩臺相機之間相互位置的標定,在代碼實踐的時候,我們才說完整的雙目標定。 首先來思考一個問題:為什么要進行雙目標定?
這是因為在許多三維重建算法中,我們都要知道兩臺相機之間的相對位置關系,這樣才能進行距離計算。
雙目標定前后,雙目模型對比如下圖所示: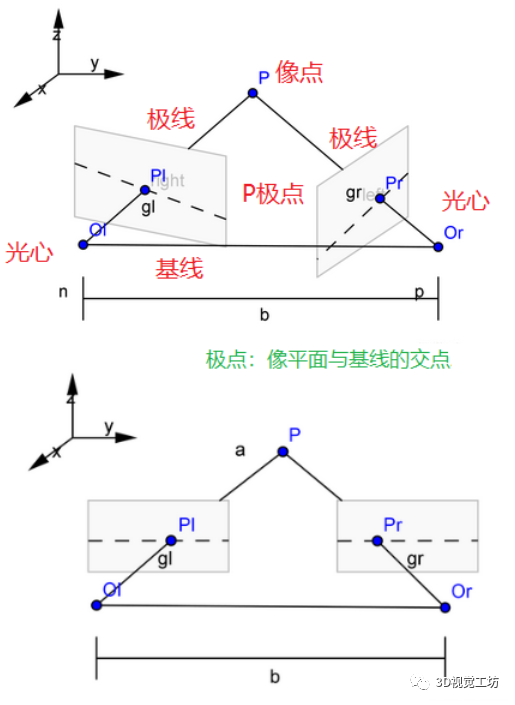
圖1 標定模型 [1] 其中:
基線:兩個光心的連線稱為基線;
極平面:物點(空間點M)與兩個光心的連線構成的平面稱為極平面;
極線:極平面與成像平面的交線
極點:極線的一端,基線與像平面的交點
像點:極線的一端,光心與物點連線與像平面的交點;
可以看出:
校正前,相機的光心不是相互平行的
校正后,極點在無窮遠處,兩個相機的光軸平行,像點在左右圖像上的高度一致
標定+校正后圖片:
圖1 立體校正后左右相機圖像發(fā)生一定扭曲 [2] 這樣的好處是:比如后續(xù)的立體匹配時,只需在同一行上搜索左右像平面的匹配點即可,能使效率大大提高。
注:可以看出來,最重要的,我們要知道右相機相對于左相機的位姿關系,那我們才可以做校正!
02 單目理論回顧
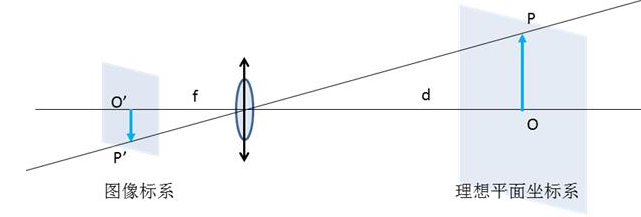
先來回顧下單目標定理論,理想的單目相機模型可以簡化為(圖片來自于[1]):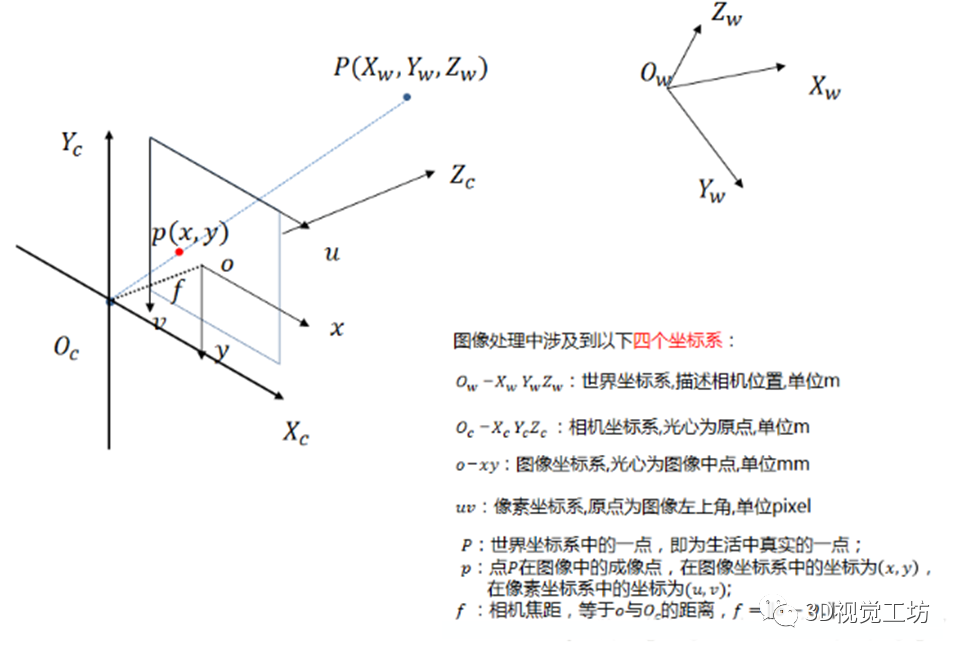
而四大坐標系,包括世界坐標系、相機坐標系、圖像坐標系、像素坐標系,它們之間的轉(zhuǎn)換關系如下: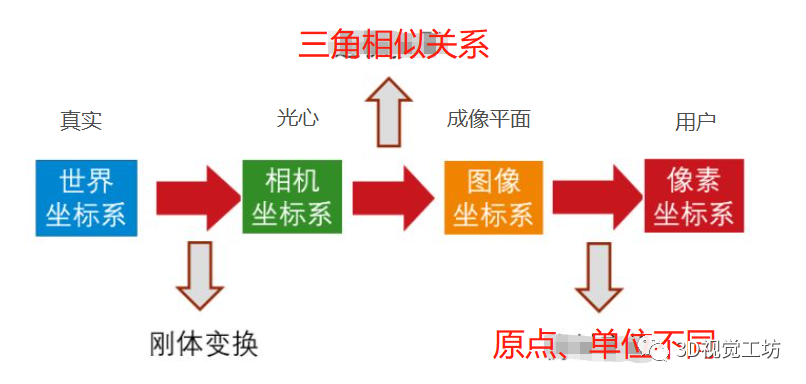
最終,從理想的相機模型,從世界坐標系到像素坐標系的轉(zhuǎn)換關系:
但由于制造原因,使得成像過程(從相機坐標系到圖像坐標系轉(zhuǎn)換過程中)存在著畸變,主要有兩類,徑向畸變和切向畸變,它們可以通過以下公式進行修正:

03 雙目標定公式推導
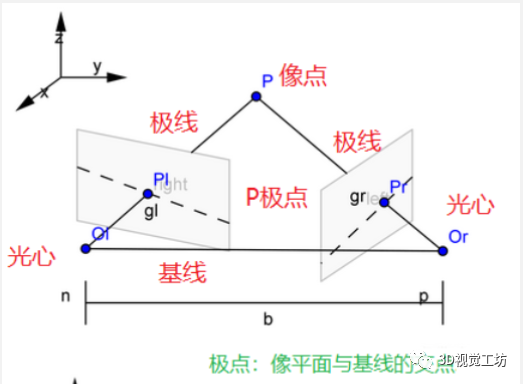
圖3 標定模型 [2] 記:

另外,右相機主點相對于左相機主點,顯然還有: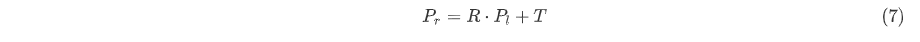

代入上式,因為拍攝了多張圖片,利用最小二乘法,也可以是奇異值分解(數(shù)學的部分比較復雜,在這里忽略),總而言之,最小化誤差,即可得到我們最佳估計的 矩陣,有了這兩個矩陣,我們做個旋轉(zhuǎn)、平移就可以了。 注:雖然得到了旋轉(zhuǎn)、平移矩陣,也但是極線校正的方法有很多,這個我們之后講。
04 極線校正理論推導
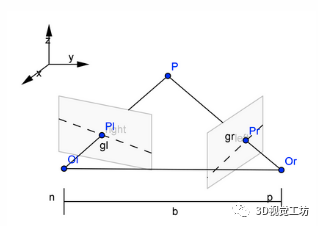
雙目標定后,我們得到了右相機相對于左相機的位姿關系,也就是R、T矩陣,下面一步即做極線校正。校正好處是之后做立體匹配搜索的時候,只需要在同高度附近進行搜索,大幅提升效率。根據(jù)前文的推導,在獲取了R、T矩陣后,我們就要進行極線校正(立體校正),使兩部相機光軸平行,如下所示:
 |
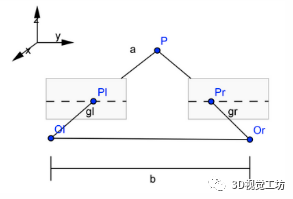 |
| 圖4(a) 立體校正前 [2] | 圖4(b) 立體校正后 [2] |
但是平行的方法有很多,可以:
左相機不動,右相機動。
也可以兩部相機旋轉(zhuǎn)到中間等等。
最常見的校正方法就是Bouguet極線校正方法。
Bouguet極線校正方法:左右相機成像平面各旋轉(zhuǎn)一半,使得左右圖像重投影造成的誤差最小,左右視圖的共同面積最大。
具體步驟(這塊理論推導可以去看論文,這里只給出結論,看不懂沒關系,不妨礙我們使用它):

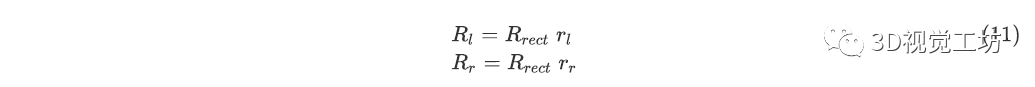
得到這兩個變換矩陣,左、右相機分別乘以這兩個矩陣即可完成變換,其中已經(jīng)包含了平移信息!
再計算重投影矩陣,其實現(xiàn)了像素坐標系(左相機)到世界坐標系之間的轉(zhuǎn)換:

校正后,可以根據(jù)需要對圖像進行裁剪,需重新選擇一個圖像中心,和圖像邊緣從而讓左、右疊加部分最大。
 |
| 圖2 裁剪效果演示 [2] |
審核編輯:劉清
-
3D視覺
+關注
關注
4文章
433瀏覽量
27529
原文標題:一文詳解雙目相機標定理論
文章出處:【微信號:3D視覺工坊,微信公眾號:3D視覺工坊】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
什么是高光譜相機?高光譜相機有什么用?

工業(yè)相機測長儀的組成部分
技術指南丨深視智能3D相機上下對射測厚操作流程

浪潮云洲發(fā)布云洲燭龍雙目結構光3D相機
重磅| 奧比中光全新雙目系列3D相機,搭載自研芯片,為智能機器人而生

奧比中光正式發(fā)布全新Gemini 330系列雙目3D相機

相機標定技術的性能分析與工具比較
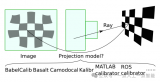
康謀技術 |深入探討:自動駕駛中的相機標定技術





 相機之間為什么要進行雙目標定呢?
相機之間為什么要進行雙目標定呢?













評論