引言
網絡壓縮在AI加速中可以說起到“四兩撥千斤”的作用,網絡參數的減小不僅僅降低了存儲和帶寬,而且使計算邏輯簡單,降低了LUT資源。從本篇開始,我們就一起挖掘一下網絡壓縮算法的類型,原理,實現,以及效果。寫這類算法類文章,一是學習,二是希望能夠令更多做FPGA的人,不再將眼光局限于RTL,仿真,調試,關心一下算法,定會發現FPGA的趣味和神通。
網絡結構
二值化網絡,顧名思義,就是網絡參數只有兩個數值,這兩個數值是+1和-1。在DNN網絡中主要是乘和加法運算,如果參數只有兩個數值,那么乘法的實現就很簡單,僅僅需要符號判斷就可以了。比如輸入數據A,如果和1乘,不變;和-1乘,變為負數。這用LUT很好實現,還節省了DSP的使用。相對于單精度浮點數,存儲減小16倍,帶寬也增加16倍。在計算單元數目相同情況下,比浮點運算速率提高了16倍。當然由于乘法和加法使用LUT數目減少,計算單元也會成倍增長,總的下來計算速率將大幅度提高。
網絡訓練中使用的都是浮點類型參數,這樣做是為了保證訓練的精度。那么這些浮點類型的參數如何量化的只有兩個數值呢?論文中提出了兩種方法,第一種是粗暴型,直接根據權重參數的正負,強行分出1和-1。即:
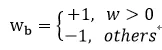
這里wb是二值參數,w是實際權重參數。量化可以看做在原來數據基礎上增加了噪聲,導致數據間最短距離變大。比如原來數據的分辨率為R0,如果增加一個高斯噪聲s,那么其分辨率就增大了。這樣在DNN中矩陣乘法中也引入了噪聲,為:
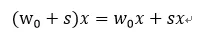
數據分辨率的降低導致了有效信息的損失,但是在大量權重情形下,平均下來可以補償一定的信息損失,即如果有:
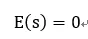
那么在權重無窮多時,有:
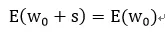
圖1.1 數據增加了噪聲,導致數據分辨率降低
另外一種是隨機型,即以一定概率來選擇1和-1,論文中采用如下公式:

其中“hard sigmoid”函數為:
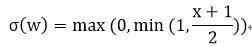
這實際上是對sigmoid函數進行了線性化,這樣做的目的可以減少計算量。因為線性計算只有一個乘法和加法,而sigmoid函數有指數計算。使用隨機量化更能均衡化量化引入的噪聲,消除噪聲造成的信息損失。粗暴型量化可能因為權重參數分布不同而發生較大的“不平衡”,比如負數權重較多,那么導致-1遠遠多于+1,這樣就會出現權重偏移在負方向多一些。如果使用隨機概率模型,即使負數權重多,也會有一定概率出現+1,彌補了+1較少的情況。
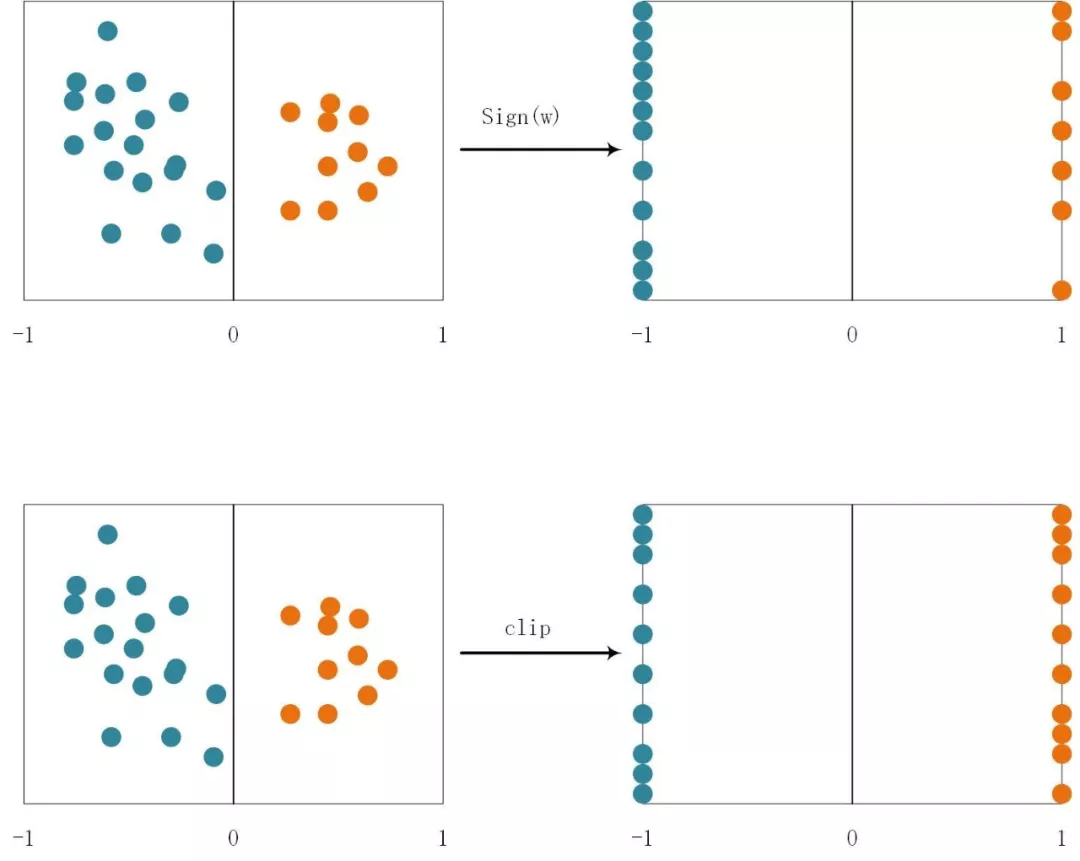
圖1.2 粗暴型和隨機型量化:隨機型量化的分布更加均勻
訓練過程
訓練過程主要包括三個部分:
1) 前向傳播:給定輸入數據,一層一層的計算,前一層激活函數的結果作為下一層的輸入;
2) 反向傳播:計算每一層代價函數的梯度,從最后一層開始計算,反向計算前一層,一直到計算出第一層的梯度值;
3) 更新參數:根據計算出來的梯度和前一時刻的參數,計算出下一時刻的參數。
計算過程可以用圖2.1表示:

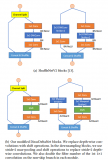
圖2.1 訓練過程

圖2.2 訓練算法
每次量化發生在計算出浮點參數之后,然后在進行前向計算,得到代價函數,進行反向計算代價函數梯度,接著利用前一刻參數計算出下一刻數據,不斷迭代直到收斂。
結果
論文在三個數據集上進行了測試:MNIST,CIFAR-10,SVHN。
MNIST有6萬張內容為0-9數字的訓練圖片,以及1萬張用于測試的28x28大小的灰度圖片。論文研究了兩種量化方式下訓練時間,以及測試出錯率。從中看出隨機量化出錯率更低,更適合用于二值量化。

圖3.1 不同量化方式下的訓練時間以及測試錯誤率:點線表示訓練誤差,連續線表示測試錯誤率
CIFAR-10圖片內容比MNIST復雜一些,包含了各種動物。有5萬張訓練圖片和1萬張32x32大小的測試圖片。
SVHN也是0-9數字圖片,含有604K張訓練圖片和26K的32x32大小的測試圖片。以上三種數據集下使用二值網絡的結果如下圖:
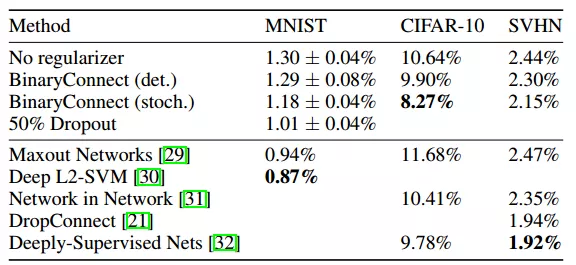
圖3.2 三種數據集結果(錯誤率)比較
從中看出二值網絡錯誤率幾乎和其他網絡模型差不多,但是其大大壓縮了網絡模型。
結論
二值化網絡中參數只用兩個數值表示,實際上僅僅考慮了權重的符號作用。在三種小型簡單的數據集上表現良好。
文獻
1 Matthieu Courbariaux, Y.B., Binary Connect Training Deep Neural Networks with binary weights during propagations. ArXiv preprint, 2016.
編輯:hfy
-
FPGA
+關注
關注
1630文章
21796瀏覽量
605237 -
算法
+關注
關注
23文章
4629瀏覽量
93194
發布評論請先 登錄
相關推薦
EE-257:面向Blackfin處理器的引導壓縮/解壓縮算法

【「從算法到電路—數字芯片算法的電路實現」閱讀體驗】+一本介紹基礎硬件算法模塊實現的好書
【BearPi-Pico H3863星閃開發板體驗連載】LZO壓縮算法移植
Huffman壓縮算法概述和詳細流程
精準捕捉拉曼信號——時間門控拉曼光譜系統實驗結果深度解析
卷積神經網絡的壓縮方法
神經網絡反向傳播算法的原理、數學推導及實現步驟
神經網絡反向傳播算法原理是什么
【RTC程序設計:實時音視頻權威指南】音視頻的編解碼壓縮技術
基于FPGA的網絡加速設計實現




 一文解析網絡壓縮算法的原理實現及結果
一文解析網絡壓縮算法的原理實現及結果











評論