神經網絡反向傳播算法(Backpropagation Algorithm)是一種用于訓練多層神經網絡的算法,其基本原理是通過梯度下降法來最小化損失函數,從而找到網絡的最優權重和偏置。本文將介紹反向傳播算法的原理、數學推導、實現步驟以及在深度學習中的應用。
- 神經網絡概述
神經網絡是一種受人腦啟發的計算模型,由大量的神經元(或稱為節點)組成,每個神經元與其他神經元通過權重連接。神經網絡可以分為輸入層、隱藏層和輸出層。輸入層接收外部輸入數據,隱藏層對輸入數據進行非線性變換,輸出層生成最終的預測結果。
- 損失函數
損失函數(Loss Function)是衡量神經網絡預測結果與真實值之間差異的函數,常見的損失函數有均方誤差(Mean Squared Error, MSE)、交叉熵(Cross-Entropy)等。損失函數的選擇取決于具體問題的性質和需求。
- 梯度下降法
梯度下降法是一種優化算法,用于最小化損失函數。其基本思想是沿著損失函數梯度的方向更新網絡參數(權重和偏置),使得損失函數的值逐漸減小,直至達到最小值。
- 反向傳播算法原理
反向傳播算法是一種利用梯度下降法訓練多層神經網絡的算法。其核心思想是將損失函數關于網絡參數的梯度從輸出層反向傳播到輸入層,從而計算出每個參數的梯度值。具體步驟如下:
4.1 前向傳播
首先,將輸入數據通過網絡的前向傳播,計算出每個神經元的激活值。激活值的計算公式為:
a = f(z)
z = w * x + b
其中,a 表示激活值,f 表示激活函數(如 Sigmoid、ReLU 等),z 表示輸入加權和,w 表示權重,x 表示輸入值,b 表示偏置。
4.2 計算損失函數
根據網絡的輸出值和真實值,計算損失函數的值。損失函數的選擇取決于具體問題的性質和需求。
4.3 反向傳播
從輸出層開始,沿著網絡的連接反向傳播,計算每個參數的梯度值。具體步驟如下:
4.3.1 計算輸出層的梯度
對于輸出層的每個神經元,計算損失函數關于該神經元激活值的梯度。以均方誤差損失函數為例,梯度的計算公式為:
dL/da = (a - y) * f'(z)
其中,dL/da 表示損失函數關于激活值的梯度,a 表示激活值,y 表示真實值,f'(z) 表示激活函數的導數。
4.3.2 計算隱藏層的梯度
對于隱藏層的每個神經元,計算損失函數關于該神經元激活值的梯度。梯度的計算公式為:
dL/da = (w^T * dL/dz) * f'(z)
其中,dL/dz 表示損失函數關于輸入加權和的梯度,w^T 表示權重矩陣的轉置。
4.3.3 更新網絡參數
根據計算出的梯度值,使用梯度下降法更新網絡的權重和偏置。更新公式為:
w_new = w_old - learning_rate * dL/dw
b_new = b_old - learning_rate * dL/db
其中,w_new 和 b_new 分別表示更新后的權重和偏置,w_old 和 b_old 分別表示更新前的權重和偏置,learning_rate 表示學習率,dL/dw 和 dL/db 分別表示損失函數關于權重和偏置的梯度。
- 反向傳播算法的數學推導
5.1 鏈式法則
反向傳播算法的數學基礎是鏈式法則(Chain Rule),它允許我們計算復合函數的導數。對于一個復合函數 L = L(a, z),其關于權重 w 的導數可以表示為:
dL/dw = (dL/da) * (da/dz) * (dz/dw)
5.2 激活函數的導數
常見的激活函數及其導數如下:
- Sigmoid 函數:
f(z) = 1 / (1 + exp(-z)),導數為f'(z) = f(z) * (1 - f(z))。 - ReLU 函數:`f(z) = max(0, z)
-
神經網絡
+關注
關注
42文章
4774瀏覽量
100890 -
神經元
+關注
關注
1文章
363瀏覽量
18470 -
計算模型
+關注
關注
0文章
29瀏覽量
9867 -
數學推導
+關注
關注
0文章
2瀏覽量
5679
發布評論請先 登錄
相關推薦
BP(BackPropagation)反向傳播神經網絡介紹及公式推導





 神經網絡反向傳播算法的原理、數學推導及實現步驟
神經網絡反向傳播算法的原理、數學推導及實現步驟
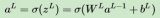










評論