在深度神經(jīng)網(wǎng)絡(luò)（DNN）模型與前向傳播算法中，我們對DNN的模型和前向傳播算法做了總結(jié)，這里我們更進(jìn)一步，對DNN的反向傳播算法（Back Propagation，BP）做一個總結(jié)。

1. DNN反向傳播算法要解決的問題

在了解DNN的反向傳播算法前，我們先要知道DNN反向傳播算法要解決的問題，也就是說，什么時候我們需要這個反向傳播算法？

回到我們監(jiān)督學(xué)習(xí)的一般問題，假設(shè)我們有m個訓(xùn)練樣本：{ ( x1 , y1 ) , ( x2 , y2 ) , ... , ( xm , ym ) }，其中 x 為輸入向量，特征維度為 n_in ，而 y 為輸出向量，特征維度為 n_out 。我們需要利用這 m 個樣本訓(xùn)練出一個模型，當(dāng)有一個新的測試樣本 ( xtest , ? ) 來到時, 我們可以預(yù)測 ytest 向量的輸出。

如果我們采用DNN的模型，即我們使輸入層有 n_in 個神經(jīng)元，而輸出層有 n_out 個神經(jīng)元。再加上一些含有若干神經(jīng)元的隱藏層。此時我們需要找到合適的所有隱藏層和輸出層對應(yīng)的線性系數(shù)矩陣 W ，偏倚向量 b ，讓所有的訓(xùn)練樣本輸入計算出的輸出盡可能的等于或很接近樣本輸出。怎么找到合適的參數(shù)呢？

如果大家對傳統(tǒng)的機器學(xué)習(xí)的算法優(yōu)化過程熟悉的話，這里就很容易聯(lián)想到我們可以用一個合適的損失函數(shù)來度量訓(xùn)練樣本的輸出損失，接著對這個損失函數(shù)進(jìn)行優(yōu)化求最小化的極值，對應(yīng)的一系列線性系數(shù)矩陣W,偏倚向量b即為我們的最終結(jié)果。在DNN中，損失函數(shù)優(yōu)化極值求解的過程最常見的一般是通過梯度下降法來一步步迭代完成的，當(dāng)然也可以是其他的迭代方法比如牛頓法與擬牛頓法。如果大家對梯度下降法不熟悉，建議先閱讀我之前寫的梯度下降（Gradient Descent）小結(jié)。

對DNN的損失函數(shù)用梯度下降法進(jìn)行迭代優(yōu)化求極小值的過程即為我們的反向傳播算法。

2. DNN反向傳播算法的基本思路

在進(jìn)行DNN反向傳播算法前，我們需要選擇一個損失函數(shù)，來度量訓(xùn)練樣本計算出的輸出和真實的訓(xùn)練樣本輸出之間的損失。你也許會問：訓(xùn)練樣本計算出的輸出是怎么得來的？這 個輸出是隨機選擇一系列 W ，b，用我們上一節(jié)的前向傳播算法計算出來的。即通過一系列的計算：

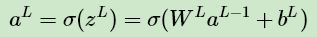
計算到輸出層第L層對應(yīng)的 aL 即為前向傳播算法計算出來的輸出。

回到損失函數(shù)，DNN可選擇的損失函數(shù)有不少，為了專注算法，這里我們使用最常見的均方差來度量損失。即對于每個樣本，我們期望最小化下式：

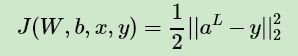
其中，aL 和 y 為特征維度為 n_out 的向量，而 ||S||2 為 S 的L2范數(shù)。

損失函數(shù)有了，現(xiàn)在我們開始用梯度下降法迭代求解每一層的 W，b。

首先是輸出層第L層。注意到輸出層的 W，b 滿足下式：

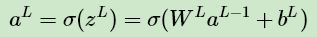
這樣對于輸出層的參數(shù)，我們的損失函數(shù)變?yōu)椋?/p>

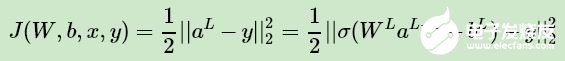
這樣求解 W，b 的梯度就簡單了：

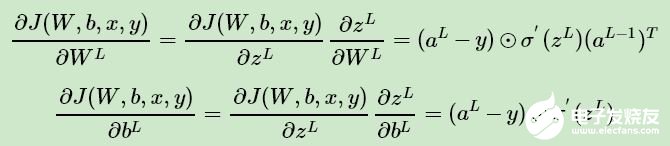
注意上式中有一個符號 ⊙，它代表Hadamard積，對于兩個維度相同的向量 A ( a1 , a2 , ... an ) T 和 B ( b1 , b2 , ... bn ) T，則 A⊙B = ( a1b1,a2b2,... anbn ) T。

我們注意到在求解輸出層的 W，b 的時候，有公共的部分

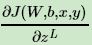
因此我們可以把公共的部分即對 zL 先算出來，記為：

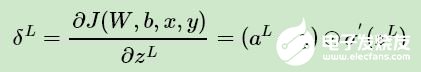
現(xiàn)在我們終于把輸出層的梯度算出來了，那么如何計算上一層 L ? 1 層的梯度，上上層 L ? 2 層的梯度呢？這里我們需要一步步的遞推，注意到對于第l層的未激活輸出 zL ，它的梯度可以表示為：

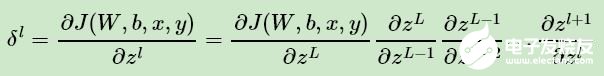
如果我們可以依次計算出第 l 層的 δl ，則該層的 Wl，bl 很容易計算？為什么呢？注意到根據(jù)前向傳播算法，我們有：

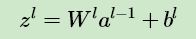
所以根據(jù)上式我們可以很方便的計算出第 l 層的 Wl，bl 的梯度如下：

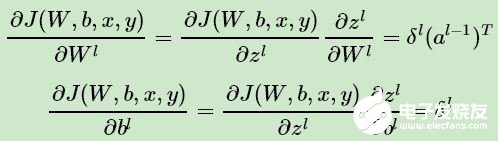
那么現(xiàn)在問題的關(guān)鍵就是要求出 δl 了。這里我們用數(shù)學(xué)歸納法，第 L 層的 δL上面我們已經(jīng)求出， 假設(shè)第 l + 1 層的 δl+1 已經(jīng)求出來了，那么我們?nèi)绾吻蟪龅?l 層的 δl 呢？我們注意到：

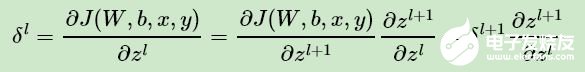
可見，用歸納法遞推 δl+1 和 δl 的關(guān)鍵在于求解

而 zl+1 和 zl 的關(guān)系其實很容易找出：

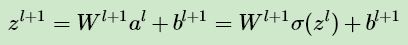
這樣很容易求出：

將上式帶入上面 δl+1 和 δl 關(guān)系式我們得到：

現(xiàn)在我們得到了δl的遞推關(guān)系式，只要求出了某一層的 δl ，求解 Wl，bl 的對應(yīng)梯度就很簡單的。

（注意，上面的矩陣求導(dǎo)推導(dǎo)部分不太嚴(yán)謹(jǐn)，定性理解即可。）

3. DNN反向傳播算法過程

現(xiàn)在我們總結(jié)下DNN反向傳播算法的過程。由于梯度下降法有批量（Batch），小批量(mini-Batch)，隨機三個變種，為了簡化描述，這里我們以最基本的批量梯度下降法為例來描述反向傳播算法。實際上在業(yè)界使用最多的是mini-Batch的梯度下降法。不過區(qū)別僅僅在于迭代時訓(xùn)練樣本的選擇而已。

輸入: 總層數(shù) L ，以及各隱藏層與輸出層的神經(jīng)元個數(shù)，激活函數(shù)，損失函數(shù)，迭代步長 α，最大迭代次數(shù)MAX與停止迭代閾值 ?，輸入的 m 個訓(xùn)練樣本{ ( x1 , y1 ) , ( x2 , y2 ) , ... , ( xm , ym ) }

輸出：各隱藏層與輸出層的線性關(guān)系系數(shù)矩陣 W 和偏倚向量 b

1) 初始化各隱藏層與輸出層的線性關(guān)系系數(shù)矩陣 W 和偏倚向量 b 的值為一個隨機值。

2）for iter to 1 to MAX：

2-1) for i = 1 to m：

a) 將DNN輸入 a1 設(shè)置為 xi
b) for l = 2 to L，進(jìn)行前向傳播算法計算

c) 通過損失函數(shù)計算輸出層的 δi,L
d) for l= L-1 to 2, 進(jìn)行反向傳播算法計算

2-2) for l = 2 to L，更新第 l 層的 Wl，Wl，bl：

2-3) 如果所有 W，b 的變化值都小于停止迭代閾值 ?，則跳出迭代循環(huán)到步驟3。

3） 輸出各隱藏層與輸出層的線性關(guān)系系數(shù)矩陣 W 和偏倚向量 b 。

4. DNN反向傳播算法小結(jié)

有了DNN反向傳播算法，我們就可以很方便的用DNN的模型去解決第一節(jié)里面提到了各種監(jiān)督學(xué)習(xí)的分類回歸問題。當(dāng)然DNN的參數(shù)眾多，矩陣運算量也很大，直接使用會有各種各樣的問題。有哪些問題以及如何嘗試解決這些問題并優(yōu)化DNN模型與算法，我們在下一篇講。

編輯：jq