本文旨在優化一維函數,實際上模型參數有數百萬維以上,差距很大,因此本文最好作為輔助法的理解,而非對算法優劣的判斷依據。 在深度學習中,有很多種優化算法,這些算法需要在極高維度(通常參數有數百萬個以上)也即數百萬維的空間進行梯度下降,從最開始的初始點開始,尋找最優化的參數,通常這一過程可能會遇到多種的情況,諸如: 1、提前遇到局部最小值從而卡住,再也找不到全局最小值了。 2、遇到極為平坦的地方:“平原”,在這里梯度極小,經過多次迭代也無法離開。同理,鞍點也是一樣的,在鞍點處,各方向的梯度極小,盡管沿著某一個方向稍微走一下就能離開。 3、“懸崖”,某個方向上參數的梯度可能突然變得奇大無比,在這個地方,梯度可能會造成難以預估的后果,可能讓已經收斂的參數突然跑到極遠地方去。 為了可視化&更好的理解這些優化算法,我首先拼出了一個很變態的一維函數: 其導數具有很簡單的形式: 具體長得像:
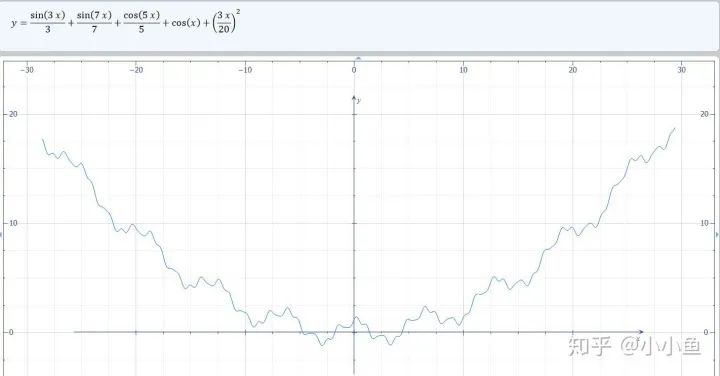
具有懸崖和大量的局部最小值,足以模擬較為復雜的優化情況了。
算法1:純粹的梯度下降法 該算法很簡單,表述如下:
首先給出學習率lr,初始x while True: x = x - lr*df/dx 根據學習率的不同,可以看到不同的效果。學習率過小,卡在局部極小值,學習率過大,壓根不收斂。
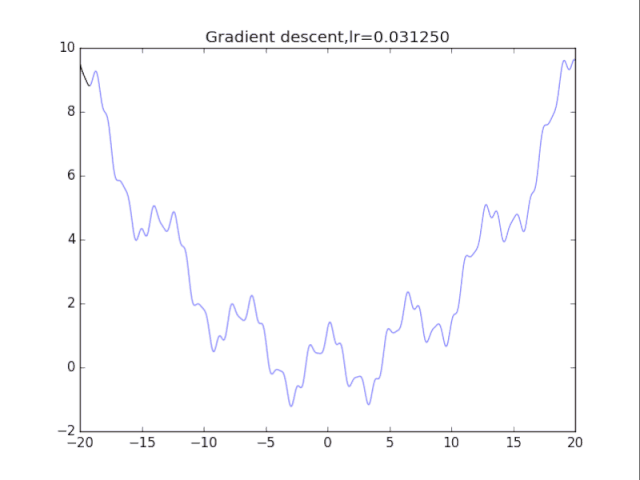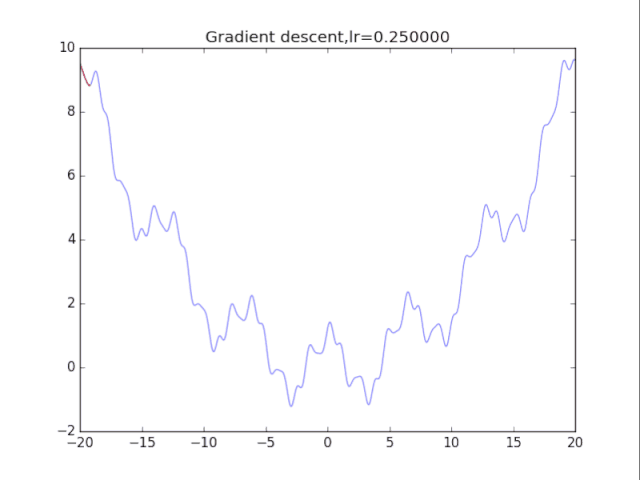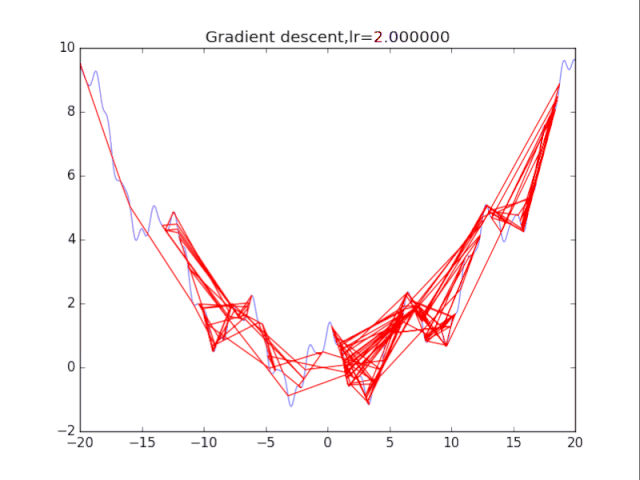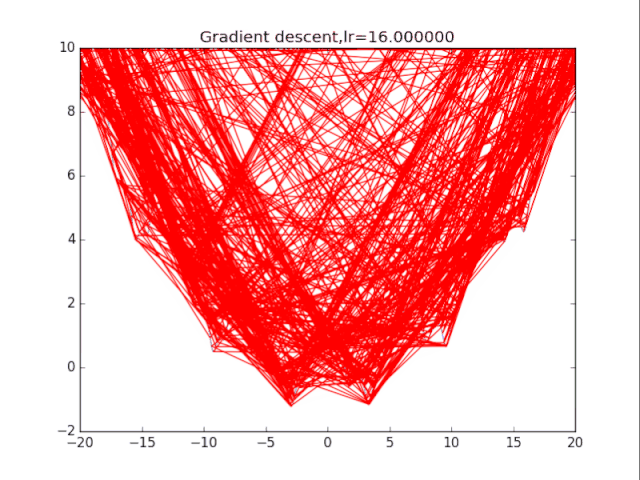
梯度下降法
算法2:梯度下降法+動量 算法在純粹的梯度下降法之上,外加了梯度,從而記錄下了歷史的梯度情況,從而減輕了卡在局部最小值的危險,在梯度=0的地方仍然會有一定的v剩余,從而在最小值附近搖擺。
首先給出學習率lr,動量參數m 初始速度v=0,初始x while True: v = m * v - lr * df/dx x += v 下面可以看圖:
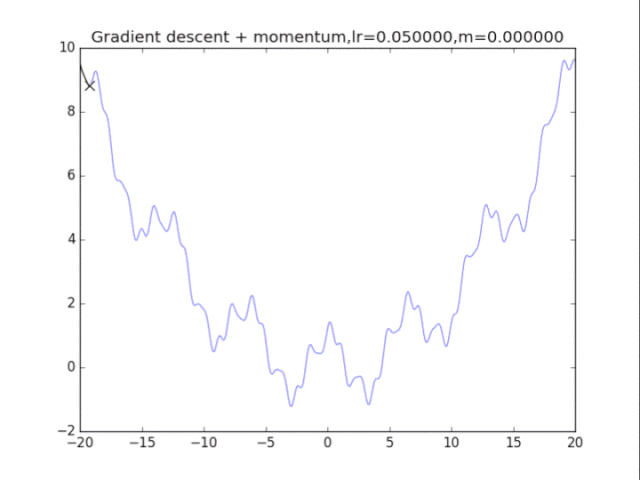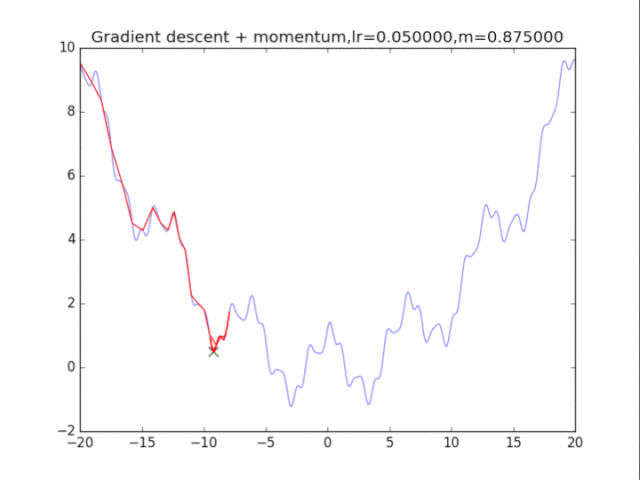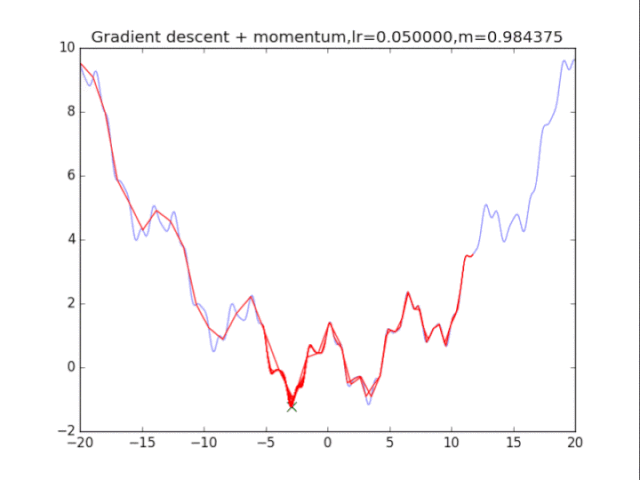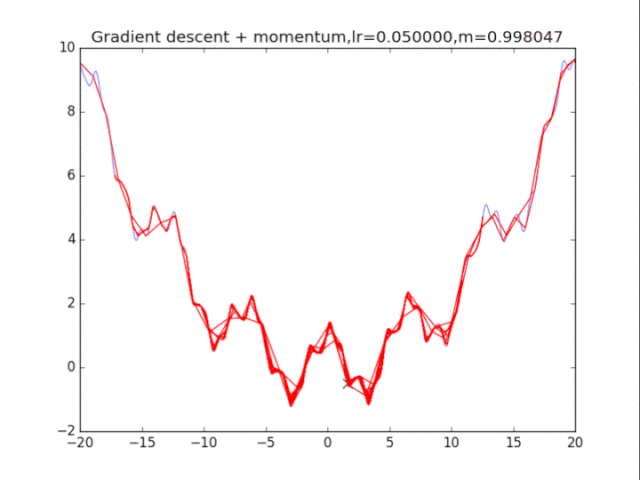
梯度下降+動量, lr=0.05
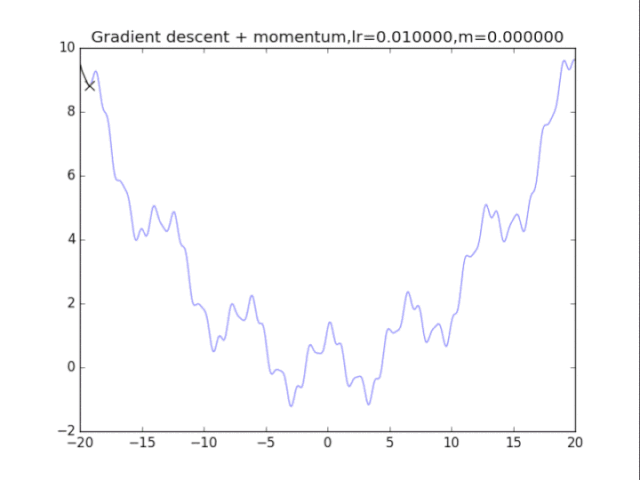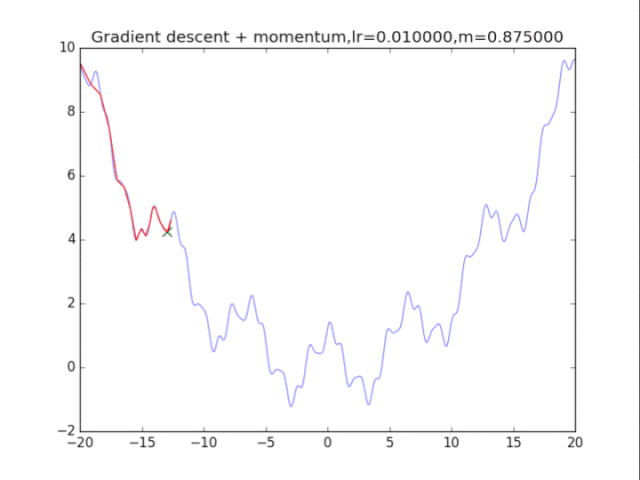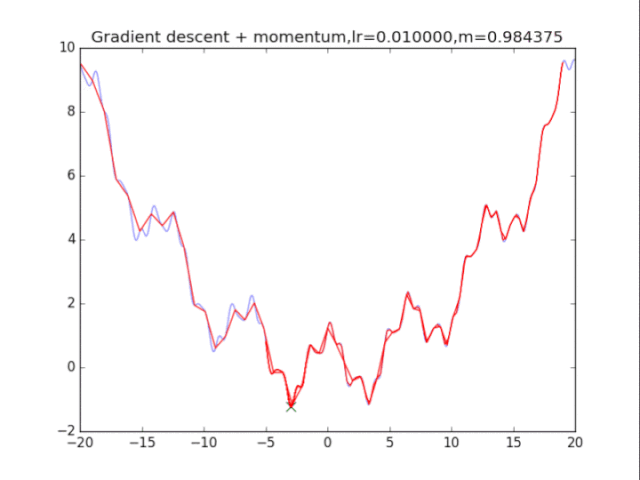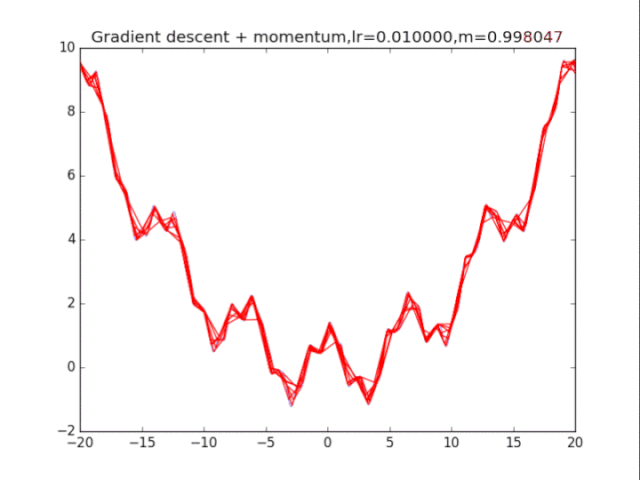
梯度下降+動量, lr=0.01
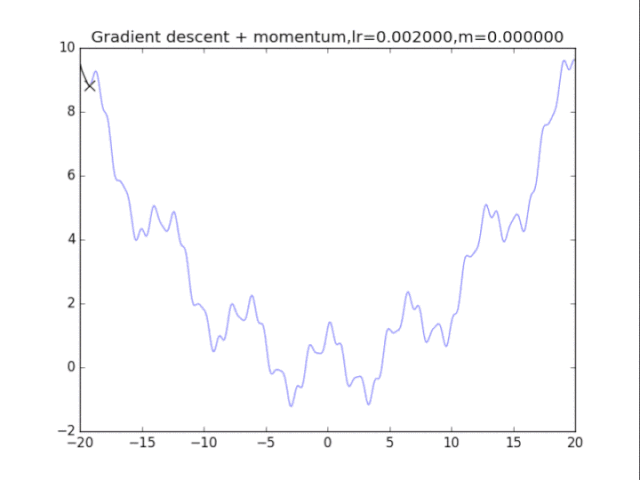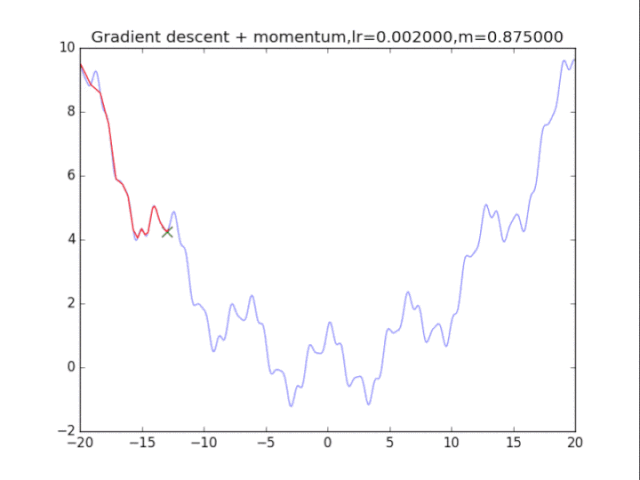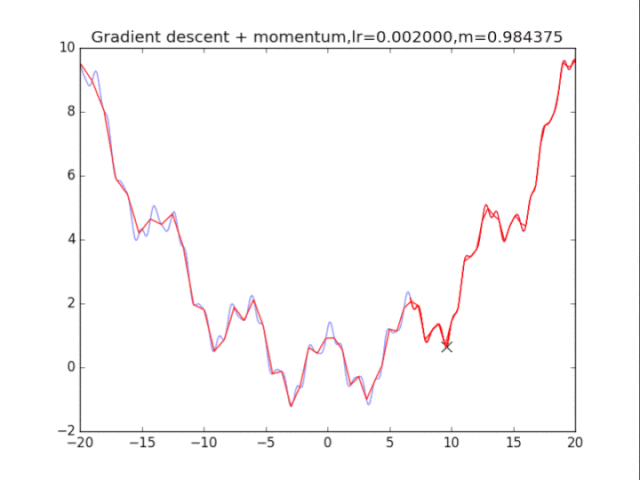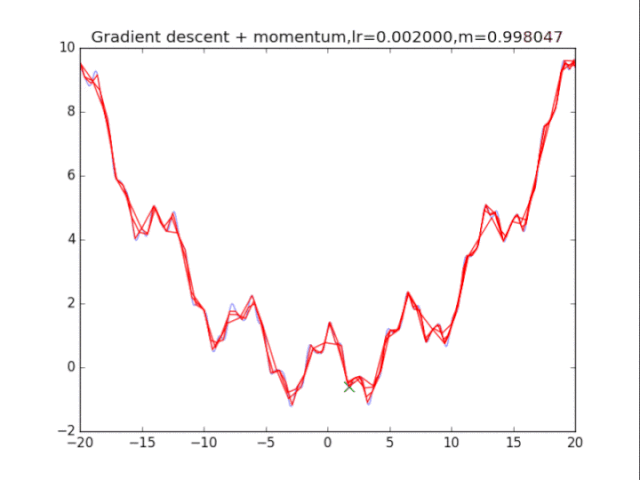
梯度下降+動量, lr=0.002 從中我們可以看出: 1、lr越小越穩定,太大了很難收斂到最小值上,但是太小的話收斂就太慢了。 2、動量參數不能太小,0.9以上表現比較好,但是又不能太大,太大了無法停留在最小值處。
算法3:AdaGrad算法 AdaGrad算法的思想是累計歷史上出現過的梯度(平方),用積累的梯度平方的總和的平方根,去逐元素地縮小現在的梯度。某種意義上是在自行縮小學習率,學習率的縮小與過去出現過的梯度有關。 缺點是:剛開始參數的梯度一般很大,但是算法在一開始就強力地縮小了梯度的大小,也稱學習率的過早過量減少。 算法描述:
給出學習率lr,delta=1e-7累計梯度r=0,初始xwhile True: g = df/dx r = r + g*g x = x - lr / (delta+ sqrt(r)) * g
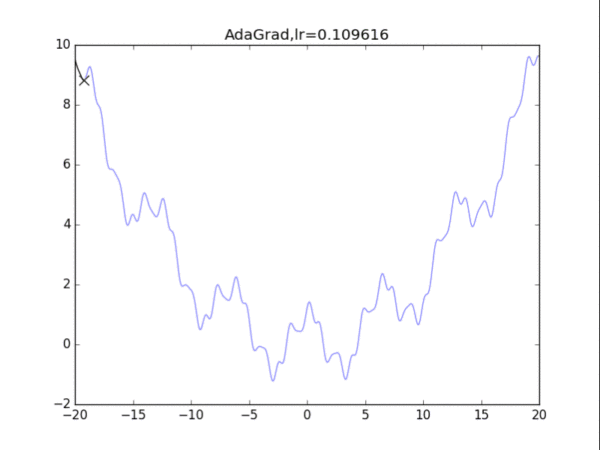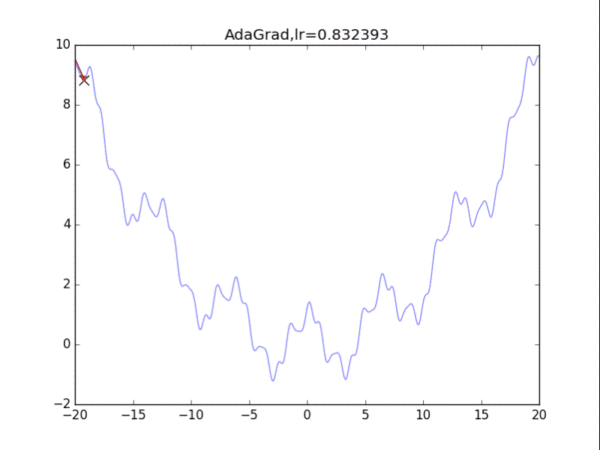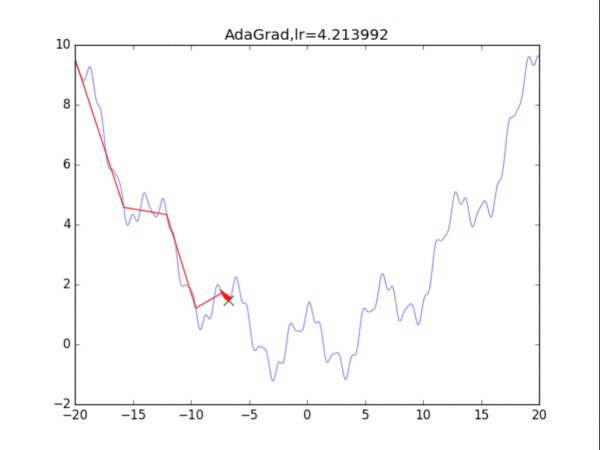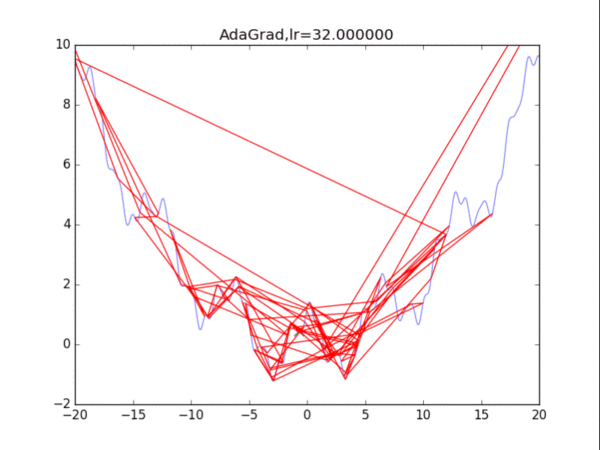
效果并不是很好......
算法4:RMSProp AdaGrad算法在前期可能會有很大的梯度,自始至終都保留了下來,這會使得后期的學習率過小。RMSProp在這個基礎之上,加入了平方梯度的衰減項,只能記錄最近一段時間的梯度,在找到碗狀區域時能夠快速收斂。 算法描述:
給出學習率lr,delta=1e-6,衰減速率p累計梯度r=0,初始xwhile True: g = df/dx r = p*r + (1-p)*g*g x = x - lr / (delta+ sqrt(r)) * g
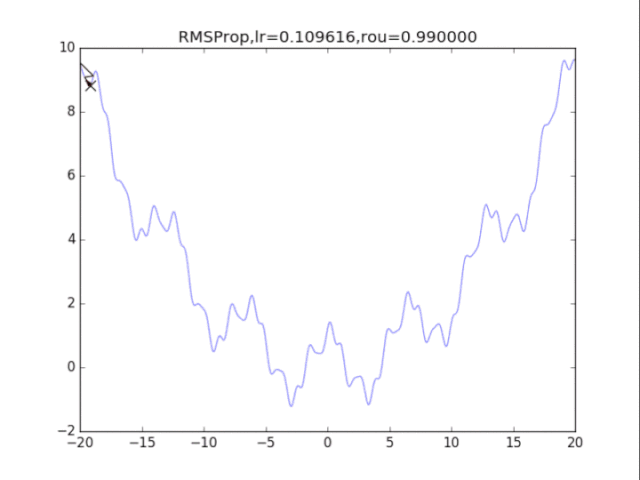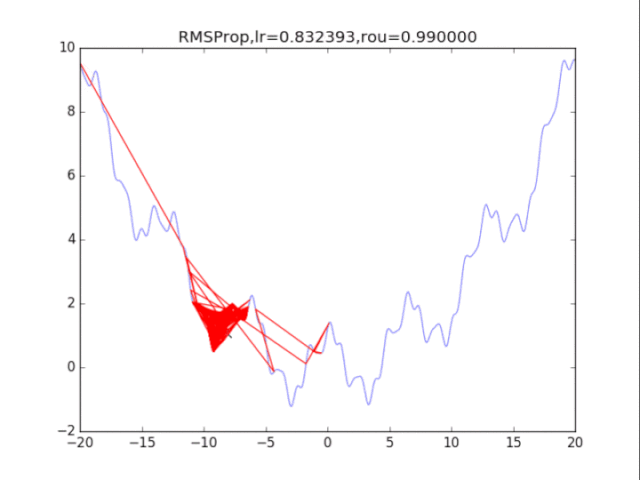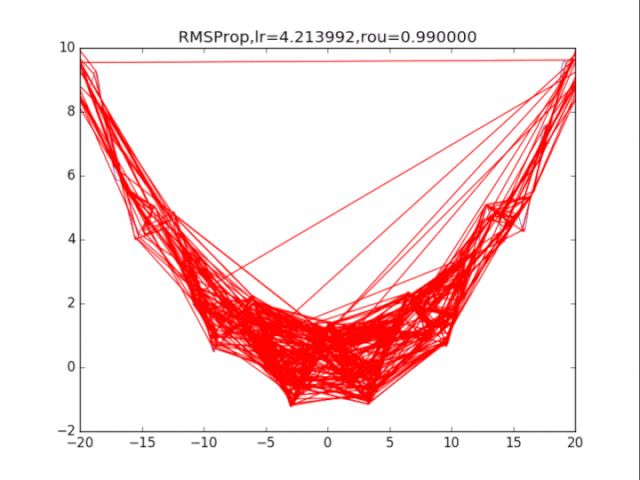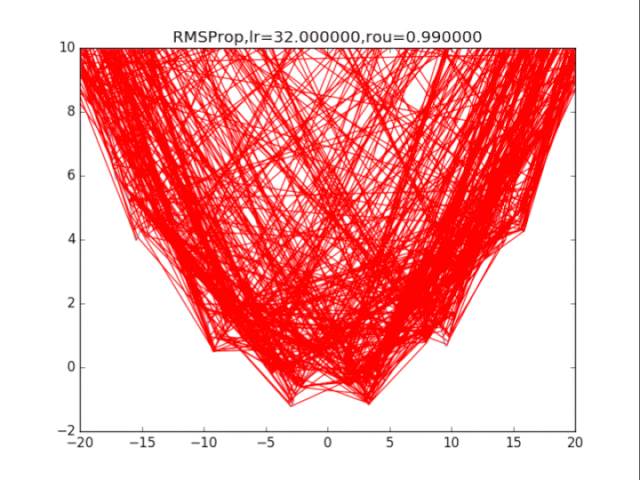
RMSProp,p=0.99
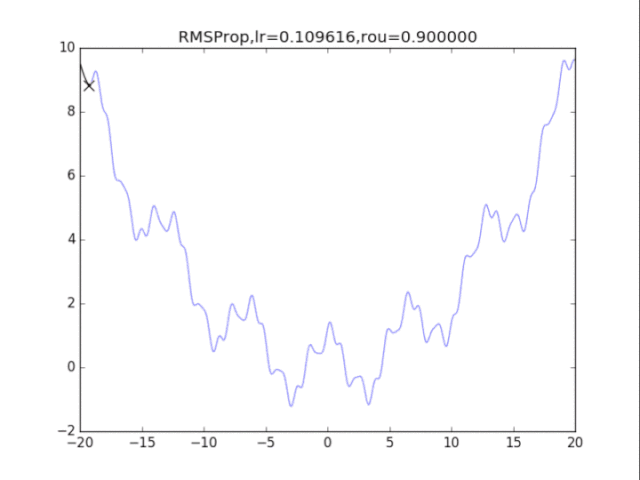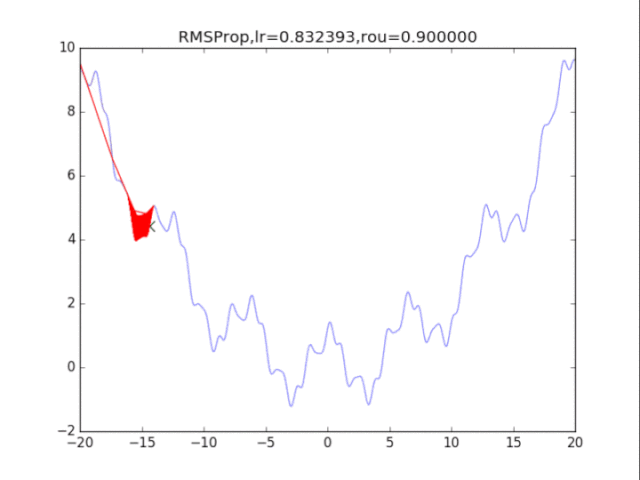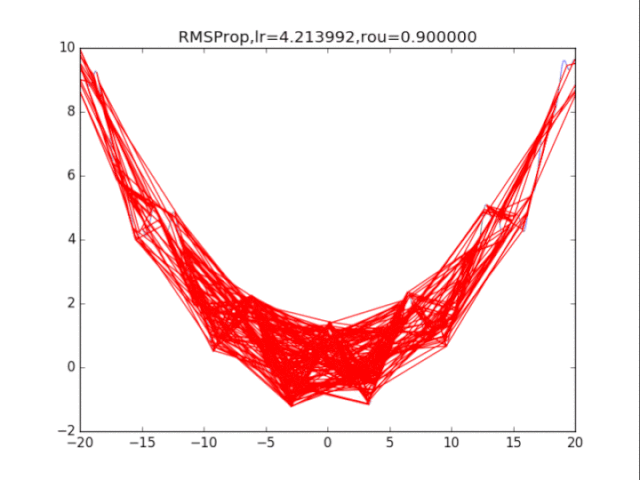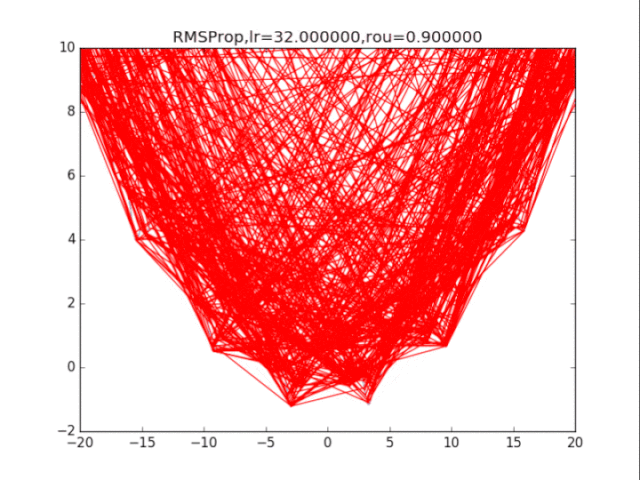
RMSProp,p=0.9
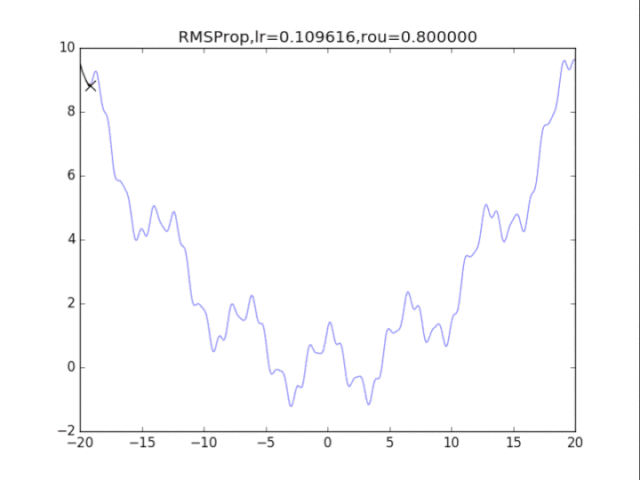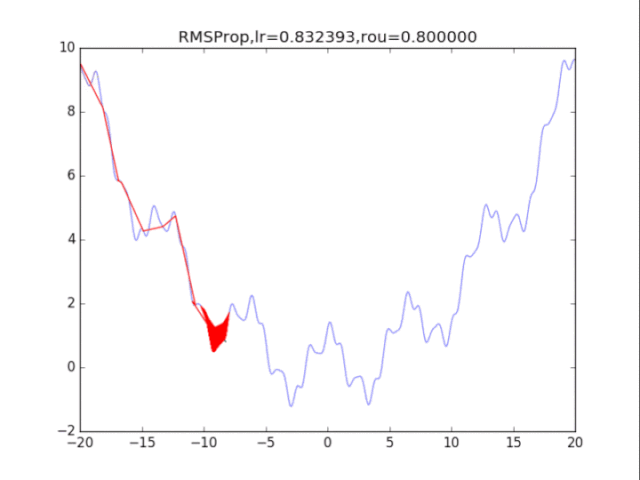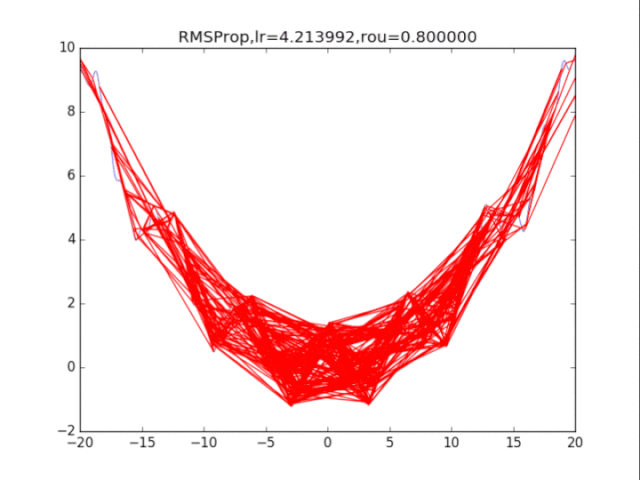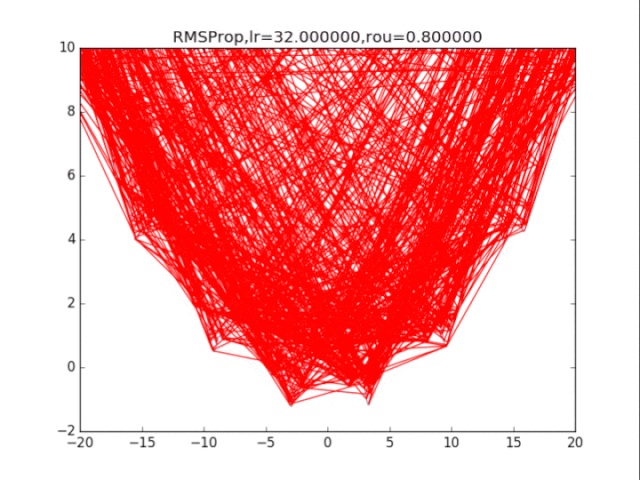
RMSProp,p=0.8 衰減速率情況復雜,建議自行調參.......
算法5:Adam算法 Adam算法和之前類似,也是自適應減少學習率的算法,不同的是它更新了一階矩和二階矩,用一階矩有點像有動量的梯度下降,而用二階矩來降低學習率。 此外還使用了類似于s = s / (1-p1^t)這樣的公式,這樣的公式在t較為小的時候會成倍增加s,從而讓梯度更大,參數跑的更快,迅速接近期望點。而后續t比較大的時候,s = s / (1-p1^t)基本等效于s=s,沒什么用。 算法如下:
給出學習率lr,delta=1e-8,衰減速率p1=0.9,p2=0.999 累計梯度r=0,初始x ,一階矩s=0,二階矩r=0時間t = 0while True: t += 1 g = df/dx s = p1*s + (1-p1) *g r = p2*r +(1-p2)*g*g s = s / (1-p1^t) r = r / (1-p2^t) x = x - lr / (delta+ sqrt(r)) * s
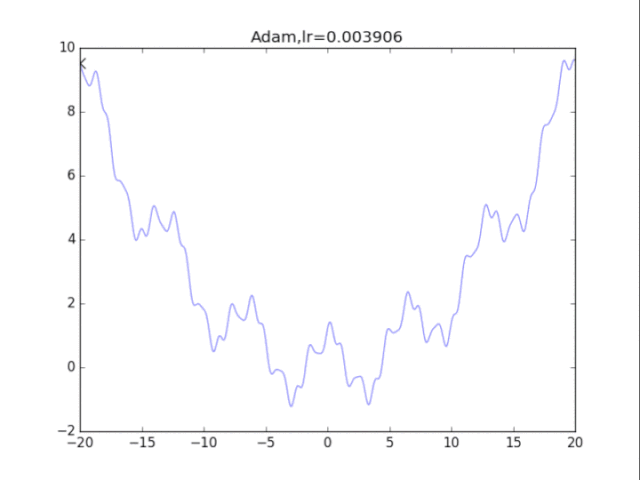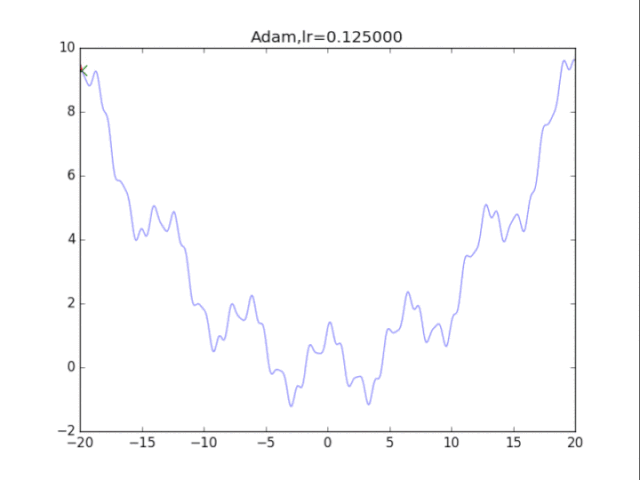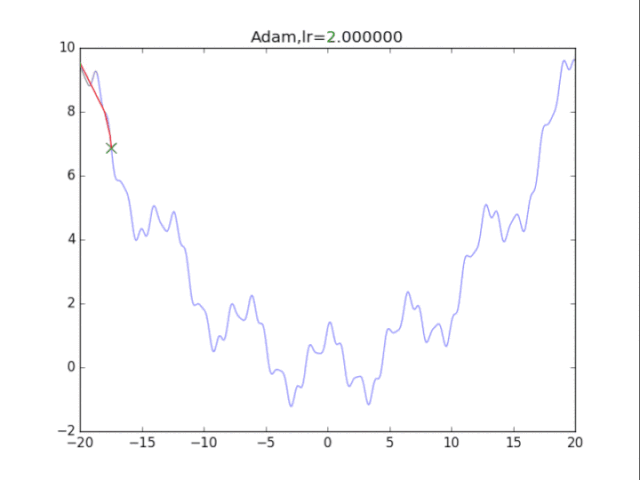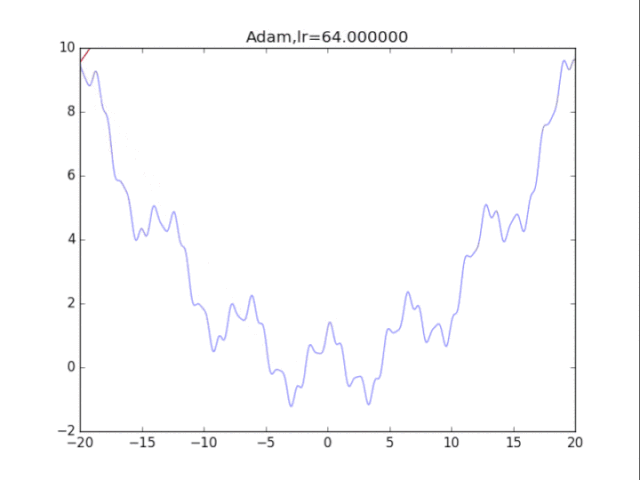
Adam算法,鬼一樣的表現 是的,你沒有看錯,這玩意壓根不收斂......表現極差。 在算法中仔細研究后才發現,是在t很小的前幾步的時候,p2=0.999太大了,導致r = r / (1-p2^t) 中,1-p2^t接近0,r迅速爆炸,百步之內到了inf。后來修改p2=0.9后效果就好得多了。
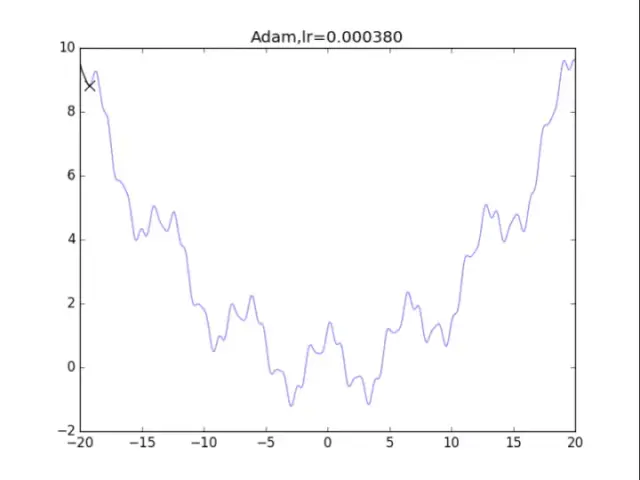
Adam算法,神級表現 最后還是Adam效果最好了 :),盡管學習率還是需要相當的調參。
算法6:牛頓法 牛頓法是二階近似方法的一種,其原理類似于將某函數展開到二次方(二次型)項: 如果幸運的話,這個展開式是一個開口向上的曲面,一步就走到這個曲面的最低點:
初始x while True: g = df(x) # 一階導數 gg = ddf(x) # 二階導數 x = x - g/gg # 走到曲面的最低點
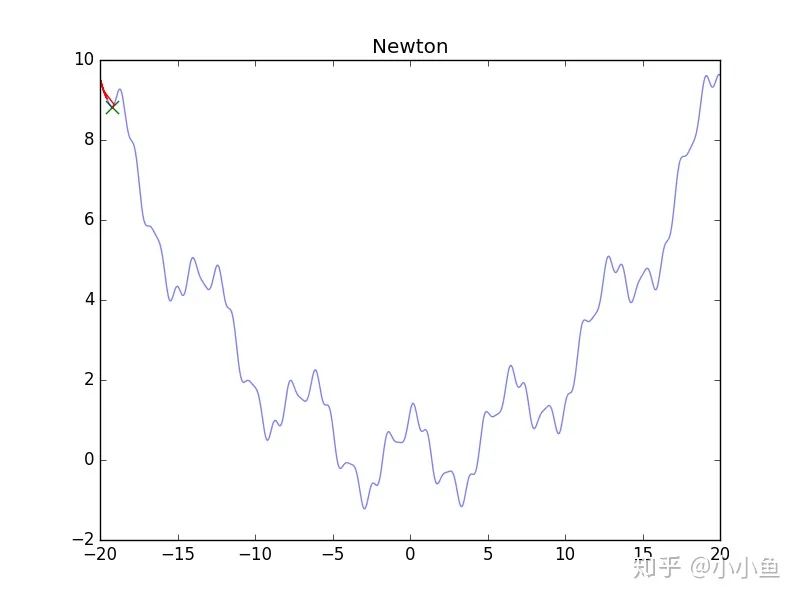
可憐的牛頓法,靜態圖 圖片如上,看了真可憐........其實牛頓法要求的是H矩陣正定(一維情況下是二階導數大于零),在多維中,這樣的情況難以滿足,大量出現的極小值,懸崖,鞍點都會造成影響,導致無法順利進行下去,為了更好地進行牛頓法,我們需要正則化它。
算法7:牛頓法+正則化 牛頓法加上正則化可以避免卡在極小值處,其方法也很簡單:更新公式改成如下即可。 一維的算法如下:
初始x ,正則化強度alphawhile True: g = df(x) # 一階導數 gg = ddf(x) # 二階導數 x = x - g/(gg+alpha) # 走到曲面的最低點 效果圖:
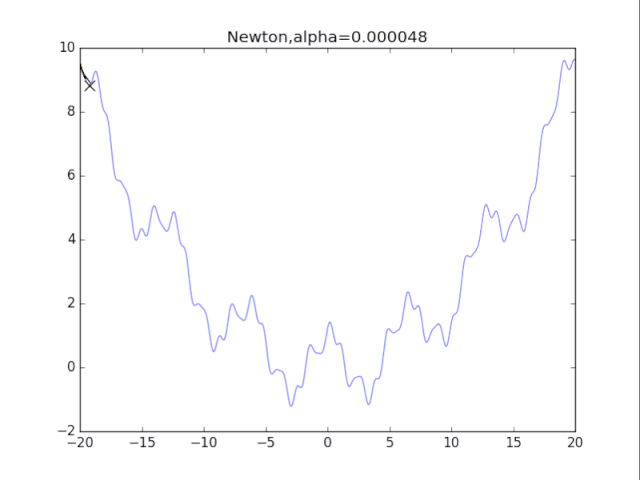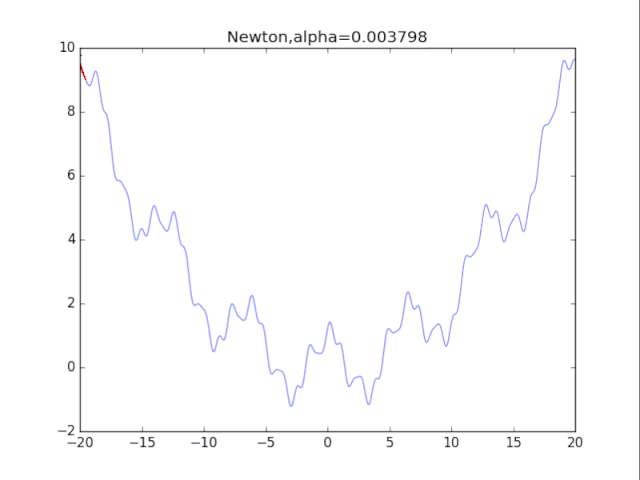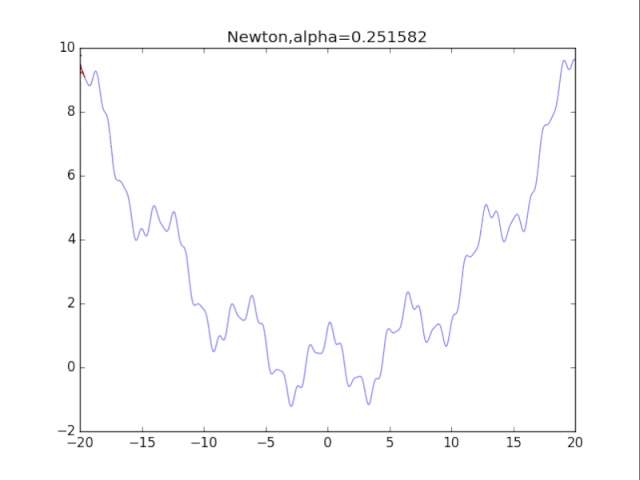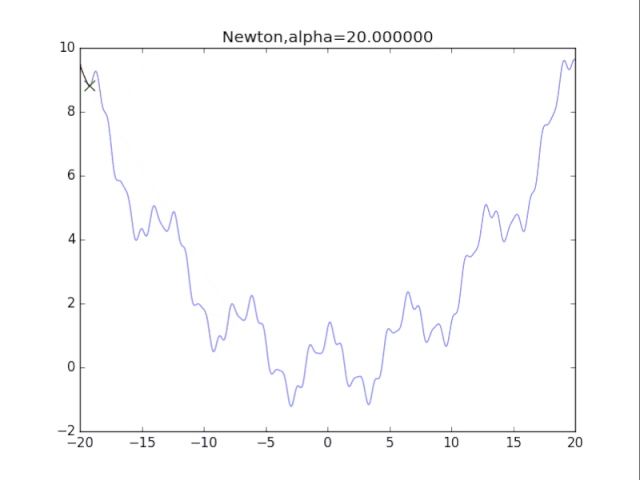
牛頓法+正則化 看了真可憐.........二次方法真心在非凸情況很糟糕。此外算法涉及H矩陣的逆,這需要O(n^3)的計算量,非深度學習可用。 參考文獻 [1]Ian Goodfellow,深度學習Deep Learning,人民郵電出版社,170-190 代碼
#coding:utf-8from __future__ import print_functionimport numpy as npimport matplotlib.pyplot as plt def f(x): return (0.15*x)**2 + np.cos(x) + np.sin(3*x)/3 + np.cos(5*x)/5 + np.sin(7*x)/7 def df(x): return (9/200)*x - np.sin(x) -np.sin(5*x) + np.cos(3*x) + np.cos(7*x) points_x = np.linspace(-20, 20, 1000)points_y = f(points_x) # 純粹的梯度下降法,GDfor i in range(10): # 繪制原來的函數 plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-") # 算法開始 lr = pow(2,-i)*16 x = -20.0 GD_x, GD_y = [], [] for it in range(1000): GD_x.append(x), GD_y.append(f(x)) dx = df(x) x = x - lr * dx plt.xlim(-20, 20) plt.ylim(-2, 10) plt.plot(GD_x, GD_y, c="r", linestyle="-") plt.title("Gradient descent,lr=%f"%(lr)) plt.savefig("Gradient descent,lr=%f"%(lr) + ".png") plt.clf() # 動量 + 梯度下降法for i in range(10): # 繪制原來的函數 plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-") # 算法開始 lr = 0.002 m = 1 - pow(0.5,i) x = -20 v = 1.0 GDM_x, GDM_y = [], [] for it in range(1000): GDM_x.append(x), GDM_y.append(f(x)) v = m * v - lr * df(x) x = x + v plt.xlim(-20, 20) plt.ylim(-2, 10) plt.plot(GDM_x, GDM_y, c="r", linestyle="-") plt.scatter(GDM_x[-1],GDM_y[-1],90,marker = "x",color="g") plt.title("Gradient descent + momentum,lr=%f,m=%f"%(lr,m)) plt.savefig("Gradient descent + momentum,lr=%f,m=%f"%(lr,m) + ".png") plt.clf() # AdaGradfor i in range(15): # 繪制原來的函數 plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-") # 算法開始 lr = pow(1.5,-i)*32 delta = 1e-7 x = -20 r = 0 AdaGrad_x, AdaGrad_y = [], [] for it in range(1000): AdaGrad_x.append(x), AdaGrad_y.append(f(x)) g = df(x) r = r + g*g # 積累平方梯度 x = x - lr /(delta + np.sqrt(r)) * g plt.xlim(-20, 20) plt.ylim(-2, 10) plt.plot(AdaGrad_x, AdaGrad_y, c="r", linestyle="-") plt.scatter(AdaGrad_x[-1],AdaGrad_y[-1],90,marker = "x",color="g") plt.title("AdaGrad,lr=%f"%(lr)) plt.savefig("AdaGrad,lr=%f"%(lr) + ".png") plt.clf() # RMSPropfor i in range(15): # 繪制原來的函數 plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-") # 算法開始 lr = pow(1.5,-i)*32 delta = 1e-6 rou = 0.8 x = -20 r = 0 RMSProp_x, RMSProp_y = [], [] for it in range(1000): RMSProp_x.append(x), RMSProp_y.append(f(x)) g = df(x) r = rou * r + (1-rou)*g*g # 積累平方梯度 x = x - lr /(delta + np.sqrt(r)) * g plt.xlim(-20, 20) plt.ylim(-2, 10) plt.plot(RMSProp_x, RMSProp_y, c="r", linestyle="-") plt.scatter(RMSProp_x[-1],RMSProp_y[-1],90,marker = "x",color="g") plt.title("RMSProp,lr=%f,rou=%f"%(lr,rou)) plt.savefig("RMSProp,lr=%f,rou=%f"%(lr,rou) + ".png") plt.clf() # Adamfor i in range(48): # 繪制原來的函數 plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-") # 算法開始 lr = pow(1.2,-i)*2 rou1,rou2 = 0.9,0.9 # 原來的算法中rou2=0.999,但是效果很差 delta = 1e-8 x = -20 s,r = 0,0 t = 0 Adam_x, Adam_y = [], [] for it in range(1000): Adam_x.append(x), Adam_y.append(f(x)) t += 1 g = df(x) s = rou1 * s + (1 - rou1)*g r = rou2 * r + (1 - rou2)*g*g # 積累平方梯度 s = s/(1-pow(rou1,t)) r = r/(1-pow(rou2,t)) x = x - lr /(delta + np.sqrt(r)) * s plt.xlim(-20, 20) plt.ylim(-2, 10) plt.plot(Adam_x, Adam_y, c="r", linestyle="-") plt.scatter(Adam_x[-1],Adam_y[-1],90,marker = "x",color="g") plt.title("Adam,lr=%f"%(lr)) plt.savefig("Adam,lr=%f"%(lr) + ".png") plt.clf() # 牛頓法for i in range(72): # 繪制原來的函數 plt.plot(points_x, points_y, c="b", alpha=0.5, linestyle="-") # 算法開始 alpha= pow(1.2,-i)*20 x = -20.0 Newton_x, Newton_y = [], [] for it in range(1000): Newton_x.append(x), Newton_y.append(f(x)) g = df(x) gg = ddf(x) x = x - g/(gg+alpha) plt.xlim(-20, 20) plt.ylim(-2, 10) plt.plot(Newton_x, Newton_y, c="r", linestyle="-") plt.scatter(Newton_x[-1],Newton_y[-1],90,marker = "x",color="g") plt.title("Newton,alpha=%f"%(alpha)) plt.savefig("Newton,alpha=%f"%(alpha) + ".png") plt.clf()
-
算法
+關注
關注
23文章
4619瀏覽量
93039 -
可視化
+關注
關注
1文章
1197瀏覽量
20966 -
深度學習
+關注
關注
73文章
5507瀏覽量
121266
原文標題:深度學習中7種最優化算法的可視化與理解
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 深度學習中多種優化算法
深度學習中多種優化算法

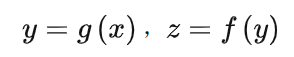











評論