T-S-T三級交換網絡路徑搜索算法的研究

　　1 引 言

　　光纖通訊技術的飛速發展使得目前高速通訊網絡性能的瓶頸集中在高速交換系統，研究、設計和制造高速交換系統對目前高速通訊網絡具有極其重要的意義。而且隨著電信網和計算機網絡的高速發展，高速大容量的交叉連接或交換設備和芯片的性能也在大幅度的提高。同時由于現在的交換機在不停地更新換代，對新的交換算法的需求也在不斷增加。

　　本文的研究工作旨在利用矩陣置換的思想，模擬開發一種基于T(時分)-S(空分)-T(時分)交換網絡的調度算法。提出一種新的三級交換的矩陣模型，并在這種模型上設計相應的無阻塞交換算法。利用矩陣作為數學模型，可以利用矩陣的置換操作搜索交換的設置。算法設計和實現的過程中，大量的實驗表明，本算法具有良好的特性，而且通過芯片級聯可實現。

　　本算法不同于以往的基于圖論的尋徑調度算法，力圖通過對這個算法的研究，為未來的大型綜合數字交換網絡奠定理論和實踐基礎，并為變化多端的網絡環境下快速建立有保障的網絡服務提供先期的技術研究。

　　2 T-S-T數字交換網絡結構

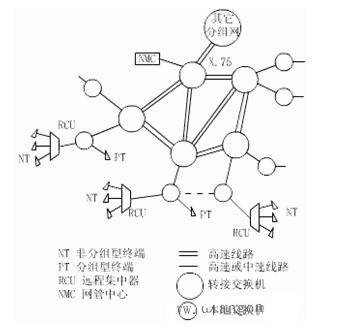
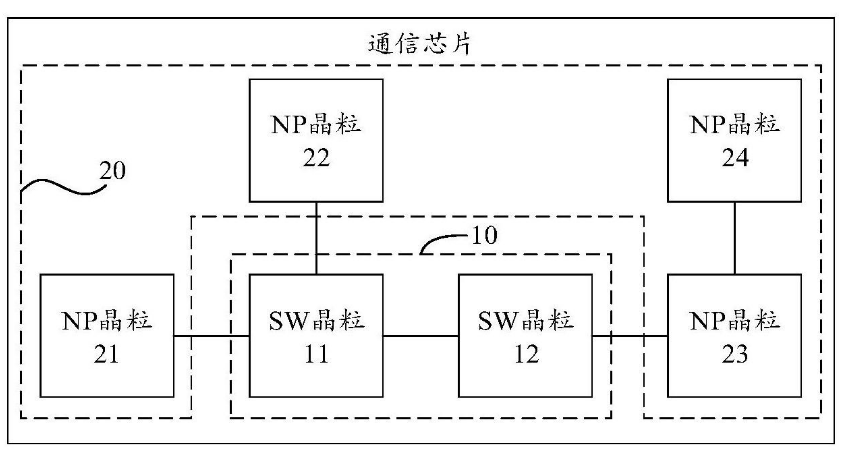
　　典型的T-S-T數字交換網絡可以用圖1的模型描述。

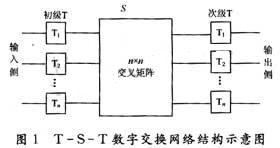
　　整個交換網絡以S接線器為核心組織。對于一個具有N條輸入復用線和N條輸出復用線的交換網絡而言，需要配置2N套T接線器，其中N套在輸入側，為初級T接線器，完成用戶的發送時隙到交換網絡內部的公共時隙的交換；N套在輸出側，稱為次級T接線器，完成將交換網絡內部的公共時隙上的住處傳送到另一用戶的接收時隙上。因此，交換網絡內部提供的公共時隙的數量就決定了交換網絡中能夠形成的話音通路的數量。中間的S接線器主要由一個N×N的交叉接點和具有N個存儲器的控制存儲器組來組成，用來完成將交換網絡內部運載的用戶信息從一條輸入側復用線上交換到規定的一條輸出復用線上。

　　3 T-S-T交換網絡數學模型的建立

　　3.1 問題的描述

　　在建立T-S-T交換網絡的數學模型之前，首先給出這樣的數學抽象：用1個n×n的輸入矩陣inport表示輸入數據流，每一行代表1個T-S-T交換網絡的輸入鏈路，也就是說每一行代表l根鏈路HW，每一行內元素的位置代表1個時隙內各個數據幀的次序關系。由于T交換是對同一根鏈路的不同時隙之間進行的交換，故將其抽象為矩陣的行內置換。因此當輸入矩陣inport經過一級T交換后，得到1個中間矩陣after_t1，此矩陣是inport矩陣通過每一行數據的行內變換得到。同理，由于S交換是在不同鏈路的相同時隙之間進行的交換，類似于對一個矩陣在其同一列內進行列內變換，稱其為列內置換。這樣當 after_tl又經過S交換，得到另外一個中間矩陣after_s，此矩陣是after_tl矩陣通過列內變換得到的。最后，又經過第二級的T交換，產生outport矩陣，類似地，他是after_s矩陣通過行內變換得到。于是，可以將交換算法這樣描述：對于初始矩陣inport，怎樣能找到一種滿足 T-S-T三級交換的變換方式，最終得到1個輸出矩陣outport。而且對于用戶要求的任意outport(此矩陣與inport是單播關系)，都可以通過算法找到其變換方式，即可以找到2個中間矩陣。

　　3.2 矩陣模型的建立

　　將T變換對應于矩陣的行內變換，而S變換對應于矩陣的列內變換，這樣上面的這一段敘述就可以描述為inport矩陣經過一系列的行內變換得到after_t1矩陣，after_t1矩陣經過一系列的列內變換得到after_s矩陣，after_s矩陣又經過一系列的行內變換得到outport矩陣如圖2所示。

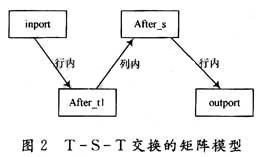
　　4 交換算法的設計思想

　　從上面論述可以看到，本文已經將具體的路徑選擇問題，抽象成純粹的數學問題。接下來，本文將從純數學的角度來找出一種算法，從而解決這個交換問題。

　　4.1 問題的數學分析

　　觀察從輸入矩陣inport→中間矩陣after_t1→中間矩陣after_s→輸出矩陣outport整個的變換過程，輸入矩陣先后經過2次時間變換，而只經過1次空間變換。也就是說，當輸入矩陣inport中的某個元素，要發生列變換時，他只有1次變換機會，此情況對于inport中的任意一個元素都是適用的。所以，時間變換只起到調整作用，因此本文要重點考察空間變換，試圖從空間變換S變換中找出矩陣的特點。

　　不難發現，中間矩陣 after_s(n×m)(一般情況下，本文取m=n，無阻塞的交換網絡)有這樣的特點：每一列的n個元素，他們的行號包含從1～n的所有行號。如上面的例子可以看到這一點。這樣，將after_s矩陣經過1個空間變換，向空間變換的反方向變換的時候，這n個元素就會回到在inport矩陣原來的行上，在經過1個時間變換的反變換就可以變成為輸入矩陣inport。

　在發現中間矩陣after_s的特點之后，就有了基本的思路。這里的算法只要能夠使得outport矩陣經過1個時間變換的反變換后能夠變成為滿足中間矩陣after_s的特點的矩陣，那么，也就找到一種矩陣的變換方式。解決了這個交換問題。有沒有一個從inport到outport的變換的問題，轉換成能不能找到一個滿足after_s矩陣要求的問題，此after_s矩陣只是 outport矩陣經過一個時間變換得到。

　　這樣，對于任意輸入矩陣inpott，經過矩陣的行內、列內、行內3次變換可以得到任意輸出矩陣 outport，從而成功的完成了T-S-T交換。本文為了方便描述inport和T-S-T交換的核心算法，不妨將inport定義為順序矩陣n×n，就是以行為序，從0～n×n-1，例如n=4，inport被定義為：

　　而outport將是inport的任意置換矩陣。在這里也不妨將outport假設為：

　　為了從inport矩陣變換到outport矩陣，必須找到兩個中間矩陣after_t1和after_s，從而完成交換路徑的接續。因此本文的目標是研究一種算法，根據輸入矩陣和輸出矩陣產生這兩個中間矩陣，從而使處理機可以根據4個矩陣往寄存器陣列中填值，這樣就可以實現T-S-T網絡交換。為了以后敘述方便，3個寄存器陣列定義為：Tregister1(時分)、Sregister(空分)、Tregister2(時分)。

　　由于在實際的 T-S-T交換中，CPU根據各個控制寄存器中的值來完成交換。由交換的特點可知，每個控制寄存器的值是由輸入序列和輸出序列決定的。其中 Tregisterl的值可以由inport和after_t1決定，同理，Sregister的值由after_t1和after_s決定，Tregister2的值由after_s和outport決定。

　　4.2 算法思想的設計

　　算法設計要求：

　　(1)對于任意給定的輸入矩陣和輸出矩陣，都能夠得到2個中間矩陣；

　　(2)由輸入矩陣到第一個中間矩陣只能經過一系列行內置換；

　　(3)由第一個中間矩陣到第二個中間矩陣只能經過一系列列內置換；

　　(4)由第二個中間矩陣到輸出矩陣只能經過一系列行內置換。

　　由行內變換和列內變換的性質可以推斷出after_t1(AT)和after_s(AS)矩陣的特點如下：

　　AT的特點：ATij=INij'(只能在同一行上進行置換)；AS的特點：AS是inport的一個置換矩陣；AS的同一列上不可能出現inport同一行上的元素。

　　這是由于AT同一列上不可能出現inport同一行上的元素，而AT到AS經過的是列內變換。

　　現在有了inport和outport，目標是通過這2個矩陣找到after_t1和after_s。從上面的設計要求和模型2個中間矩陣的特點可以看出，由inport到outport所經過的置換與由outport到inport所經過的置換是對稱的，所以由outport到inpott置換所得的2個中間矩陣也是問題的解。而且inport相對于output較為確定，因此為了方便描述和算法實現，本文采用逆推法，由outport經過一系列的行內變換逆推出after_s，由after_s經過一系列的列內變換逆推出after_t1。很容易發現從after_s到after_t1只需要一個簡單的排序就可以完成，因此算法的關鍵是由outport推導after_s。

　　這樣本文研究的交換網絡調度算法要解決的關鍵問題等效后分解為：將一個任意置換矩陣經過一系列的行內變換變成為同一列上不存在輸入矩陣的同一行數據的置換矩陣(這是由AS的特點所決定的)。將解決這個關鍵問題的算法稱為交換網絡調度算法的核心算法。

　　5 關鍵矩陣算法的思想和步驟

　　5.1 高沖突值行優先排列算法

　　一些約定和定義：

　　規則：矩陣after_s同一列上不存在矩陣inport同一行上的數據。

　　那么對于任一給定輸出矩陣outport(OP)，本算法的任務是；根據“規則”將outport的每一行元素放到after_s(AS)同行的適當位置上。例如假設現在開始第i行的排列，也就是說，第0行到第i～l行的數據已經初步放置完畢(考慮到回溯，所以說“初步”)，則前i行的每一列元素的初始矩陣行可以組成1個一維矩陣，一共n個一維矩陣，定義為垂直行陣v[0]，v[1]。…，v[n一1]；而OP的第i行的所有元素的初始矩陣行又可以組成1 個一維矩陣(元素的初始矩陣行等于該元素整除矩陣維數的商)，定義為水平行陣h，數據結構如圖3所示：

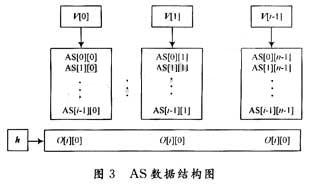
　定義：垂直沖突值：vRepeat[n]，其中vRepeat[i](i=0，1，2，…，n-1)等于u[i]中的元素在h中的重復次數的和。

　　水平沖突值：hRepeat[n]，其中hRepcat[i](i=0，1，…，n-1)等于k[i]在v中的重復次數的和。

　　生存數(lifenum)：假設vRepeat[j]等于k，也就是說，O[i]中有k個元素不能放在AS的第j列，能放在這一列的元素個數只有n-k個，定義為生存數(lifenum)，將這n-k個元素下標取出形成向量，定義為生存空間(lifespace)

　　5.2 高沖突值行優先排列算法的實現

　　算法安放數據元素時，首先從vRepeat最大的那一列開始安放hRepeat最大的符合“規則”的元素，再逐次安放vRepeat中較小的且符合“規則”的列。這樣，大沖突值的元素得到優先安放，重排或回溯的可能性就大大減小。

　　5.2.1 主流程

　　(1)排列第1行數據，row=0；

　　(2)row=row+1，如果row≥n，則停止，否則轉下一步；

　　(3)統計沖突值，調用判回溯算法判斷是否回溯，如果回溯，調用回溯算法，否則轉下一步；

　　(4)選擇vRepeat沖突值最大的列，根據“規則”安放hRepeat中最大的元素；

　　(5)更新vRepeat和hRepeat；

　　(6)判斷這一行的數據是否都安放完畢，如果是，轉(2)，否則轉(3)。

　　5.2.2 判斷回溯算法

　　回溯條件：生存數為k，生存空間相同的列的個數和大于生存數k，則回溯，原因是某生存空間“不夠分配”。例如，第i列和第j列(i不等于j)的生存數都為1和生存空間都為{2}，這樣第2個元素只能放在一個位置上，也就是說，無論如何排列都無法滿足“規則”，需要回溯。

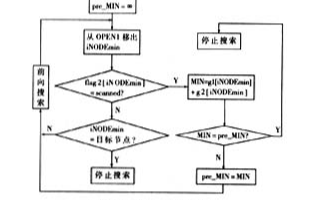
　　定義節點數據結構如圖4所示：

　　判回溯的算法流程：

　　(1)將生存數相同的所有節點串成鏈表，鏈表的序號等于生存數；

　　(2)從鏈表序號為0向鏈表序號為n順序掃描鏈表，統計生存空間相同的節點個數，當出現節點個數大于生存數的情況，需要回溯，否則轉下一步；

　　(3)將本鏈并入下一個鏈表；

　　(4)如果所有鏈表都不出現生存空間相同的節點個數和大于生存數的情況，則不需要回溯。

　　5.2.3 回溯算法

　　定義經歷表：在回溯過程中，各元素所“呆過”的位置序列。

　　回溯算法流程：

　　(1)確定回溯元素(沖突值最大原則)；

　　(2)為回溯元素找一個“合法位置”；

　　合法條件：

　　規則：沖突值小于當前情況；位置不在經歷表中。

　　(3)為其他元素找“合法位置”；

　　6 算法的正確性證明和復雜度分析

　　從前面的分析可以知道，要解決整個交換算法的關鍵是確定和尋找中間矩陣after_s，也就是說，在解決問題之前，必須確定問題有解。如何確定after_s一定存在，這里可以通過組合數學中的抽屜原理證明必然存在這樣的矩陣，證明過程比較簡單，本文在這里不做推導證明。

　　從前面的理論分析中知道，衡量交換算法有2個重要的指標：交換次數和比較次數。為了統計本文所研究的交換算法的性能，本文針對不同階數矩陣的交換次數和比較次數做了系統的統計：

　　(1)對于每一行數據，由于統計沖突值、判回溯算法和元素的安放算法都是多項式復雜度，所以，在不存在回溯的條件下，本算法是多項式復雜度。

　　(2)在本算法中，“沖突”起著非常重要的作用，本身回避了許多回溯可能。即使回溯，本行可供回溯元素和非回溯元素“待”的位置個數非常有限，所以元素回溯的空間很小。

　　下面本文給出在不回溯的情況下，對高沖突行優先排列算法在階數遞增變化時，50次平均交換次數和比較次數統計結果如表1所示。

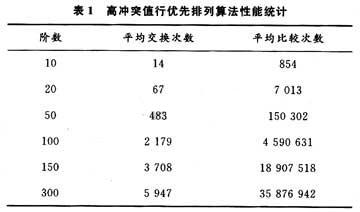
　　從前面對該算法的描述可知，該算法通過使每個元素“找到”盡可能適合自己的位置，從而回避了重新排列的許多可能，對于一行來說，完全避免了全排列，而且大大減小回溯概率。由于對大多數(約80％)矩陣來說，是不會出現回溯的，只有類似這樣的矩陣才有可能出現回溯(也可能不回溯)，即，AS的某些行，可供選擇的初始行太少。所以，該算法是一個近似多項式的算法，在不回溯的情況下，是多項式算法。該算法基本上能夠完成交換網絡的路徑接續，他有一個很大的優勢就是在交換過程中交換的次數達到最小，這樣也就大大提高了尋找交換路徑的效率。本算法具有良好的特性，而且通過芯片級聯可實現。