三電容電路時(shí)域分析

然后，我們從時(shí)域的角度把三電容電路的機(jī)理再過(guò)一次（非常重要！是深入理解三電容電路并幫你通過(guò)面試拿到offer的關(guān)鍵！）。

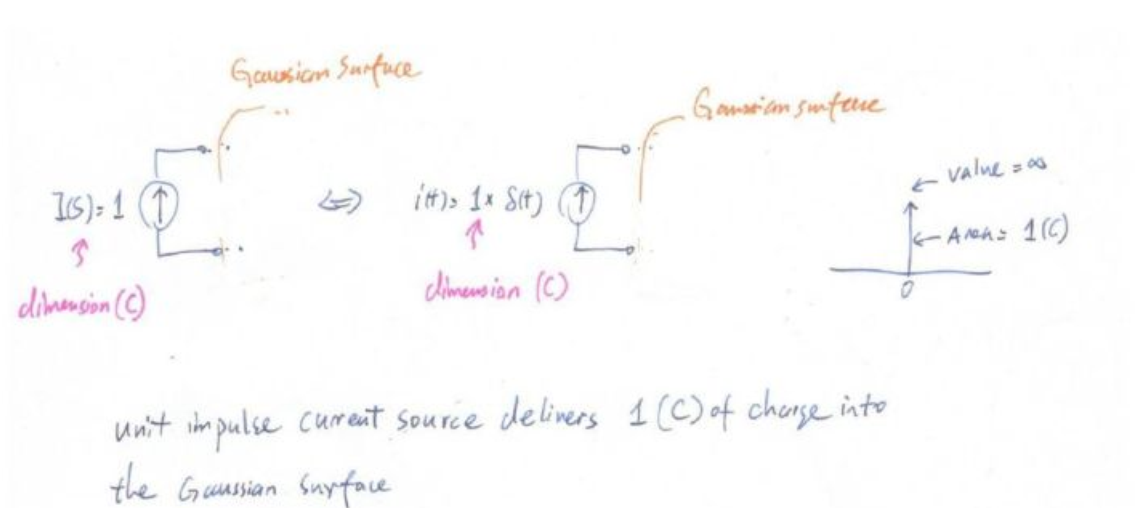
我們必須要先理解沖激電流的物理意義。單位沖激電流在拉普拉斯域的表示為1。注意這個(gè)1是有單位的，單位是庫(kù)倫，大家可以思考一下為什么電流的拉普拉斯轉(zhuǎn)換的單位是庫(kù)倫。在時(shí)域里，單位沖激函數(shù)前面的1的單位也是庫(kù)倫，因?yàn)閱挝粵_激函數(shù)的積分為1，但是電流的積分必須是庫(kù)倫，所以這里的1代表了一個(gè)包裹的1庫(kù)倫電荷，這個(gè)1庫(kù)倫的電荷只需要0時(shí)間就可以被輸送，因?yàn)樵趖=0的時(shí)候，電流無(wú)窮大。

所以，單位沖激電流的物理意義就是用0時(shí)間通過(guò)無(wú)窮大的電流向一個(gè)高斯面里輸送了1庫(kù)倫電荷。

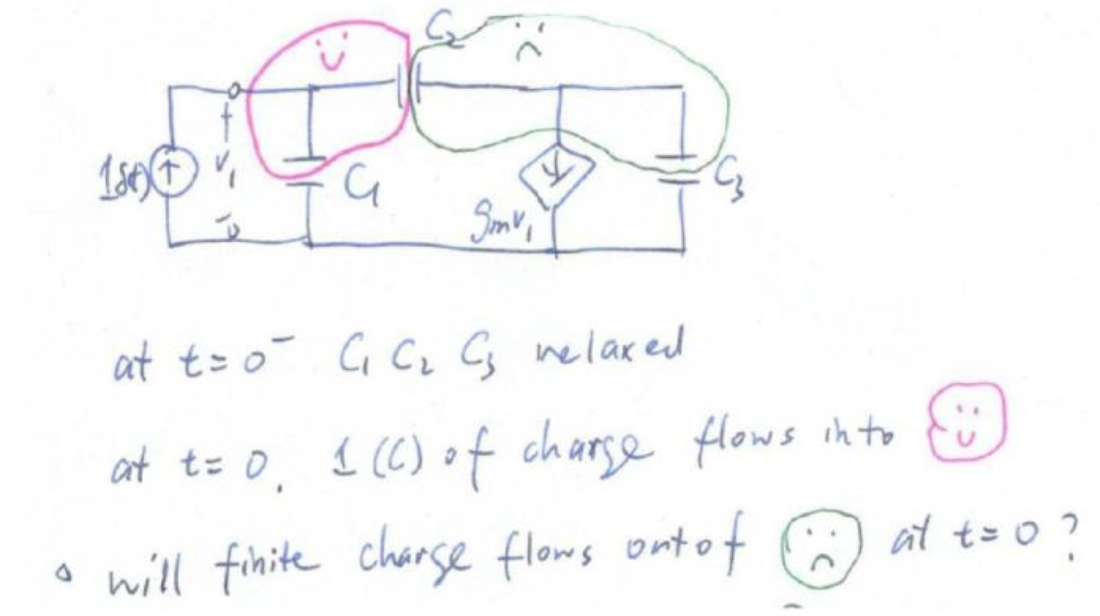
現(xiàn)在回到三電容電路，在t=0-時(shí)，三個(gè)電容都沒(méi)有初始電荷。在t=0時(shí)，1庫(kù)倫的電荷被注入到了紅色高斯面里。現(xiàn)在的問(wèn)題是，會(huì)不會(huì)有有限量的電荷在t=0時(shí)流入綠色高斯面。我們來(lái)分析這個(gè)情況：

如果有有限量的電荷流入綠色高斯面，那說(shuō)明受控源gmv1必須是無(wú)窮大，因?yàn)闊o(wú)窮大的電流才能在0時(shí)間內(nèi)輸送有限的電荷，有限的電流在0時(shí)間內(nèi)輸送0電荷。

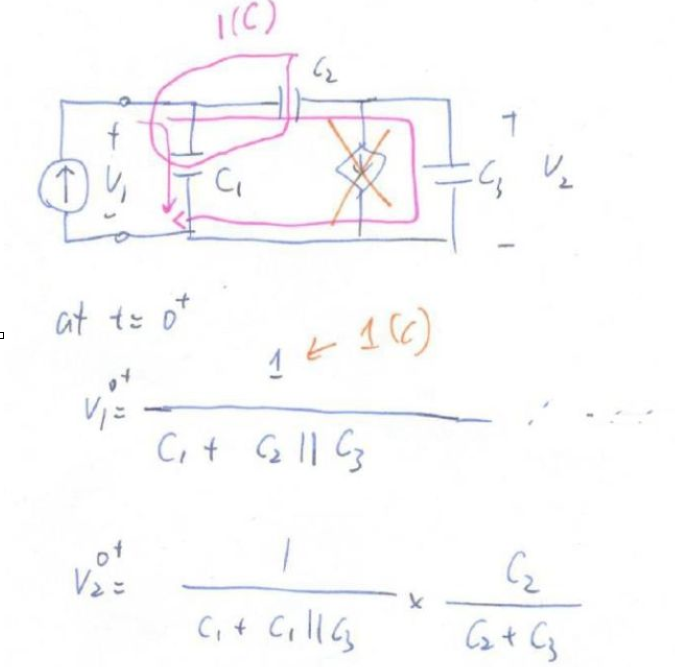
這表示v1是無(wú)窮大，但是v1無(wú)窮大的話，紅色高斯面內(nèi)必須有無(wú)窮大的電荷，這不可能，因?yàn)闆_激電流所攜帶的電荷是有限的。所以受控源電流是有限的，受控源在0時(shí)間內(nèi)不輸送任何電荷。所以在t=0+時(shí)，只有電荷會(huì)在C1 C2 C3 中重新分布，1庫(kù)倫的電荷會(huì)在C1+C2||C3這個(gè)總電容上建立一個(gè)電壓v1（0+）。C2 和C3必須形成一個(gè)分壓器，因?yàn)镃2的右極板和C3的上極板的電荷總和為0。這樣我們可以推出v2（0+）：

化簡(jiǎn)v2（o+），我們可以得到：

這跟我們之前用拉普拉斯轉(zhuǎn)換得到的結(jié)果一致！

下面看最終狀態(tài)，當(dāng)電路達(dá)到最終狀態(tài)時(shí)，所有的狀態(tài)變量都不再改變了（除非我們有共振或者不穩(wěn)定的特殊情況，然而這個(gè)電路顯然沒(méi)有），這說(shuō)明受控源gmv1必須為0，v1必須為0。但是當(dāng)t》0時(shí)，紅色高斯面內(nèi)的電荷就不再會(huì)改變了，因?yàn)楠?dú)立電流源為0，所以所有1庫(kù)倫的電荷都必須被“擠壓”到C2上，產(chǎn)生電壓1/C2。因?yàn)関1（∞）為0，所以我們可以算出v2（∞）為-1/C2。

這又跟我們用拉普拉斯轉(zhuǎn)換得到的結(jié)果一致！

我們之已經(jīng)分析過(guò)，這個(gè)電路只有一個(gè)非無(wú)窮大的時(shí)間常量，所以這是一個(gè)“準(zhǔn)一階電路”。對(duì)于這種電路，只要我們知道在t=0+的初始值和t=∞的終值，中間的行為就是一個(gè)一階指數(shù)衰減。所以我們得到與之前一致的響應(yīng)：