極點零點對消與極點分裂法(見前述推文)一樣，可以使兩個極點分離
2023-10-18 15:09:55
92 
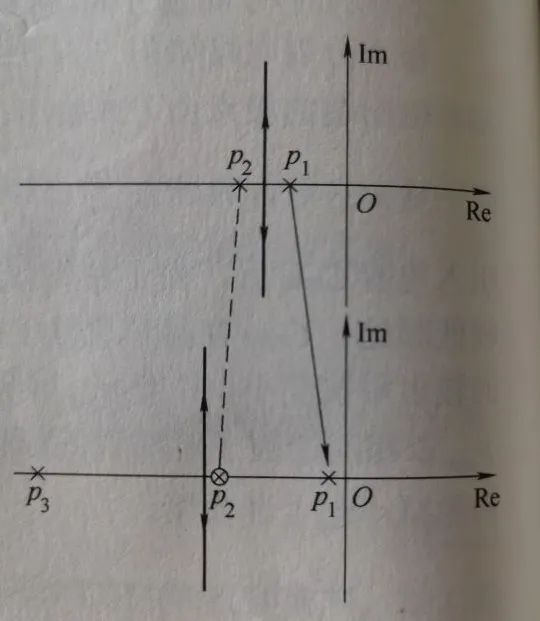
根軌跡分析法是通用分析方法，不是具體的補償操作方法，下面介紹的極點分裂法是一種具體的電路操作方法
2023-10-18 14:56:3471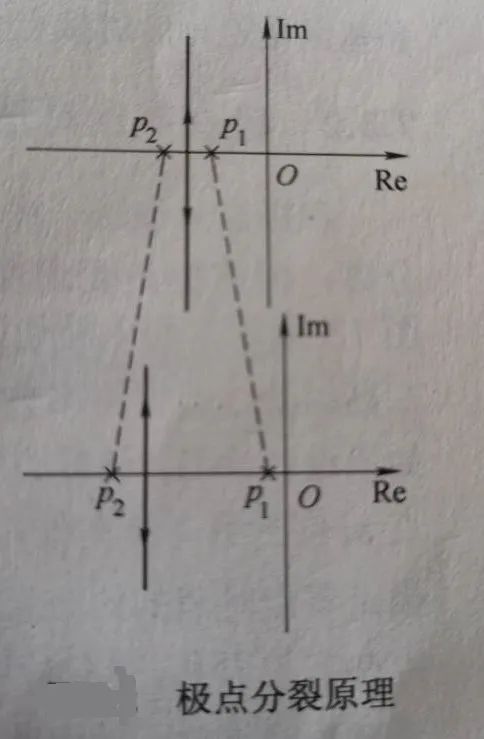 
為什么頻率最小的極點稱為主極點？? 極點是控制系統穩定性的重要因素，而頻率最小的極點被稱為主極點，因為它對系統的穩定性起著最主要的作用。在控制系統中，極點是指對系統輸出有決定性影響的最小階段差的復
2023-09-20 16:43:30118 微分方程的求解；（4） 熟練掌握一階電路的三要素法，會分析計算一階電路的階躍響應；（5） 掌握二階電路的微分方程、特征方程的建立和電路固有頻率的概念；（6） 熟練掌握RLC串聯電路和并聯電路的零輸入響應
2008-11-25 15:12:37
這一篇文章我們主要看下OP閉環電路小信號分析中常見的問題。有時候我們發現stb分析（β=1）的bode圖和開環AC仿真的曲線相差很大，且兩者的零極點位置、裕度等可能大有不同。探究造成該問題的原因，很有可能是我們在AC開環分析時沒有計入反饋元件和輸入級寄生電容的影響。
2023-07-14 16:15:49206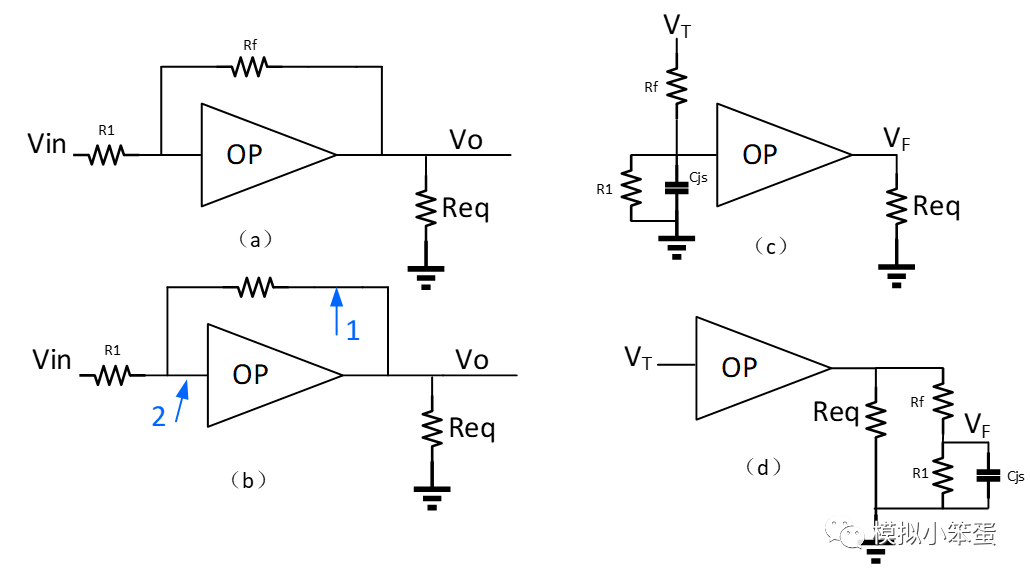 
被控對象不穩定極點是指具有正實部的極點，它們所對應的模態隨著時間的推移而發散，導致系統變得不穩定。
2023-06-30 16:59:54619 
在信號處理和系統理論領域，零極點分析是一項重要的技術，用于研究和分析濾波器的特性和行為。
2023-06-20 16:35:032556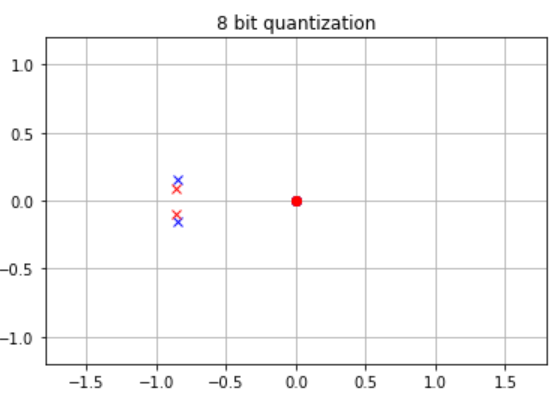 
Zi是分子多項式零點，稱為傳遞函數零點，Pj是分母多項式零點，稱為傳遞函數極點。系數K*=b0/a0稱為傳遞函數系數或根軌跡增益。
2023-03-09 16:51:458169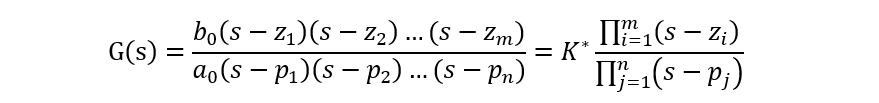 
晶體濾波器的四極點（Fourier poles）是指在頻域中，晶體濾波器傳遞函數的極點。在濾波器中，傳遞函數是指輸入和輸出之間的關系，它通常可以用復數形式表示。在頻域中，復數傳遞函數可以看作是極點和零點的乘積。
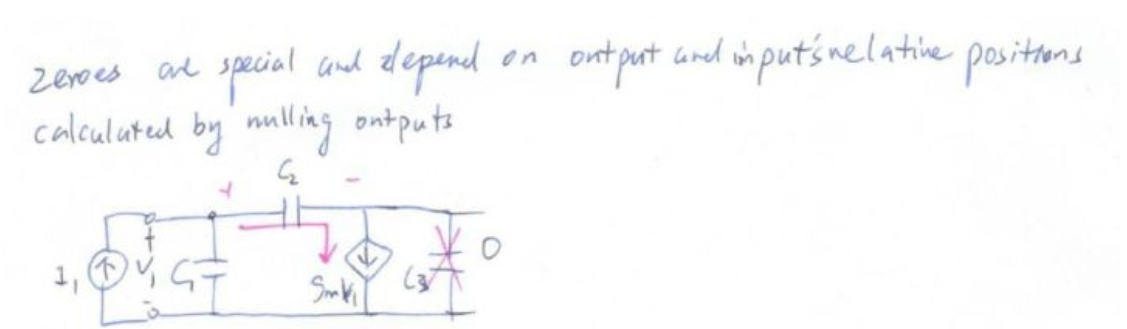
2023-02-27 11:39:49323 不知不覺，環路內容已經寫了7節了，以理論分析為主，下面來說說兄弟們都很關心的內容——零點和極點。
2023-02-16 09:30:132313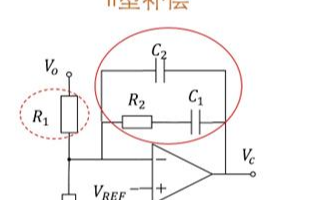 
高速PCB設計指南之三
2022-12-30 09:22:13
0 假如R=1Khz，C=1uF，那么極點是s=-1000，但是我們通常說極點是1000，理由貌似是自然界中沒有負頻率，所以對s求了個模，頻率w=|s|=1000，我們把這個求模后的值也還是叫極點，并沒有重新取名字。
2022-05-30 10:46:0210249 Multisim仿真之三極管資料免費下載。
2022-04-08 14:45:0016 在這里，作者將嘗試找出關于極點和零點的物理感覺，使用運算放大器來控制它們在復平面中的位置，并利用電路的自然響應來說明極點/零點位置的影響。
2022-02-17 16:26:5620475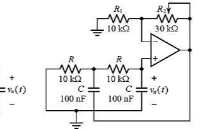 
電容影響形成了一個不想要的極點。引入輸入電容來計算反饋網絡的阻抗特性是保證運放電路穩定性的重要一步。但是，哪種電容有影響？差模電容？共模電容？還是都有？ 運放輸入電容一般可以在輸入阻抗參數一欄找到，差模電容和
2021-11-19 15:33:272248 電子發燒友網站提供（電源反饋設計速成篇之三仿真篇）資料免費下載。
2020-11-11 11:37:2717 分析，蒙特卡羅分析，批處理分析，用戶自定義分析，噪聲系數分析。 1.直流工作點分析（DC Operating）：在進行直流工作點分析時，電路中的交流源將被置零，電容開路，電感短路。 2.交流分析（AC Analysis）：交流分析用于分析電路的頻率特性。
2020-11-10 10:55:437516 在這篇文章中，我將嘗試找出關于極點和零點的物理感覺，使用運算放大器來控制它們在復平面中的位置，并利用電路的自然響應來說明極點/零點位置的影響。
2020-09-27 13:07:191837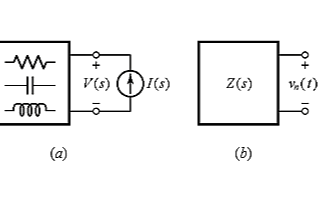 
白板演示系列: ADI Matt Duff講解使用電阻電容的單極點濾波器配置。
2019-07-08 06:17:002256 1.2 開關模式電源轉換器補償簡單易行 零點和極點
2019-04-12 06:38:004433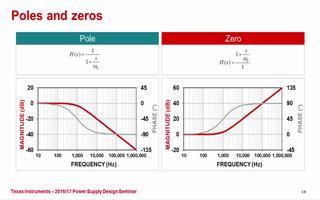 
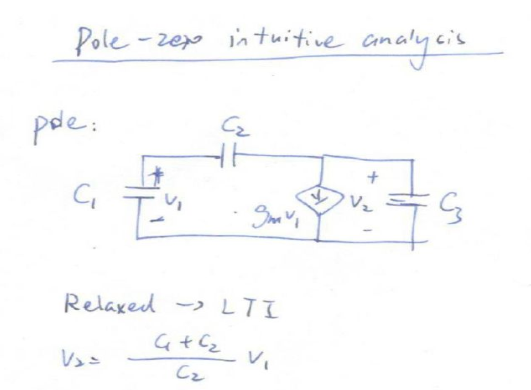
將嘗試找出關于極點和零點的物理感覺，使用運算放大器來控制它們在復平面中的位置，并利用電路的自然響應來說明極點/零點位置的影響。 單端口電路的自然響應 我們來看圖1中的無源線性單端口電路，它包括電阻、電容和電感
2019-01-04 16:21:01628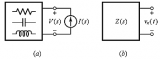 
零極點補償器(Pole-zero compensator)常用于修正反饋放大器回路的幅度和相位。這篇文章超出了教科書標準的解釋程度，本文考慮了工程師在使用補償器設計電路時需要注意的地方，甚至還涉及了補償器設計所采用晶體管的細節。
2018-06-05 09:54:0013312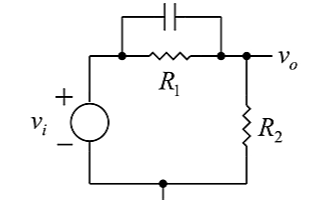 
零點：當系統輸入幅度不為零且輸入頻率使系統輸出為零時，此輸入頻率值即為零點。極點：當系統輸入幅度不為零且輸入頻率使系統輸出為無窮大（系統穩定破壞，發生振蕩）時，此頻率值即為極點。下面就來談談兩者的區別。
2018-03-19 16:52:0090991 零極點的理解是模擬電路最關鍵的基礎之一，信號與系統都會講自然響應，自然響應就是偏微分方程的通解部分，而受迫響應則是偏微分方程的特解。本文將詳解零極點與頻率響應之間的關系。
2018-02-21 10:26:0045632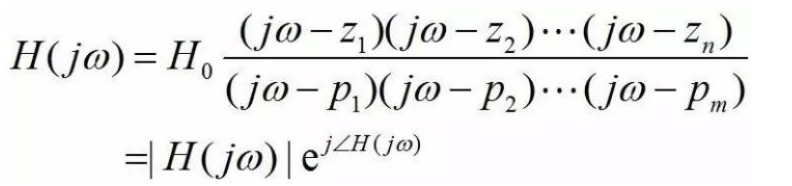 
其實電路的每個node都有一個極點，但是他到底長啥樣？只要輸入和輸出之間有兩條通路就會產生一個零點，零點并不能單單的說是由于前饋，反饋，或者串聯并聯一個電容產生的。產生的原因還是和具體的電路結構相關聯的。
2018-02-21 09:19:008610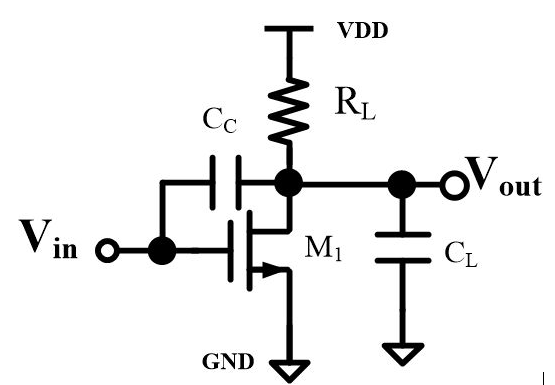 
極點的定義是輸出變為無窮大，極點的存在會給電路的不同頻率的小信號帶來不同的反應，唯一的極點就在輸出Vout，輸出阻抗Rout等于上面那個resistor和下面的ro并聯，當小信號的頻率變得非常大之后，系統對極高頻率的信號也就無限衰減了。
2018-02-21 08:06:002352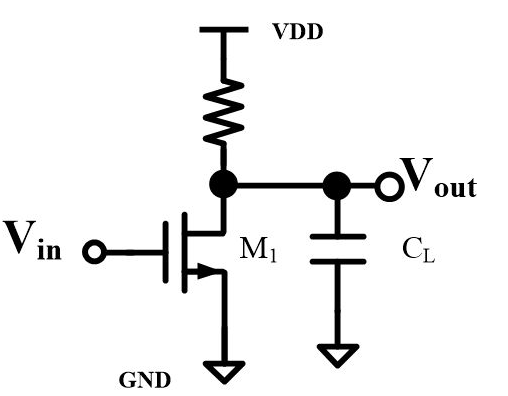 
Orcad中對三極管放大電路的仿真，瞬態、電容Ce變化下的分析
2017-04-24 15:12:059 電路教程相關知識的資料，關于電路中極點與零點的產生與影響
2016-10-10 14:17:5930 雙極點_雙零點控制器在Boost電路中的實現_龔雄，感興趣的小伙伴們可以看一看。
2016-09-12 16:55:386 Labview之動態窗口樣式之三，很好的Labview資料，快來下載學習吧。
2016-04-19 10:56:2234 Labview之上機實驗之三，很好的Labview資料，快來下載學習吧。
2016-04-19 10:23:1632 Proteus之矩陣式鍵盤的識別之三，很好的Proteus資料，快來下載不學習吧。
2016-04-18 16:42:3223 從零開始MQX開發之三添加新的開發板到CodeWarrior項目向導
2015-11-26 14:52:1520 電路如果存在不穩定性因素，就有可能出現振蕩。本文對比分析了傳統LDO和無片電容LDO的零極點，運用電流緩沖器頻率補償設計了一款無片外電容LDO，電流緩沖器頻率補償不僅可減小片
2013-09-03 17:07:3230 高速PCB設計指南之三
第一篇 改進電路設計規程提高可測試性
隨著微型化程度不斷提高，
2009-11-11 15:01:16469
有衰減極點的低通濾波器電路圖
2009-07-16 17:18:06655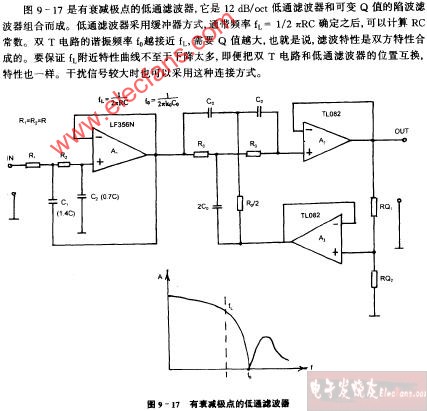 
網絡函數教案(ppt講稿):1、網絡函數及其相關的基本概念。2、網絡函數的零、極點分布對時域響應和頻域響應（頻率特性）的影響。網絡函數的零、極點分布對頻域響應（頻率
2009-07-08 10:23:3823
有兩個可變零點、兩個固定極點的有源濾波器
2009-04-15 10:51:17462 
五極點有源濾波器電路圖
2009-03-30 09:36:33534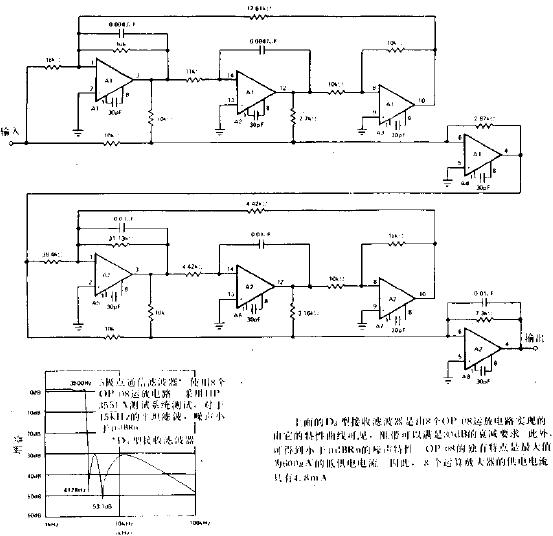 
雙極點低通布特沃思濾波器電路
2008-06-11 10:20:071654 數位電容表原理分析及電路圖
2007-11-16 23:52:2272 CAM350 技巧之三1. 問：cam350 是如何獲得鉆孔信息的，如果藍圖里面沒有標示，cam350 能讀出孔嗎？答：在Import Drill date 直接讀出鉆孔文件層就
2007-01-25 12:05:023088
正在加载...
電子發燒友App
工商網監
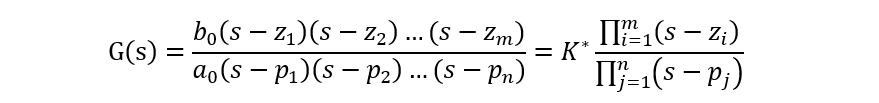
評論