經典手算法設計二級運放
手算法其實就是根據設計要求,把結構定下來之后運用運放的一些基礎知識將MOS管的W/L參數一一定下來的方法,這個方法不一定能設計出很完美的運放,但是對運放的深入理解是很有幫助的。
二級運放涉及參數——這些參數決定著一個運放的優劣,但更重要的是根據不同的場合來選擇合適的運放(參數定義有不清楚的請自行翻書):
1、增益
增益
2、單位增益帶寬(GB)
單位增益帶寬
3、沉降時間
穩定時間
4、壓擺率
擺率
5、輸入共模范圍
共模輸入范圍
6、共模抑制比
共模抑制比
7、電源抑制比
電源抑制比
8、輸出電壓擺幅
輸出擺率
9、輸出電阻
輸出阻抗
10、膠印
失調電壓
11、噪音
噪聲
12、布局區域
版圖面積
上述參數只涉及運放設計的一部分要求,而對運放來說,穩定性是其最基礎而又最重要的要求。 上述參數并未涉及到穩定性相關參數,下面對典型二級運放的穩定性進行一些基礎分析。
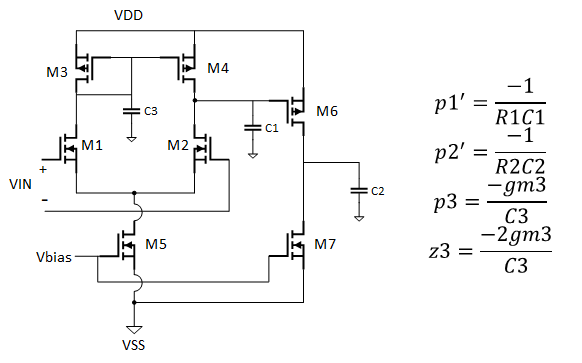
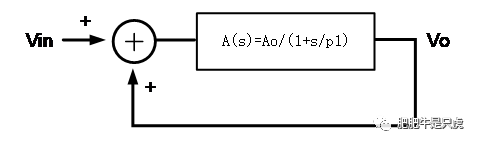
上圖為沒有進行補償的二級運放示意圖,其中C1、C3為寄生電容,C2為寄生電容+負載電容。
因此圖中主要存在3個極點和1個零點,分別羅列在上圖右側,其中p3與z3分別為鏡像極點與鏡像零點(為啥叫鏡像? 估計因為是電流鏡M3、M4柵極節點上的?),且通常p3、z3遠大于GB,對運放的穩定性影響很小; p3、z3相距較近,趨向相互抵消。 剩下的p1’、p2‘兩個主次極點由于相距相對較近,頻率也不大,因此對運放的穩定性影響較大。
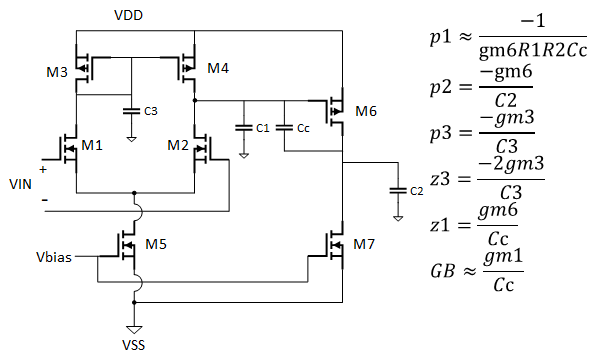
上圖為補償后的二級運放示意圖,其中Cc為米勒補償電容。
同圖1,p3、z3對運放的穩定性影響很小,但其主次極點發生了變化,實現了極點分裂,分別為上圖右側的p1與p2,極點的分裂給運放的穩定性帶來了正面的效果。 在該二級運放中,還引入了右半平面的零點z1,這可能會給穩定性帶來影響。
上述公式中,GB=|p1|×GAIN≈gm1/Cc。
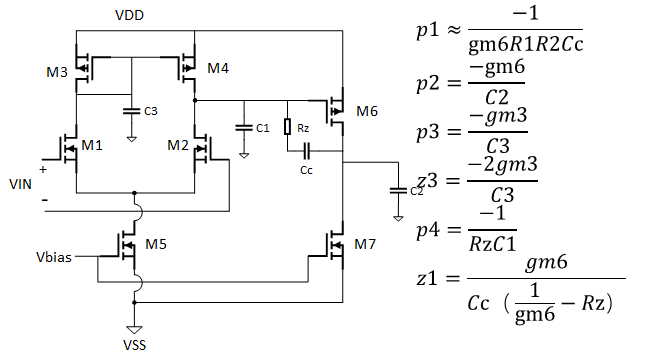
上圖為帶調零電阻的補償后的二級運放示意圖,其中Rz為調零電阻,Rz可以使運放更加穩定。
由圖2可知,零點z1會給運放的穩定性帶來影響,而Rz的出現,使零點z1發生了改變。 此時只需調整Rz的大小,使1/gm6-Rz=0,零點z1就可以移動至無窮大; 也可以將其從右半平面移動到左半平面并與p2抵消。 在實際設計時,我們也可以采用上述方法利用Rz來減小對運放穩定性影響的,如通過仿真得到gm6的值,再取其倒數估算Rz的大小。
前面給出了同一結構的運放在不同補償條件下的零極點,下面就來總結一下什么樣的零極點對運放來說才是穩定的。
說到零極點與穩定性,就能聯想到波特圖,下面就結合波特圖直接從結論推出我們想要的結論:
1、在波特圖中,每個零點頻率處,幅值曲線的斜率按+20dB/dec變化,每個極點頻率處,幅值曲線的斜率按-20dB/dec變化。
2、對一個ωm的極點(零點)頻率,相位約在0.1ωm的地方開始下降(上升),在ωm處經歷-45°(+45°)的變化,在大約10ωm處達到-90°(+90°)的變化。
3、高頻極點和零點對相位的影響可能比對幅值的影響更大。
4、在穩定系統中,增益交點(GX)必定發生在相位交點(PX)之前,增益交點指的是環路增益的幅值等于1
的頻率,相位交點指的是環路增益的相位等于-180°的頻率。 GX對應頻率與單位增益帶寬相同。
5、GX與PX的間距越大,反饋系統越穩定。
6、相位裕度(PM)=180°+∠βH(ω=ω1),其中ω1是GX頻率。 當PM≥60°,系統被認為是穩定的。
由1~6可知:
1、對于一個單極點系統是無條件穩定的,因為單個極點不可能產生大于90°的相移。
2、對于一個雙極點系統,當GX對應的頻率正好是第二極點時,可以證明此時的PM=45°。 因此為確保PM≥60°,第二極點必須出現在GX頻率之后(約2.2~3倍GB處)。
3、對于除了主次極點外其他會影響穩定性的零極點,我們希望其頻率>10GB。
下面就根據以上分析,正式進入今天的主題:設計一個滿足要求的二級運放。
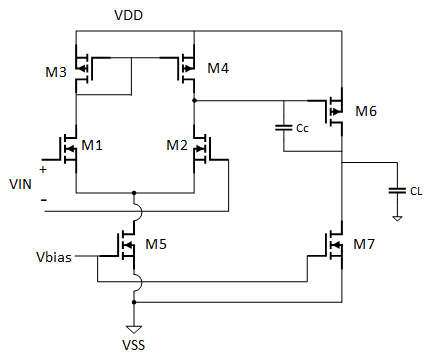
設計案例
設計如上圖所示的二級運放,條件如下:
Av>3000V/V,VDD=5V,VSS=0V,GB=5MHz,SR>10V/us,PM=60°,ICMR=1.5~4.5V,
輸出電壓范圍=0.5~4.5V,功率≤2mW,CL=10pF
設計步驟:
①首先選擇合適的工藝,假設該工藝kn=110uA/V2,kp=50uA/V2,VTN=0.55V,VTP=0.85V.
②由60°PM可知:|p2|>2.2GB且|z1|>10GB,因此gm6/CL>2.2gm1/Cc且gm6/Cc>10gm1/Cc,因此gm6>10gm1→1/CL>0.22/Cc→Cc>0.22CL=2.2pF,這里取Cc=3pF。
(3)∵SR=Id5/Cc>10V/us→
Id5>10V/us×3pF=30uA,取I5=30uA。
(4)∵GB=gm1/Cc=5MHz→gm1=15*2π=94.2uS
∵gm=√(2kn *W/L *I) →W/L=2.69≈3
于是可以得到M1、M2管的寬長,取W/L=6um/2um。
⑤∵ICMR_max=4.5V→Vov3_min=VDD-(ICMR_max-VTN)-VTP=5-(4.5-0.55)-0.85=0.2V,若此時M3仍飽和,則滿足平方律公式,且Id3=15uA,由此可推出M3、M4的寬長比W/L=2Id/(kp*Vov2)=15,
取W/L=30um/2um。
⑥∵ICMR_min=1.5V→若要確保M5進入飽和狀態,Vov5_min=Vds5=ICMR_min-(Vov1+VTN)=1.5-(√(2I/(kn*W/L))+0.55)=0.65V,且Id5=30uA,由此可推出M5的寬長比W/L=2Id/(kp*Vov2)=1.29≈1.5,取W/L=3um/2um。
⑦∵gm6>10gm1,取gm6=942uS。 由于穩態時VGS4=VGS6,且gm=k*W/L*Vov,因此gm6/gm4=(W/L)6/(W/L)4→(W/L)6=gm6/gm4*(W/L)4=942uS/√(2kp *(W/L)4*Id4)*15=94.2,取W/L=188um/2um。
⑧由gm=√(2k *W/L*I)→Id6=94.4uA,因此可得到M7的寬長比(W/L)7=(W/L)5*94.4/30=4.7,取W/L=10um/2um。
⑨∵Vov=2Id/gm=√(2Id/(k*W/L)),∴Vov6=0.2V,Vov7=0.58V,由此可得輸出電壓最大值為5-0.2=4.8V>4.5V,而最小輸出電壓為0.58V>0.5V,不符合最小輸出電壓范圍,此時可選擇適當增大M7管的寬長比。
(10)Av=gm1/(Id5/2*(l2+λ4))gm6/(Id6(λ6+λ7))=7736>3000V/V,因此增益符合要求。
Pdiss=5V*(30+94.4)uA=0.62mW<2mW,因此功耗也符合要求。
以上是對典型二級運放的一個粗略的設計,最后可以將計算出的運放尺寸代入仿真模型,通過電路仿真來驗證其是否滿設計要求,并做最后的優化。 在實際設計過程中不難發現,一些與工藝相關的參數是不容易找到的,最終還是要通過代入工藝模型來進行多次的仿真調整,才能得到比較可靠的結果。
 電子發燒友App
電子發燒友App












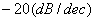











評論