電化學(xué)交流阻抗譜圖
? ? ? 交流阻抗發(fā)式電化學(xué)測(cè)試技術(shù)中一類十分重要的方法,是研究電極過(guò)程動(dòng)力學(xué)和表面現(xiàn)象的重要手段。特別是近年來(lái),由于頻率響應(yīng)分析儀的快速發(fā)展,交流阻抗的測(cè)試精度越來(lái)越高,超低頻信號(hào)阻抗譜也具有良好的重現(xiàn)性,再加上計(jì)算機(jī)技術(shù)的進(jìn)步,對(duì)阻抗譜解析的自動(dòng)化程度越來(lái)越高,這就使我們能更好的理解電極表面雙電層結(jié)構(gòu),活化鈍化膜轉(zhuǎn)換,孔蝕的誘發(fā)、發(fā)展、終止以及活性物質(zhì)的吸脫附過(guò)程。
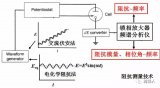
交流阻抗譜檢測(cè)方法是給被測(cè)體系施加一個(gè)小振幅的單正弦波擾動(dòng),或者是不同頻率正弦波的疊加,一般是正弦波形式的電壓或者是電流,結(jié)果產(chǎn)生相應(yīng)的電流或電壓的響應(yīng)信號(hào)。
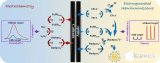
如圖2上圖電流電壓曲線所示,在體系直流電壓E。的條件下外加正弦波電壓Esin(ωt)(ω為角頻率),那么在直流電流I0的基礎(chǔ)上就會(huì)得到一個(gè)正弦波電流I=sin(ωt+Ф)。得到的電流響應(yīng)值I受外加電壓E控制。根據(jù)歐姆定律Z(ω)=E(ω)/I(ω)可計(jì)算出在某個(gè)頻率下體系的阻抗值z(mì)。

在電化學(xué)阻抗技術(shù)中,z被定義為一個(gè)復(fù)數(shù),即Z(ω)=Zre(ω)+jZim(ω),Z2=Zre2+Zim2。其中實(shí)部 Zre=∣ Z∣cosθ,虛部Zim=∣Z∣Sinθ相位角θ=tan-1(Zim/Zre)。
以Zre對(duì)Zim作圖,稱為Nyquist圖譜(如圖2下圖左圖譜所示),可以清晰地給出實(shí)部和虛部的數(shù)值,并可進(jìn)行體系定性分析。但它不能給出頻率信息,所以通常要采用其它曲線來(lái)補(bǔ)充。
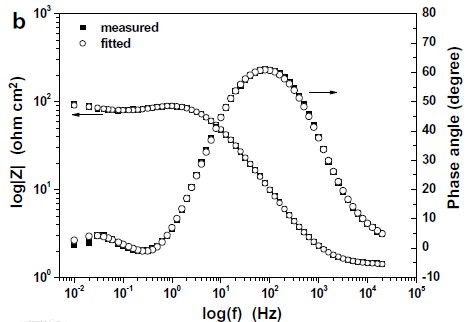
另外一種常用的表示方法是Bode圖,即lgZ、相角對(duì)頻率作圖(如圖2下圖右圖譜所示),圖譜中同時(shí)表示了阻抗與頻率、相移與頻率的關(guān)系。
一般Nyquist圖譜比較普遍,Nyquist圖譜是由一個(gè)半圓部分和一個(gè)線性部分組成,半圓部分在高頻區(qū),對(duì)應(yīng)的是電子轉(zhuǎn)移限制過(guò)程,半圓越大,電阻就越大,后面直線部分在低頻范圍,對(duì)應(yīng)的是擴(kuò)散限制過(guò)程。
1、阻抗譜中的基本元件
交流阻抗譜的解析一般是通過(guò)等效電路來(lái)進(jìn)行的,其中基本的元件包括:純電阻R,純電容C,阻抗值為1/jωC,純電感L,其阻抗值為jωL。實(shí)際測(cè)量中,將某一頻率為ω的微擾正弦波信號(hào)施加到電解池,這是可把雙電層看成一個(gè)電容,把電極本身、溶液及電極反應(yīng)所引起的阻力均視為電阻,則等效電路如圖1所示。
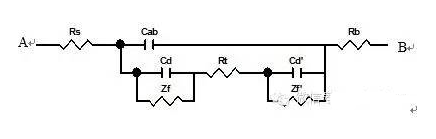
圖1.用大面積惰性電極為輔助電極時(shí)電解池的等效電路
圖中A、B分別表示電解池的研究電極和輔助電極兩端,Ra、Rb分別表示電極材料本身的電阻,Cab表示研究電極與輔助電極之間的電容,Cd與Cd’表示研究電極和輔助電極的雙電層電容,Zf與Zf’表示研究電極與輔助電極的交流阻抗。通常稱為電解阻抗或法拉第阻抗,其數(shù)值決定于電極動(dòng)力學(xué)參數(shù)及測(cè)量信號(hào)的頻率,Rl表示輔助電極與工作電極之間的溶液電阻。一般將雙電層電容Cd與法拉第阻抗的并聯(lián)稱為界面阻抗Z。
實(shí)際測(cè)量中,電極本身的內(nèi)阻很小,且輔助電極與工作電極之間的距離較大,故電容Cab一般遠(yuǎn)遠(yuǎn)小于雙電層電容Cd。如果輔助電極上不發(fā)生電化學(xué)反映,即Zf’特別大,又使輔助電極的面積遠(yuǎn)大于研究電極的面積(例如用大的鉑黑電極),則Cd’很大,其容抗Xcd’比串聯(lián)電路中的其他元件小得多,因此輔助電極的界面阻抗可忽略,于是圖1可簡(jiǎn)化成圖2,這也是比較常見(jiàn)的等效電路。
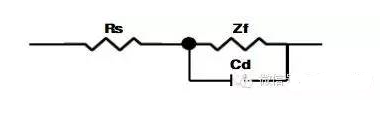
圖2.用大面積惰性電極為輔助電極時(shí)電解池的簡(jiǎn)化電路
2、阻抗譜中的特殊元件
以上所講的等效電路僅僅為基本電路,實(shí)際上,由于電極表面的彌散效應(yīng)的存在,所測(cè)得的雙電層電容不是一個(gè)常數(shù),而是隨交流信號(hào)的頻率和幅值而發(fā)生改變的,一般來(lái)講,彌散效應(yīng)主要與電極表面電流分布有關(guān),在腐蝕電位附近,電極表面上陰、陽(yáng)極電流并存,當(dāng)介質(zhì)中存在緩蝕劑時(shí),電極表面就會(huì)為緩蝕劑層所覆蓋,此時(shí),鐵離子只能在局部區(qū)域穿透緩蝕劑層形成陽(yáng)極電流,這樣就導(dǎo)致電流分布極度不均勻,彌散效應(yīng)系數(shù)較低。表現(xiàn)為容抗弧變“癟”,如圖3所示。另外電極表面的粗糙度也能影響彌散效應(yīng)系數(shù)變化,一般電極表面越粗糙,彌散效應(yīng)系數(shù)越低。
2.1、常相位角元件(ConstantPhaseAngleElement,CPE)
在表征彌散效應(yīng)時(shí),近來(lái)提出了一種新的電化學(xué)元件CPE,CPE的等效電路解析式為:

角為φ=--pπ/2,由于它的阻抗的數(shù)值是角頻率ω的函數(shù),而它的幅角與頻率無(wú)關(guān),故文獻(xiàn)上把這種元件稱為常相位角元件。
實(shí)際上,當(dāng)p=1時(shí),如果令T=C,則有Z=1/(jωC),此時(shí)CPE相當(dāng)于一個(gè)純電容,波特圖上為一正半圓,相應(yīng)電流的相位超過(guò)電位正好90度,當(dāng)p=-1時(shí),如果令T=1/L,則有Z=jωL,此時(shí)CPE相當(dāng)于一個(gè)純電感,波特圖上為一反置的正半圓,相應(yīng)電流的相位落后電位正好90度;當(dāng)p=0時(shí),如果令T=1/R,則Z=R,此時(shí)CPE完全是一個(gè)電阻。
一般當(dāng)電極表面存在彌散效應(yīng)時(shí),CPE-P值總是在1~0.5之間,阻抗波特圖表現(xiàn)為向下旋轉(zhuǎn)一定角度的半圓圖。
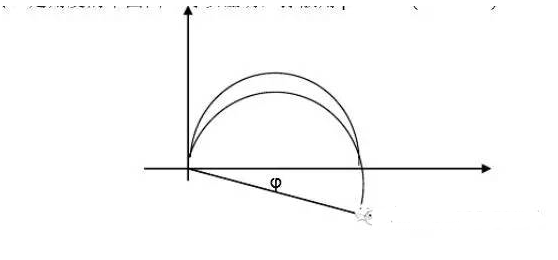
圖3具有彌散效應(yīng)的阻抗圖
可以證明,彌散角φ=π/2*(1-CPE-P),
特別有意義的是,當(dāng)CPE-P=0.5時(shí),CPE可以用來(lái)取代有限擴(kuò)散層的Warburg元件,Warburg元件是用來(lái)描述電荷通過(guò)擴(kuò)散穿過(guò)某一阻擋層時(shí)的電極行為。在極低頻率下,帶電荷的離子可以擴(kuò)散到很深的位置,甚至穿透擴(kuò)散層,產(chǎn)生一個(gè)有限厚度的Warburg元件,如果擴(kuò)散層足夠厚或者足夠致密,將導(dǎo)致即使在極限低的頻率下,離子也無(wú)法穿透,從而形成無(wú)限厚度的Warburg元件,而CPE正好可以模擬無(wú)限厚度的Warburg元件的高頻部分。當(dāng)CPE-P=0.5時(shí),

,其阻抗圖為圖3所示,一般在pH》13的堿溶液中,由于生成致密的鈍化膜,阻礙了離子的擴(kuò)散通道,因此可以觀察到圖4所示的波特圖。
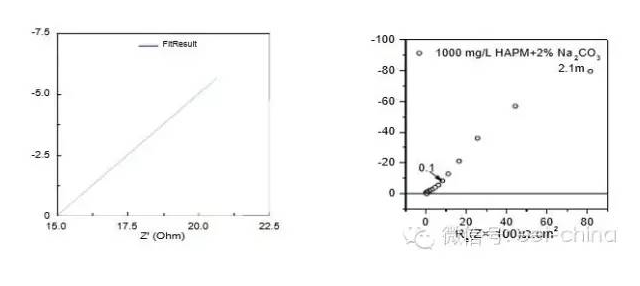
圖4.當(dāng)CPE-P為0.5時(shí)(左)及在Na2CO?3溶液中的波特圖
2.2、有限擴(kuò)散層的Warburg元件-閉環(huán)模型
本元件主要用來(lái)解析一維擴(kuò)散控制的電化學(xué)體系,其阻抗為,一般在解析過(guò)程中,設(shè)置P=0.5,并且Ws-T=L2/D,(其中L是有效擴(kuò)散層厚度,D是微粒的一維擴(kuò)散系數(shù)),計(jì)算表明,當(dāng)ω-》0時(shí),Z=R,當(dāng)ω-》+∞,在
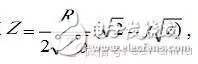
,與CPE-P=0.5時(shí)的阻抗表達(dá)式相同,阻抗圖如圖5。
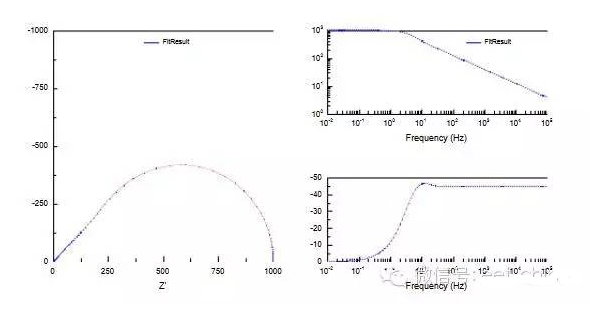
圖5.閉環(huán)的半無(wú)限的Warburg阻抗圖
2.3、有限擴(kuò)散層的Warburg元件-發(fā)散模型
本元件也是用來(lái)描述一維擴(kuò)散控制的電化學(xué)體系,其阻抗為,其中ctnh為反正且函數(shù),F(xiàn)(x)=Ln[(1+x)/(1-x)]。與閉環(huán)模型不同的是,其阻抗圖的實(shí)部在低頻時(shí)并不與實(shí)軸相交。而是向虛部方向發(fā)散。即在低頻時(shí),更像一個(gè)電容。典型的阻抗圖如圖6。
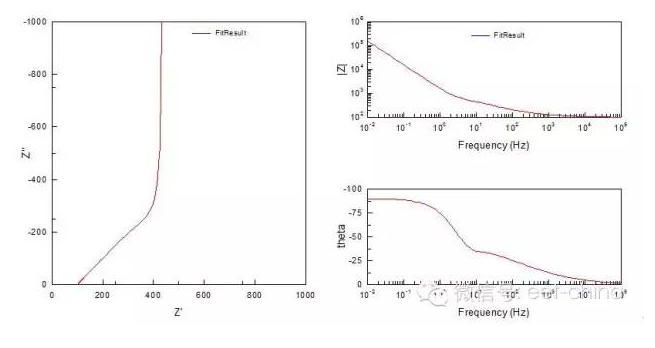
圖6.發(fā)散的半無(wú)限的Warburg阻抗圖
3、常用的等效電路圖及其阻抗圖譜
對(duì)阻抗的解析使一個(gè)十分復(fù)雜的過(guò)程,這不單是一個(gè)曲線擬合的問(wèn)題,事實(shí)上,你可以選擇多個(gè)等效電路來(lái)擬合同一個(gè)阻抗圖,而且曲線吻合的相當(dāng)好,但這就帶來(lái)了另外一個(gè)問(wèn)題,哪一個(gè)電路符合實(shí)際情況呢,這其實(shí)也是最關(guān)鍵的問(wèn)題。他需要有相當(dāng)豐富的電化學(xué)知識(shí)。需要對(duì)所研究體系有比較深刻的認(rèn)識(shí)。而且在復(fù)雜的情況下,單純依賴交流阻抗是難以解決問(wèn)題的,需要輔助以極化曲線以及其它暫態(tài)試驗(yàn)方法。
由于阻抗測(cè)量基本是一個(gè)暫態(tài)測(cè)量,所以工作電極,輔助電極以及參比電極的魯金毛細(xì)管的位置極有要求。例如魯金毛細(xì)管距離參比電極的位置不同,在阻抗圖的高頻部分就會(huì)表現(xiàn)出很大的差異,距離遠(yuǎn)時(shí),高頻部分僅出現(xiàn)半個(gè)容抗弧,距離近時(shí),高頻弧變成一個(gè)封閉的弧;當(dāng)毛細(xì)管緊挨著工作電極表面時(shí),可能會(huì)出現(xiàn)感抗弧,這其中原因還不清楚。
為了有利于大家在今后的試驗(yàn)中對(duì)阻抗圖有一個(gè)粗略的認(rèn)識(shí),下面簡(jiǎn)單將幾種常見(jiàn)阻抗圖譜介紹一下。
3.1、吸附型緩蝕劑體系
如果緩蝕劑不參與電極反應(yīng),不產(chǎn)生吸附絡(luò)合物等中間產(chǎn)物,則它的阻抗圖僅有一個(gè)時(shí)間常數(shù),表現(xiàn)為變形的單容抗弧,這是由于緩蝕劑在表面的吸附會(huì)使彌散效應(yīng)增大,同時(shí)也使雙電層電容值下降,其阻抗圖及其等效電路如圖7。
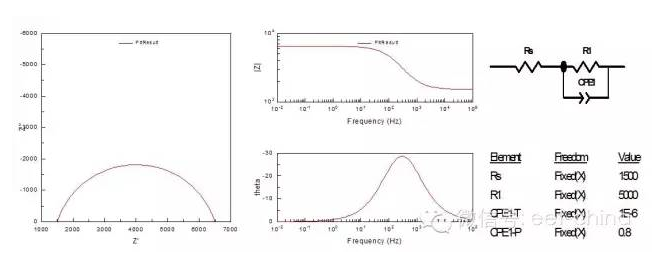
圖7.具有一個(gè)時(shí)間常數(shù)的單容抗弧阻抗圖
3.2、涂層下的金屬電極阻抗圖
涂裝金屬電極存在兩個(gè)容性時(shí)間常數(shù),一個(gè)時(shí)涂層本身的電容,另外一個(gè)是金屬表面的雙電層電容,阻抗圖上具有雙容抗弧,如圖8所示。
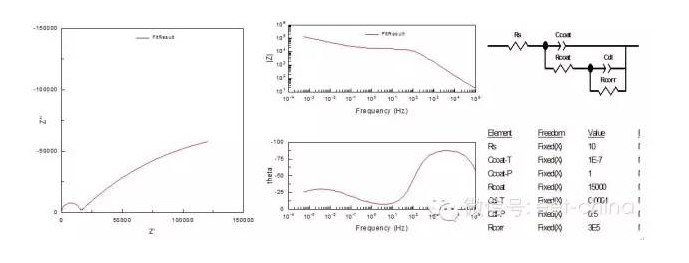
圖8.具有兩個(gè)時(shí)間常數(shù)的涂層金屬阻抗圖
等效電路中的Ccoat為涂層本身的電容,Rcoat為涂層電阻,Cdl為涂層下的雙電層電容,當(dāng)溶液通過(guò)涂層滲透到金屬表面時(shí),還會(huì)有電化學(xué)反應(yīng)發(fā)生,Rcorr為電極反應(yīng)的阻抗。
3.3、局部腐蝕的電極阻抗圖
當(dāng)金屬表面存在局部腐蝕(點(diǎn)腐蝕),點(diǎn)蝕可描述為電阻與電容的串聯(lián)電路,其中電阻Rpit為蝕點(diǎn)內(nèi)溶液電阻,一般Rpit=1~100Ω之間。而是實(shí)際體系測(cè)得的阻抗應(yīng)為電極表面鈍化面積與活化面積(即點(diǎn)蝕坑)的界面阻抗的并聯(lián)耦合。但因鈍化面積的阻抗遠(yuǎn)遠(yuǎn)高于活化免得阻抗,因而實(shí)際上阻抗頻譜圖反映了電極表面活化面積上的阻抗,即兩個(gè)時(shí)間常數(shù)疊合在一起,表現(xiàn)為一個(gè)加寬的容抗弧。其阻抗圖譜與等效電路如圖9所示。
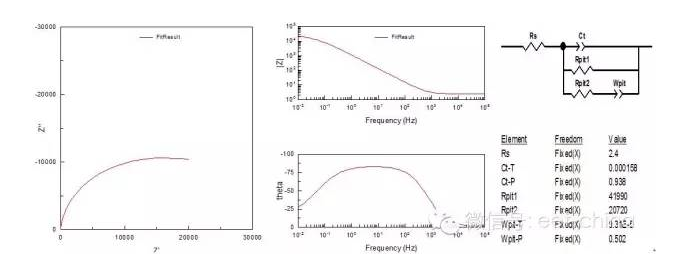
圖9.表面存在局部腐蝕時(shí)阻抗圖
3.4、半無(wú)限擴(kuò)散層厚度的電極阻抗圖
所謂半無(wú)限擴(kuò)散過(guò)程,是指溶液中的擴(kuò)散區(qū)域,即在定態(tài)下擴(kuò)散粒子的濃度梯度為一定數(shù)值的區(qū)域,擴(kuò)散層厚度為無(wú)窮大,不過(guò)一般如果擴(kuò)散層厚度大于數(shù)厘米后,即可認(rèn)為滿足這一條件。此時(shí)法拉第阻抗就等于半無(wú)限擴(kuò)散控制的濃差極化阻抗Zw與電極反應(yīng)阻抗Zf的串聯(lián),其阻抗

,電極反應(yīng)完全受擴(kuò)散步驟控制,外加的交流信號(hào)只會(huì)引起表面反應(yīng)粒子濃度的波動(dòng),且電極表面反應(yīng)粒子的濃度波動(dòng)相位角正好比交流電流落后45度,阻抗圖為45度角的傾斜直線,如圖10所示。如果法拉第阻抗中有Warburg阻抗,則Rp無(wú)窮大,但在腐蝕電位下,由于總的法拉第阻抗是陽(yáng)極反應(yīng)阻抗與陰極反應(yīng)阻抗的并聯(lián),一般僅有陰極反應(yīng)有Zw,故此時(shí)總的Rp應(yīng)為陽(yáng)極反應(yīng)的Rp1值,Zf仍為有限值。
當(dāng)電極表面存在較厚且致密的鈍化膜時(shí),由于膜電阻很大,離子的遷移過(guò)程受到極大的抑制,所以在低頻部分其阻抗譜也表現(xiàn)為一條45度傾角的斜線。
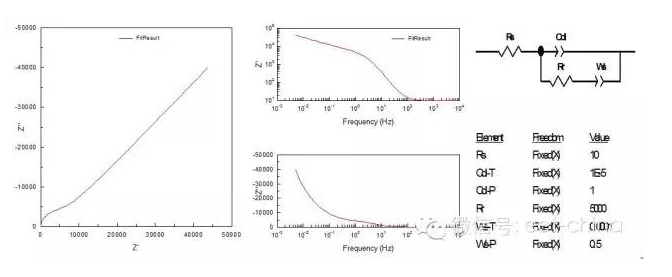
圖10.表面存在致密的鈍化膜時(shí)的阻抗圖
3.5、有限擴(kuò)散層厚度的電極阻抗圖
當(dāng)擴(kuò)散層厚度有限時(shí),即在距電極表面l處,擴(kuò)散粒子的濃度為一不隨時(shí)間變化的定值,則有
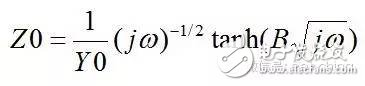
,在低頻是完全由濃差擴(kuò)散控制,但在高頻使它相當(dāng)于一個(gè)RC串聯(lián)電路,見(jiàn)2.2節(jié)。實(shí)際測(cè)量中,當(dāng)電極表面的存在擴(kuò)散層控制時(shí),在較低頻率下,離子的遷移過(guò)程可以通過(guò)延長(zhǎng)時(shí)間來(lái)擴(kuò)散到金屬表面,發(fā)生電化學(xué)反應(yīng),因此波特圖表現(xiàn)為一閉合的圓弧,可以用有限擴(kuò)散層厚度的Warburg阻抗來(lái)模擬,如圖11所示。
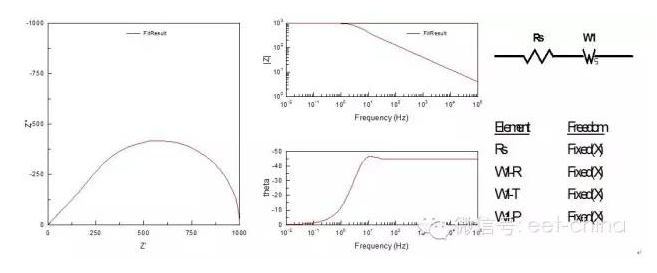
圖11.表面存在非致密的鈍化膜時(shí)的阻抗圖
3.6、同時(shí)受電化學(xué)和濃差極化控制
在混合控制下,交流信號(hào)通過(guò)電極時(shí),除了濃差極化外還將出現(xiàn)電化學(xué)極化,這時(shí)電極的法拉第阻抗比較復(fù)雜,在高頻部分為雙電層的容抗弧,而在低頻部分,擴(kuò)散控制將超過(guò)電化學(xué)控制,出現(xiàn)Warburg阻抗,其等效電路及阻抗圖如圖12所示。
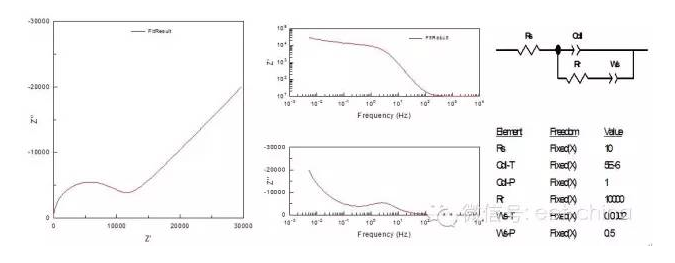
圖12.同時(shí)受擴(kuò)散和電化學(xué)控制的阻抗圖
3.7、具有雙容抗弧的電化學(xué)阻抗
另外如果法拉第電流If不僅與極化電位?E有關(guān),而且與某一表面狀態(tài)變量X相關(guān),則由于X對(duì)電位的響應(yīng)會(huì)引起弛豫現(xiàn)象,從而出現(xiàn)除雙電層電容以外的第二個(gè)時(shí)間常數(shù),不過(guò)這第二個(gè)時(shí)間常數(shù)即可能是容性的也可能是感性的,這取決于B值,當(dāng)B》0時(shí),低頻出現(xiàn)感抗弧,當(dāng)B《0時(shí),則在低頻出現(xiàn)第二個(gè)容抗弧。某些吸附型物質(zhì)在電極表面成膜后,這層吸附層覆蓋于緊密雙電層之上,且其本身就具有一定的容性阻抗Cf,它與電極表面的雙電層串聯(lián)在一起組成具有兩個(gè)時(shí)間常數(shù)的阻抗譜,其阻抗圖如圖13所示。
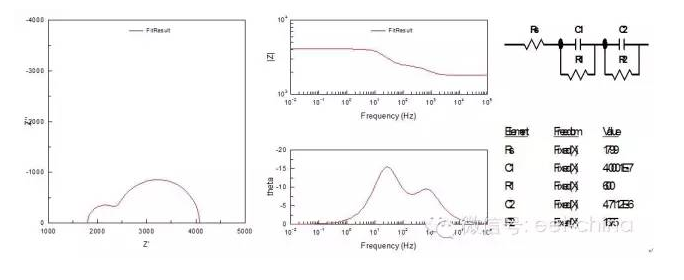
圖13.具有兩個(gè)時(shí)間常數(shù)的阻抗圖
3.8、低頻出現(xiàn)感抗弧的電化學(xué)體系
前面說(shuō)過(guò),當(dāng)法拉第電流不僅與電極電位有關(guān),而且受電極表面狀態(tài)變量X影響,而這個(gè)狀態(tài)變量本

弧。
當(dāng)電極反應(yīng)出現(xiàn)中間產(chǎn)物時(shí),這種中間產(chǎn)物吸附與金屬電極表面產(chǎn)生表面吸附絡(luò)合物,該表面絡(luò)合物產(chǎn)生于電極反應(yīng)的第一步,而消耗于第二步反應(yīng),而一般情況下,吸附過(guò)程的弛豫時(shí)間常數(shù)要比電雙層電容Cdl與Rt組成的充放電過(guò)程的弛豫時(shí)間常數(shù)RtCdl大的多,因此在阻抗圖的低頻部分會(huì)出現(xiàn)感抗弧。如圖14所示。
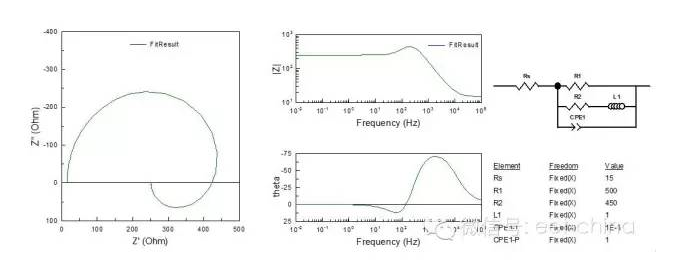
圖14.低頻出現(xiàn)感抗弧的阻抗圖

電容,整個(gè)EIS出現(xiàn)兩個(gè)容抗弧,如圖13所示。
混合電位下的阻抗譜特征
上面所述的阻抗譜均是在自然電位下測(cè)量的,而電極反應(yīng)在自然電位下同時(shí)具有陰陽(yáng)極兩個(gè)反應(yīng),所以阻抗譜所反映的是兩個(gè)電極反應(yīng)的頻譜特征,即文獻(xiàn)所述的混合電位下的阻抗譜,當(dāng)沒(méi)有狀態(tài)變量時(shí),EIS仍只有一個(gè)時(shí)間常數(shù),當(dāng)有一個(gè)狀態(tài)變量影響電極反應(yīng)速度時(shí),阻抗譜會(huì)出現(xiàn)兩個(gè)時(shí)間常數(shù)。不過(guò)在某些情況下,需要研究單一陽(yáng)極反應(yīng)特征,就必須將研究電極的電位極化(弱極化區(qū))到不同的陽(yáng)極電位下進(jìn)行阻抗測(cè)量,以抑制陰極反應(yīng),這就是所謂的直流偏壓下的阻抗測(cè)試,這一點(diǎn)在研究鈍化膜的臨界破裂電位下的阻抗特征尤為重要,它能提供點(diǎn)蝕誘發(fā)期的重要特征,另外在研究緩蝕劑的陽(yáng)極脫附行為時(shí)也十分重要。
交流阻抗的不足之處
前面指出,對(duì)于同一組抗譜,可以找到不止一個(gè)電路能滿足它的解析,而對(duì)于同一個(gè)電路,當(dāng)電路中的元件參數(shù)不同時(shí),可以得到完全不同類型的阻抗譜,因此依靠等效電路來(lái)推測(cè)電極過(guò)程的動(dòng)力學(xué)機(jī)構(gòu)是一個(gè)不可靠的方法。
 電子發(fā)燒友App
電子發(fā)燒友App









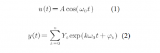


















評(píng)論