蒙哥馬利(Montgomery)冪模運算是快速計算a^b%k的一種算法,是RSA加密算法的核心之一。
蒙哥馬利模乘的優點在于減少了取模的次數(在大數的條件下)以及簡化了除法的復雜度(在2的k次冪的進制下除法僅需要進行左移操作)。模冪運算是RSA 的核心算法,最直接地決定了RSA 算法的性能。
針對快速模冪運算這一課題,西方現代數學家提出了大量的解決方案,通常都是先將冪模運算轉化為乘模運算。
這里為大家梳理一下整個蒙哥馬利算法的本質,蒙哥馬利算法并不是一個獨立的算法,而是三個相互獨立又相互聯系的算法集合,其中包括
蒙哥馬利乘模,是用來計算x?y (mod N)
蒙哥馬利約減,是用來計算t?ρ?1 (mod N)
蒙哥馬利冪模,是用來計算xy (mod N)
其中蒙哥馬利冪乘是RSA加密算法的核心部分。
基本概念
梳理幾個概念,試想一個集合是整數模N之后得到的
ZN={0,1,2,?,N?1}
注:N在base-b進制下有lN位。 比如10進制和100進制,都屬于base-10進制,因為100=102,所以b=10。在10進制下,667的lN=3這樣的集合叫做N的剩余類環,任何屬于這個集合Z的x滿足以下兩個條件:
1. 正整數
2. 最大長度是lN
文中講到的蒙哥馬利算法就是用來計算基于ZN集合上的運算,簡單講一下原因,因為RSA是基于大數運算的,通常是1024bit或2018bit,而我們的計算機不可能存儲完整的大數,因為占空間太大,而且也沒必要。因此,這種基于大數運算的加密體系在計算的時候都是基于ZN集合的,自然,蒙哥馬利算法也是基于ZN。
在剩余類環上,有兩種重要的運算,一類是簡單運算,也就是加法和減法,另一類復雜運算,也就是乘法。我們比較熟悉的是自然數集上的運算,下面看下怎么從自然數集的運算演變成剩余類環上的運算。
對于加法運算,如果計算x±y (mod N) (0≤x,y<N),試想自然數集上的 x±y
0≤x+y≤2?(N?1)
?(N?1)≤x?y≤(N?1)我們可以簡單的通過加減N來實現從自然數到剩余類集的轉換
另外一類是乘法操作,也就是x?y (mod N)(0≤x,y<N),那么
0≤x?y≤(N?1)2如果在自然數集下,令t=x?y,那么對于modN我們需要計算
t?(N??t/N?)加減操作很簡單,具體的算這里就不細說了,我們用ZN?ADD 來代表剩余類環上的加法操作。既然我們可以做加法操作,那么我們就可以擴展到乘法操作,算法如下
但是這并不是一個好的解決方案,因為通常來說,我們不會直接做w位乘w位的操作,這個后面會用蒙哥馬利的乘法來代替解決。
對于取模操作,一般有以下幾種方法
1,根據以下公式,來計算取模操作
t?(N??t/N?)
這種解法有以下特征
整個計算過程是基于標準的數字表示
不需要預計算(也就是提前計算一些變量,以備使用)
涉及到一個除法操作,非常費時和復雜
2,用Barrett reduction算法,這篇文章不細說,但是有以下特征
基于標準的數字表示
不需要預計算
需要2?(lN+1)?(lN+1) 次數乘運算
3,用蒙哥馬利約減,也就是下面要講的算法,有以下特征
不是基于標準的數字表示(后文中有提到,是基于蒙哥馬利表示法)
需要預計算
需要2?(lN)?(lN) 次數乘運算
蒙哥馬利預備知識
在將蒙哥馬利算法之前,先看一下在自然數下的乘法公式
計算x?y,想象一下我們常用的計算乘法的方法,用乘數的每一位乘上被乘數,然后把得到的結果相加,總結成公式,可以寫成如下的形式。
x?y=x?sumly?1i=0yi?bi
=sumly?1i=0yi?x?bi
嘗試下面一個例子,10進制下(也就是b=10),y=456(也就是ln=3),計算x?y,公式可演變如下:
x?y=(y0?x?100)+(y1?x?101)+(y2?x?102)
=(y0?x?0)+(y1?x?10)+(y2?x?100)
=(y0?x)+10?(y1?x+10?(y2?x?+10?(0)))
最后一次演變其實就是用霍納法則(Horner’s rule)所講的規則,關于霍納法則,可以自行百度。
這個計算過程寫成代碼實現的算法應該是這樣的:
接下來我們來看下面這樣的計算,計算(x?y)/1000,由前面可以知道
x?y=(y_0?x)+10?(y_1?x+10?(y_2?x?+10?(0)))
由此可以知道:
這個計算過程寫成代碼實現的算法是這樣的:
接下來我們再來看在剩余類集合下的乘法操作 x?y/1000 (mod 667)
我們知道剩余類集合Z667={0,1?666},是不存在小數的,而如果我們采用自然數集的計算方式的話,就會出現小數,比如前面的例子,除10就會有小數。
這個問題是這樣的,我們知道u?667≡0(mod667)(≡表示取模相等),所以我們可以選擇一個合適的u,用u乘667再加上r,使得和是一個可以除10沒有小數,這樣在mod 667之后依然是正確的結果。至于u怎么算出來,這篇文章會在后面的章節說明。
這個過程之后x?y/1000 (mod 667) 的計算算法可以寫成如下的形式
至此,你可能還不明白上面說這一堆演變的原因,其實很簡單,原來是一個(x?y) (mod 667)的運算,這個運算中的模操作,正常情況下是要通過除法實現的,而除法是一個特別復雜的運算,要涉及到很多乘法,所以在大數運算時,我們要盡量避免除法的出現。而通過以上幾個步驟,我們發現(x?y)/1000 (mod 667)這個操作是不用除法的。等等,算法中明明有個除10的操作,你騙誰呢。不知道你有沒有發現,除數其實是我們的進制數,除進制數在計算機中是怎么做呢,其實很簡單,左移操作就ok了。所以這個計算方法是不涉及到除法操作的。
但是我們要計算的明明是(x1?y1) (mod 667),怎么現在變成了(x2?y2)/1000 (mod 667),所以在下一步,我們要思考的是怎么樣讓(x1?y1) (mod 667)轉變成(x2?y2)/1000 (mod 667)這種形式。
考慮這樣兩個算法
- 第一個是輸入x和y,計算x?y?ρ?1
- 第二個算法,輸入一個t,計算t?ρ?1。
x?y (mod 667)=((x?1000)?(y?1000)/1000)/1000 (mod 667)
是不是變成了我們需要的(x?y)/1000 (mod 667)模式,而且這個轉變過程是不是可以通過上面兩個算法來實現,輸入值如果是(x?1000)和(y?1000),則通過第一個算法可以得到((x?1000)?(y?1000)/1000),把結果作為第二個算法的輸入值,則通過第二個算法可以得到((x?1000)?(y?1000)/1000)/1000。
? ? ? ? 算法的詳解
扯了一大頓,終于引出了今天文章的主角,前面講到的兩個算法,第一個就是蒙哥馬利乘模,第二個就是蒙哥馬利約減。下面我們來講這兩個算法的詳解。
正如前面提到的蒙哥馬利算法的三個特性之一是,不是基于普通的整數表示法,而是基于蒙哥馬利表示法。什么是蒙哥馬利表示法呢,其實也很簡單,上面我們提到,要讓(x1?y1) (mod 667)轉變成(x2?y2)/1000 (mod 667)這種形式,我們需要將輸入參數變成(x?1000)和(y?1000),而不是x和y本身,而(x?1000)和(y?1000) 其實就是蒙哥馬利表示法。
所以我們先定義幾個概念:
蒙哥馬利參數
給定一個N,N在b進制(例如,二進制時,b=2)下共有l位,gcd(N,b)=1,先預計算以下幾個值(這就是前面提到的特性之一,需要預計算):
ρ=bk 指定一個最小的k,使得bk》N
ω=?N?1(mod ρ)
這兩個參數是做什么用的呢,你對照前面的演變過程可以猜到ρ 就是前面演變中的1000,而ω 則是用來計算前面提到的u的。
蒙哥馬利表示法
對于x,0≤x≤N?1,x的蒙哥馬利表示法表示為x=x?ρ (mod N)
蒙哥馬利約減
蒙哥馬利約減的定義如下
給定一些整數t,蒙哥馬利約減的計算結果是t?ρ?1 (mod N)
蒙哥馬利約減的算法可表示為
蒙哥馬利約減可以算作是下面要說的蒙哥馬利模乘當x=1時的一種特殊形式,。同時它又是蒙哥馬利乘模要用到的一部分,這在下一部分講蒙哥馬利乘模的時候有講到。
蒙哥馬利約減可以用來計算某個值得取模操作,比如我們要計算m(mod N),只需要將m
的蒙哥馬利表示法m?ρ作為參數,帶入蒙哥馬利約減,則計算結果就是m(mod N)。
蒙哥馬利乘模
一個蒙哥馬利乘模包括整數乘法和蒙哥馬利約減,現在我們有蒙哥馬利表示法:
x^=x?ρ (mod N)
y^=y?ρ (mod N)
它們相乘的結果是
t=x^?y^
=(x?ρ)?(y?ρ)
=(x?y)?ρ2
最后,用一次蒙哥馬利約減得到結果
t^=(x?y)?ρ (mod N)
上面我們可以看出,給出的輸入參數是x^ 和y^, 得到的結果是(x?y)?ρ (mod N),所以蒙哥馬利乘法也可以寫成如下形式,已知輸入參數x和y,蒙哥馬利乘法是計算(x?y)?ρ?1 (mod N)
舉個例子:
b=10,也就是說在10進制下,N=667
讓bk》N的最小的k是3,所以ρ=bk=103=1000
ω=?N?1 (mod ρ)=?667?1 (mod ρ)=997
因為x=421,所以x^=x?ρ(mod N)=421?1000(mod 667)=123
因為y=422,所以y^=y?ρ(mod N)=422?1000(mod 667)=456
所以計算x^和y^蒙哥馬利乘結果是
x^?y^?ρ?1=(421?1000?422?1000)?1000?1 (mod 667)
(421?422)?1000 (mod 667)
(240)?1000 (mod 667)
547 (mod 667)
然后總結一下蒙哥馬利約減和蒙哥馬利乘法的偽代碼實現,這個算法其實就是從蒙哥馬利預備知識講到的算法演變來的。
上面的例子用這個算法可以描述為
蒙哥馬利算法是一套很完美的算法,為什么這么說呢,你看一開始已知x,我們要求x^=x?ρ,這個過程可以通過蒙哥馬利乘法本身來計算,輸入參數x和ρ2,計算結果就是x^=x?ρ。然后在最后,我們知道x^=x?ρ,要求得x的時候,同樣可以通過蒙哥馬利算法本身計算,輸入參數x^和1,計算結果就是x。有沒有一種因就是果,果就是因的感覺,這就是為什么說蒙哥馬利算法是一套很完美的算法。
蒙哥馬利冪模
最后,才說到我們最開始提到的RSA的核心冪模運算,先來看一下普通冪運算的算法是怎么得出來的。
以下資料來自于百度百科快速模冪運算
針對快速模冪運算這一課題,西方現代數學家提出了大量的解決方案,通常都是先將冪模運算轉化為乘模運算。
例如求D=C^15%N
由于:a*b % n = (a % n)*(b % n) % n
所以令:
C1 =C*C % N =C^2 % N
C2 =C1*C % N =C^3 % N
C3 =C2*C2 % N =C^6 % N
C4 =C3*C % N =C^7 % N
C5 =C4*C4 % N =C^14 % N
C6 =C5*C % N =C^15 % N
即:對于E=15的冪模運算可分解為6 個乘模運算,歸納分析以上方法可以發現:
對于任意指數E,都可采用以下算法計算D=C**E % N:
D=1
WHILE E》0
IF E%2=0
C=C*C % N
E=E/2
ELSE
D=D*C % N
E=E-1
RETURN D
繼續分析會發現,要知道E 何時能整除 2,并不需要反復進行減一或除二的操作,只需驗證E 的二進制各位是0 還是1 就可以了,從左至右或從右至左驗證都可以,從左至右會更簡潔,
設E=Sum[i=0 to n](E*2**i),0《=E《=1
則:
D=1
FOR i=n TO 0
D=D*D % N
IF E=1
D=D*C % N
RETURN D這樣,模冪運算就轉化成了一系列的模乘運算。
算法可以寫成如下的形式
如果我們現在用蒙哥馬利樣式稍作改變,就可以變成如下的形式:
以上就是蒙哥馬利算法的全部,通過蒙哥馬利算法中的約減運算,我們將大數運算中的模運算變成了移位操作,極大地提高了大數模乘的效率。
但是在以上的算法,可以發現還有兩個變量的計算方式不是很清楚,一個是ω,前面說過ω=?N?1(modN) ,其實在算法中,我們看到,omega僅僅被用來做modb操作,所以事實上,我們只需要計算modb即可。
盡管N有可能是合數(因為兩個素數的乘積不一定是素數),但通常N和ρ(也就是N和b)是互質的,也就是說N?(b)=1(mob b)(費馬定理),N?(b)?1=N?1(mob b)
因為b=2ω,所以?(b)=2(ω?1),寫成算法是這樣的
還有一個參數是ρ2,還記得前面說過ρ是怎么得出來嗎,選定一個最小的k,使得bk》N,我們還知道N在b進制下是lN位,所以當k=lN的時候肯定是符合要求。
b=2ω 所以ρ=bk=(2ω)kρ2=(2w)k)2=22?k?ω=22?lN?ω,算法如下
至此整個蒙哥馬利算法就全部說完了。通過這個算法,我們可以實現快速冪模。
C++實現
inline unsigned __int64 MulMod(unsigned __int64 a, unsigned __int64 b, unsigned __int64 n)
{
return a * b % n;
}
/*
模冪運算,返回值 x=base^pow mod n
*/
unsigned __int64 PowMod(unsigned __int64 base, unsigned __int64 pow, unsigned __int64 &n)
{
unsigned __int64 a=base, b=pow, c=1;
while(b)
{
while(!(b & 1))
{
b》》=1; //a=a * a % n; //
a=MulMod(a, a, n);
} b--; //c=a * c % n; //
c=MulMod(a, c, n);
} return c;
}
? ? ? ?數論學家利用費馬小定理研究出了多種素數測試方法,目前最快的算法是拉賓
米勒測試算法,其過程如下:
(1)計算奇數M,使得N=(2**r)*M+1
(2)選擇隨機數A《N
(3)對于任意i《r,若A**((2**i)*M) % N = N-1,則N通過隨機數A的測試
(4)或者,若A**M % N = 1,則N通過隨機數A的測試
(5)讓A取不同的值對N進行5次測試,若全部通過則判定N為素數
若N 通過一次測試,則N 不是素數的概率為 25%,若N 通過t 次測試,則N 不是素數的概率為1/4**t。事實上取t 為5 時,N 不是素數的概率為 1/128,N 為素數的概率已經大于99.99%。
在實際應用中,可首先用300—500個小素數對N 進行測試,以提高拉賓米勒測試通過的概率,從而提高整體測試速度。而在生成隨機素數時,選取的隨機數最好讓r=0,則可省去步驟(3) 的測試,進一步提高測試速度。
素數測試是RSA 選取秘鑰的第一步,奇妙的是其核心運算與加解密時所需的運算完全一致:都是模冪運算。而模冪運算過程中中所需求解的歐幾里德方程又恰恰正是選取密鑰第二步所用的運算。可見整個RSA 算法具有一種整體的和諧。
 電子發燒友App
電子發燒友App
















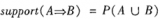














評論