霍夫曼壓縮算法概述
霍夫曼壓縮算法的主要思想是用較少的比特表示出現頻率較高的字符,用較多的比特表示出現頻率較低的字符。如下圖所示,
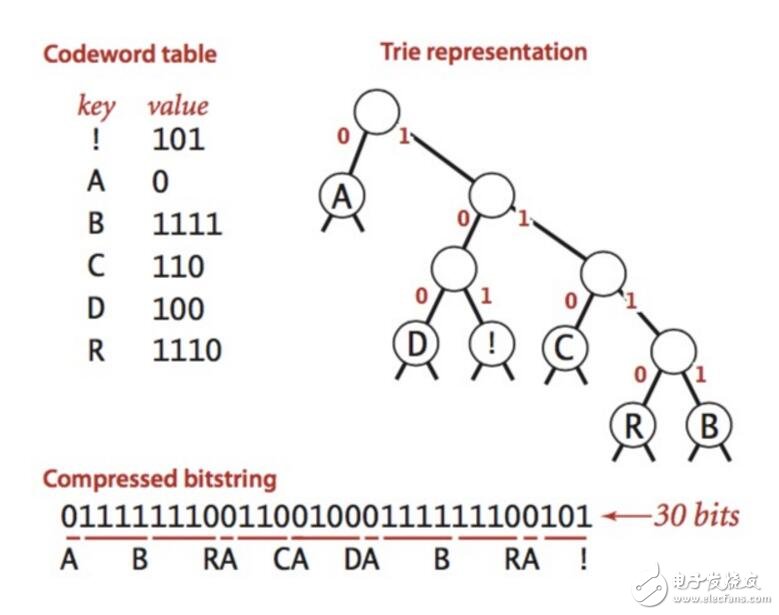
霍夫曼壓縮算法實現
①讀入完整的輸入流,并轉化為字符數組。
②計算每個字符出現的次數
③構建Huffman樹
④構建編譯表
⑤將單詞查找樹編碼成比特輸出串并寫入到輸出流
⑥將單詞總數編碼成比特輸出串并寫入到輸出流
⑦使用編譯表翻譯每個輸入字符
12345678
霍夫曼壓縮算法節點的表示
private static final int R = 256; //字符為ASCII表示
private static class Node implements Comparable《Node》 {
private final char ch;
private final int freq;
private final Node left, right;
public Node(char ch, int freq, Node left, Node right) {
this.freq = freq;
this.ch = ch;
this.left = left;
this.right = right;
}
private boolean isLeaf() {
return left == null && right == null;
}
@Override
public int compareTo(Node that) {
return this.freq - that.freq;
}
}
123456789101112131415161718192021222324252627
構建Huffman單詞查找樹
構建初始有一堆沒有父節點的節點,將它們放到最小隊列中,這樣對頭總是freq為最小的那個節點。
從隊列中找到freq最小的兩個節點,創建一個它們的父節點,將三個節點歸并成一個大節點,接著放入隊列中,
循環往復直至隊列中只剩一個節點。
/**
* @param freq 字符出現的次數
* @return
*/
private static Node buildTrie(char[] freq) {
MinPQ《Node》 pq = new MinPQ《Node》();
//初始化多個將構成一顆Huffman樹的結點
for (char i = 0; i 《 R; i++) {
if (freq[i] 》 0) pq.insert(new Node(i, freq[i], null, null));
}
// special case in case there is only one character with a nonzero frequency
if (pq.size() == 1) {
if (freq[‘\0’] == 0) pq.insert(new Node(‘\0’, 0, null, null));
else pq.insert(new Node(‘\1’, 0, null, null));
}
//歸并兩個小樹
while (pq.size() 》 1) {
Node left = pq.delMin();
Node right = pq.delMin();
Node parent = new Node(‘\0’, left.freq + right.freq, left, right); //創建連接子樹的中間結點
pq.insert(parent);
}
return pq.delMin();
}123456789101112131415161718192021222324252627282930
將Huffman單詞查找樹轉化成字節流寫到壓縮文件中
做如下規定:
中間結點寫0;葉子結點寫1,并在后面寫結點上的字符。
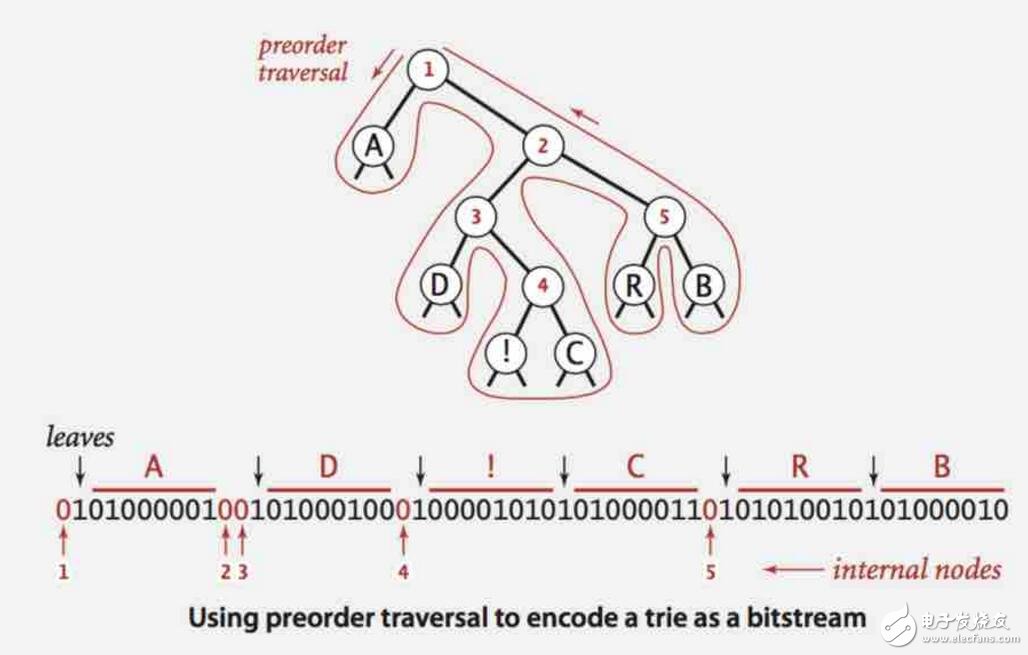
/**
* 將單詞查找樹編碼成比特輸出串并寫入到輸出流
* 用前序遍歷
*/
private static void writeTrie(Node x) {
if (x.isLeaf()) {
BinaryStdOut.write(true);
BinaryStdOut.write(x.ch);
return;
}
BinaryStdOut.write(false);
writeTrie(x.left);
writeTrie(x.right);
}
12345678910111213141516
將壓縮文件中字節流轉化為Huffman單詞查找樹
按寫入時的規定解析字節流。
/**
* 讀比特流,得出一顆單詞查找樹
*/
private static Node readTrie() {
if (BinaryStdIn.readBoolean()) { //讀到1,說明是葉子結點
return new Node(BinaryStdIn.readChar(), 0, null, null);
}
//讀到的是0,說明是中間結點,需要遞歸直到讀到1為止
Node left = readTrie();
Node right = readTrie();
return new Node(‘\0’, 0, left, right);
}
123456789101112131415
構建編譯表
構建編譯表st,索引為字符,值為路徑(比特字符串)。
根據這張表,可以將源文件中的某個字符,壓縮為更少bit表示的Huffman樹上的路徑。
private static void buildCode(String[] st, Node x, String s) {
if (!x.isLeaf()) {
buildCode(st, x.left, s + “0”);
buildCode(st, x.right, s + “1”);
} else {
st[x.ch] = s;
}
}
12345678910
壓縮
/**
* 從輸入流中讀字節流,并將壓縮后的結果寫入輸出流
*/
private static void compress() {
//①讀入完整的輸入流,并轉化為字符數組
String s = BinaryStdIn.readString();
char[] input = s.toCharArray();
//②計算每個字符出現的次數,沒有出現的就為0
char[] freq = new char[R];
for (int i = 0; i 《 input.length; i++) {
freq[input[i]]++;
}
//③構建Huffman樹
Node root = buildTrie(freq);
//④構建編譯表,將輸入中的每個char值與一個比特字符串(即Huffman樹上路徑)相關聯
String st[] = new String[R];
buildCode(st, root, “”);
//⑤將單詞查找樹編碼成比特輸出串并寫入到輸出流
writeTrie(root);
//⑥將單詞總數編碼成比特輸出串并寫入到輸出流
BinaryStdOut.write(input.length);
//⑦使用編譯表翻譯每個輸入字符
for (int i = 0; i 《 input.length; i++) {
String code = st[input[i]]; //code表示Huffman單詞查找數上的路徑
for (int j = 0; j 《 code.length(); j++) { //要一位一位地輸出
if (code.charAt(j) == ‘1’) {
BinaryStdOut.write(true);
} else {
BinaryStdOut.write(false);
}
}
}
BinaryStdOut.close();
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
### 解壓
/**
* 解壓
* 讀取壓縮文件的比特流,
* 將比特流對應為路徑在單詞查找樹上找,將找到的結點中的字符寫出
*/
private static void expand() {
Node root = readTrie();
int N = BinaryStdIn.readInt(); //讀出存在壓縮文件中的字符串長度
for (int i = 0; i 《 N; i++) { //找出源文件中每個字符
Node x = root;
while (!x.isLeaf()) { //遍歷,知道葉子結點
if (BinaryStdIn.readBoolean()) {
x = x.right;
} else {
x = x.left;
}
}
BinaryStdOut.write(x.ch);
}
BinaryStdOut.close();
}
 電子發燒友App
電子發燒友App






















評論