下面干什么？我們需要計算縱截距b。我們會在下一個教程中處理它，并完成完整的最佳擬合直線計算。它比斜率更佳易于計算，嘗試編寫你自己的函數來計算它。如果你做到了，也不要跳過下一個教程，我們會做一些別的事情。

計算縱截距

歡迎閱讀第九篇教程。我們當前正在為給定的數據集，使用 Python 計算回歸或者最佳擬合直線。之前，我們編寫了一個函數來計算斜率，現在我們需要計算縱截距。我們目前的代碼是：
from statistics import mean
import numpy as np

xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)

def best_fit_slope(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))
return m

m = best_fit_slope(xs,ys)
print(m)

請回憶，最佳擬合直線的縱截距是：

這個比斜率簡單多了。我們可以將其寫到同一個函數來節省幾行代碼。我們將函數重命名為best_fit_slope_and_intercept。

下面，我們可以填充b = mean(ys) - (m*mean(xs))，并返回m, b：
def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))

b = mean(ys) - m*mean(xs)

return m, b

現在我們可以調用它：
best_fit_slope_and_intercept(xs,ys)

我們目前為止的代碼：
from statistics import mean
import numpy as np

xs = np.array([1,2,3,4,5], dtype=np.float64)
ys = np.array([5,4,6,5,6], dtype=np.float64)

def best_fit_slope_and_intercept(xs,ys):
m = (((mean(xs)*mean(ys)) - mean(xs*ys)) /
((mean(xs)*mean(xs)) - mean(xs*xs)))

b = mean(ys) - m*mean(xs)

return m, b

m, b = best_fit_slope_and_intercept(xs,ys)

print(m,b)
# 0.3, 4.3

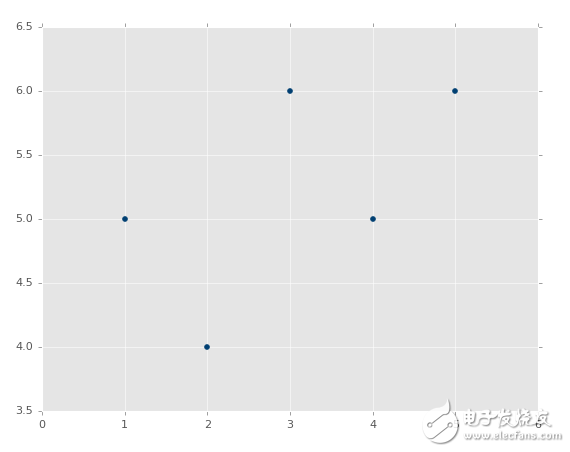
現在我們僅僅需要為數據創建一條直線：

?

要記住y=mx+b，我們能夠為此編寫一個函數，或者僅僅使用一行的for循環。
regression_line = [(m*x)+b for x in xs]

上面的一行for循環和這個相同：
regression_line = []
for x in xs:
regression_line.append((m*x)+b)

好的，讓我們收取我們的勞動果實吧。添加下面的導入：
import matplotlib.pyplot as plt
from matplotlib import style
style.use('ggplot')

我們可以繪制圖像，并且不會特備難看。現在：
plt.scatter(xs,ys,color='#003F72')
plt.plot(xs, regression_line)
plt.show()

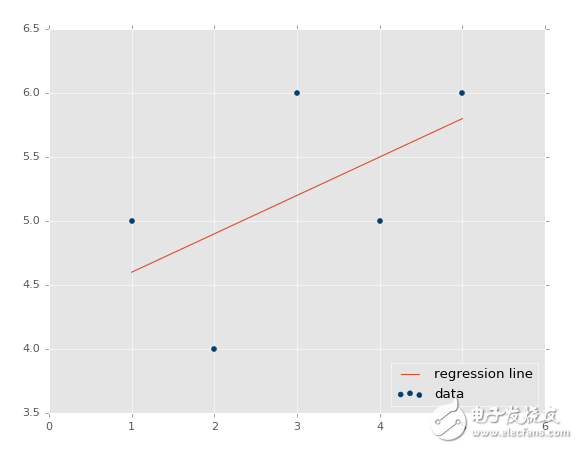
首先我們繪制了現有數據的散點圖，之后我們繪制了我們的回歸直線，之后展示它。如果你不熟悉，可以查看 Matplotlib 教程集。

輸出：

?

所以，如何基礎這個模型來做一些實際的預測呢？很簡單，你擁有了模型，只要填充x就行了。例如，讓我們預測一些點：
predict_x = 7

我們輸入了數據，也就是我們的特征。那么標簽呢？
predict_y = (m*predict_x)+b
print(predict_y)
# 6.4

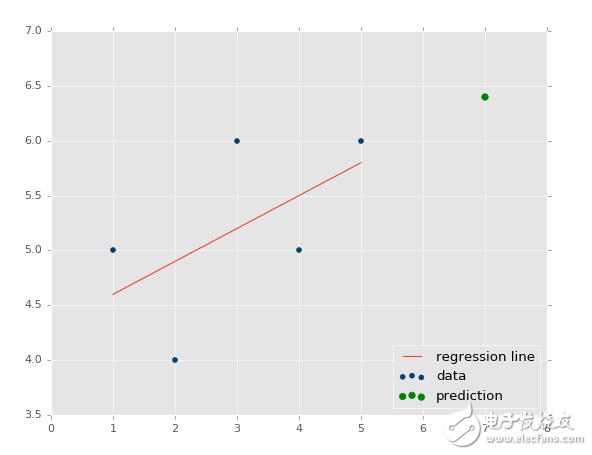
我們也可以繪制它：
predict_x = 7
predict_y = (m*predict_x)+b

plt.scatter(xs,ys,color='#003F72',label='data')
plt.plot(xs, regression_line, label='regression line')
plt.legend(loc=4)
plt.show()

輸出：

?

我們現在知道了如何創建自己的模型，這很好，但是我們仍舊缺少了一些東西，我們的模型有多精確？這就是下一個教程的話題了。

R 平方和判定系數原理

歡迎閱讀第十篇教程。我們剛剛完成了線性模型的創建和處理，現在我們好奇接下來要干什么。現在，我們可以輕易觀察數，并決定線性回歸模型有多么準確。但是，如果你的線性回歸模型是拿神經網絡的 20 個層級做出來的呢？不僅僅是這樣，你的模型以步驟或者窗口工作，也就是一共 5 百萬個數據點，一次只顯示 100 個，會怎么樣？你需要一些自動化的方式來判斷你的最佳擬合直線有多好。

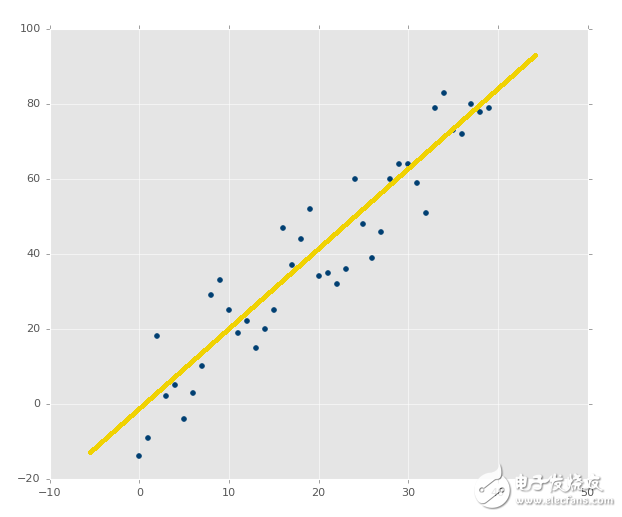
回憶之前，我們展示幾個繪圖的時候，你已經看到，最佳擬合直線好還是不好。像這樣：

?

與這個相比：

?

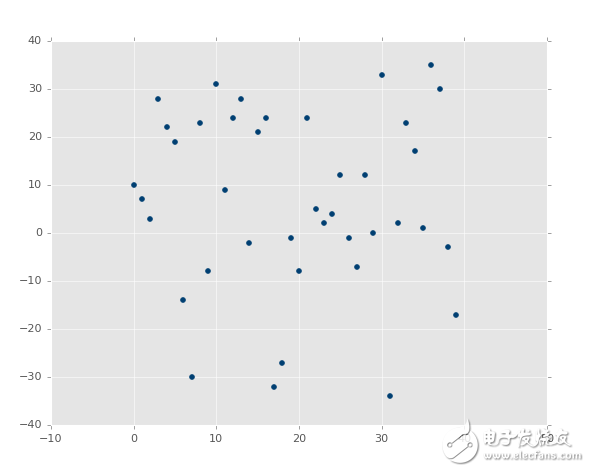
第二張圖片中，的確有最佳擬合直線，但是沒有人在意。即使是最佳擬合直線也是沒有用的。并且，我們想在花費大量計算能力之前就知道它。