基于深度強化學習的智能船舶航跡跟蹤控制
人工智能技術與咨詢 昨天
本文來自《中國艦船研究》?,作者祝亢等
關注微信公眾號:人工智能技術與咨詢。了解更多咨詢!
0.?? 引 言
目前,國內外對運載工具的研究正朝著智能化、無人化方向發展,智能船舶技術受到全球造船界與航運界的廣泛關注。其以實現船舶航行環境的智能化、自主化發展為目標,深度融合傳統船舶設計與制造技術以及現代信息通信與人工智能技術,包含智能航行、智能船用設備、智能船舶測試等多方面的研究[1]。其中,智能航行技術一直是保障船舶順利完成貨物運輸、通信救助等任務的重要基礎。要使船舶在面對多種復雜水域干擾的情況下也能遵守正常的通航秩序,安全地執行任務且保證完成效果,采取有效的控制手段精確進行航跡跟蹤就顯得尤為重要。
針對航跡跟蹤的研究任務可以分為制導和控制2個方面。在制導方面,常由視線(line-of-sight,LOS)算法將路徑跟蹤問題轉換為方便處理的動態誤差控制問題;在控制方面,基于船舶的復雜非線性系統,常考慮使用PID等無模型控制方法,或采用模型線性化的方法來解決非線性模型在計算速率方面存在的問題。但對于復雜的環境,傳統PID控制器不僅參數復雜,還不具備自適應學習能力。而最優控制、反饋線性化一類的控制算法通常需要建立精確的模型才能獲得較高的控制精度。滑模控制雖然對模型精度要求不高,但其抖振問題難以消除[2]。即使存在一些自適應參數調節方法,如通過估計系統輸出實現PID參數自整定的自適應PID控制方法,也會由于模型的不確定性和外界擾動,存在系統輸出與真實輸出的偏差[3],又或者存在參數尋優時間過長的問題而影響控制的實時性。對于與模糊邏輯相結合的響應速度快、實時性好的PID自適應控制器[4],其控制精度依賴于復雜的模糊規則庫,致使整體計算復雜。
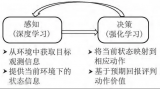
考慮到船舶的復雜非線性系統模型,和保障航跡跟蹤控制的實時性時產生的大量參數整定和復雜計算等問題,本文將采用深度強化學習算法來研究智能船舶的軌跡跟蹤問題。深度強化學習(deep reinforcement learning,DRL)是深度學習與強化學習的結合,其通過強化學習與環境探索得到優化的目標,而深度學習則給出運行的機制用于表征問題和解決問題。深度強化學習算法不依賴動力學模型和環境模型,不需要進行大量的算法計算,還具備自學習能力。Magalh?es等[5]基于強化學習算法,使用Q-learning設計了一種監督開關器并應用到了無人水面艇,它能智能地切換控制器從而使無人艇的行駛狀態符合多種環境與機動要求。2015年,Mnih等[6]為解決復雜強化學習的穩定性問題,將強化學習與深度神經網絡相結合,提出了深度Q學習(deep Q network,DQN)算法,該算法的提出代表了深度強化學習時代的到來。之后,在欠驅動無人駕駛船舶的航行避碰中也進行了相關應用[7]。
面對存在的大量參數整定、復雜算法計算等問題,為實現船舶航跡跟蹤的精準控制,本文擬設計一種基于深度確定性策略梯度算法(deep deterministic policy gradient,DDPG)的深度強化學習航跡跟蹤控制器,在LOS算法制導的基礎上,對船舶航向進行控制以達到航跡跟蹤效果。然后,根據實際船舶的操縱特性以及控制要求,將船舶路徑跟蹤問題建模成馬爾可夫決策過程,設計相應的狀態空間、動作空間與獎勵函數,并采用離線學習方法對控制器進行學習訓練。最后,通過仿真實驗驗證深度強化學習航跡控制器算法的有效性,并與BP-PID控制器算法的控制效果進行對比分析。
1.?? 智能船舶航跡跟蹤控制系統總體設計
1.1?? LOS算法制導
航跡跟蹤控制系統包括制導和控制2個部分,其中制導部分一般是根據航跡信息和船舶當前狀態確定所需的設定航向角值來進行工作。本文使用的LOS算法已被廣泛運用于路徑控制。LOS算法可以在模型參數不確定的情況下,以及在復雜的操縱環境中與控制器結合,從而實現對模型的跟蹤控制。視線法的導航原理是基于可變的半徑與路徑點附近生成的最小圓來產生期望航向,即LOS角。經過適當的控制,使當前船舶的航向與LOS角一致,即能達到航跡跟蹤的效果[8]。
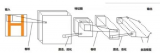
LOS算法示意圖如圖1所示。假設當前跟蹤路徑點為Pk+1(xk+1,yk+1)Pk+1(xk+1,yk+1),上一路徑點為Pk(xk,yk)Pk(xk,yk),以船舶所在位置Ps(xs,ys)Ps(xs,ys)為圓心,選擇半徑RLosRLos與路徑PkPk+1PkPk+1相交,選取與Pk+1Pk+1相近的點PLos(xLos,yLos)PLos(xLos,yLos)作為LOS點,當前船舶坐標到LOS點的方向矢量與x0x0的夾角ψLosψLos則為需要跟蹤的LOS角。圖中:dd為當前船舶至跟蹤路徑的最短距離;ψψ為當前航向角。
其中,半徑RLosRLos的計算公式如式(1)和式(2)所示,為避免RminRmin的計算出現零值,在最終的計算中加入了2倍的船長LppLpp來進行處理[9]。
|
???????????????????????????a(t)=(x(t)?xk)2+(y(t)?yk)2?????????????????????√b(t)=(xk+1?x(t))2+(y(t)?yk+1)2????????????????????????√c(t)=(xk+1?xk)2+(yk+1?yk)2??????????????????????√Rmin(t)=a(t)2?(c(t)2?b(t)2+a(t)22c(t))2???????????????????????????{a(t)=(x(t)?xk)2+(y(t)?yk)2b(t)=(xk+1?x(t))2+(y(t)?yk+1)2c(t)=(xk+1?xk)2+(yk+1?yk)2Rmin(t)=a(t)2?(c(t)2?b(t)2+a(t)22c(t))2 |
(1) |
|
RLos=Rmin(t)+2LppRLos=Rmin(t)+2Lpp |
(2) |
式中,所計算的RminRmin即為當前時刻t的航跡誤差ε,也即圖1中的dd。
圖? 1? LOS導航原理圖
Figure? 1.? Schematic diagram of LOS algorithm
?
船舶在沿著路徑進行跟蹤時,若進入下一個航向點的一定范圍內,即以Pk+2(xk+2,yk+2)Pk+2(xk+2,yk+2)為圓心、RACRAC為半徑的接受圓內,則更新當前航向點為下一航向點,半徑RACRAC一般選取為2倍船長。
1.2?? 基于強化學習的控制過程設計
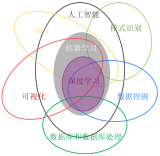
強化學習(reinforcement learning,RL)與深度學習同屬機器學習范疇,是機器學習的一個重要分支,主要用來解決連續決策的問題,是馬爾可夫決策過程(Markov decision processes,MDP)問題[10]的一類重要解決方法。
此類問題均可模型化為MDP問題,簡單表示為四元組。其中,SS為所有狀態值的集合,即狀態空間;AA為動作值集合的動作空間;PP為狀態轉移概率矩陣,即在tt時刻狀態為St=sSt=s的情況下選擇動作值為At=aAt=a,則t+1t+1時刻產生狀態為s1s1的概率Pass1=P[St+1=s1|St=s,At=a]Pss1a=P[St+1=s1|St=s,At=a];R=r(s,a)R=r(s,a)為回報獎勵函數,用于評價在ss狀態下選取動作值aa的好壞。航跡跟蹤控制系統中的控制部分用MDP模型表示如圖2所示。,a,p,r>
圖? 2? 船舶控制的MDP模型
Figure? 2.? MDP model of ship control
?
如圖2所示,船舶智能體直接與當前控制環境進行交互而且不需要提前獲取任何信息。在訓練過程中,船舶采取動作值atat與環境進行交互更新自己的狀態st→st+1st→st+1,并獲得相應的獎勵rt+1rt+1,之后,繼續采取下一動作與環境交互。在此過程中,會產生大量的數據,利用這些數據學習優化自身選擇動作的策略policyππ。簡單而言,這是一個循環迭代的過程。在強化學習中,訓練的目標是找到一個最佳的控制策略 policyπ?π?,以使累積回報值RtRt達到最大[11]。在下面的公式中,γγ為折扣系數,用來衡量未來回報在當前時期的價值比例,設定γ∈[0,1]γ∈[0,1]。
|
Rt=rt+γrt+1+γ2rt+2+?=∑k=1∞γkrt+k+1Rt=rt+γrt+1+γ2rt+2+?=∑k=1∞γkrt+k+1 |
(3) |
Policy?ππ可以使用2種值函數進行評估:狀態值函數Vπ(st)Vπ(st)和動作值函數Qπ(st,at)Qπ(st,at)。其中Vπ(st)Vπ(st)為在遵循當前策略的狀態下對累積回報值的期望,EE為期望值;類似地,Qπ(st,at)Qπ(st,at)表示基于特定狀態和動作情況(st,at)(st,at)下對累積回報值的期望。
|
Vπ(st)=Eπ[Rt|st]=Eπ[∑k=1∞γkrt+k+1|st]Vπ(st)=Eπ[Rt|st]=Eπ[∑k=1∞γkrt+k+1|st] |
(4) |
|
Qπ(st,at)=Eπ[Rt|st,at]=Eπ[∑k=1∞γkrt+k+1|st,at]Qπ(st,at)=Eπ[Rt|st,at]=Eπ[∑k=1∞γkrt+k+1|st,at] |
(5) |
根據值函數和上述最佳控制策略policy?π?π?的定義,最佳policy?π?π?總是滿足以下條件:
|
π?=argmaxVπ(st)=argmaxQπ(st,at)π?=argmaxVπ(st)=argmaxQπ(st,at) |
(6) |
1.3?? 航跡跟蹤問題馬爾可夫建模
從以上描述可以看出,在基于強化學習的控制設計中,馬爾可夫建模過程的組件設計是最為關鍵的過程,狀態空間、動作空間和獎勵的正確性對算法性能和收斂速度的影響很大。所以針對智能船舶的軌跡跟蹤問題,對其進行馬爾可夫建模設計。
1) 狀態空間設計。
根據制導采用的LOS算法,要求當前航向角根據LOS角進行調節以達到跟蹤效果。所以在選取狀態時,需考慮LOS算法中的輸出參數,包括目標航向ψLOSψLOS與實際航向ψψ的差值ee、航跡誤差ε,以及與航跡點距離誤差εdεd。
對于船舶模型,每個時刻都可以獲得當前船舶的縱蕩速度uu、橫蕩速度vv、艏轉向速度rr和舵角δδ。為使強化學習能實現高精度跟蹤效果,快速適應多種環境的變換,除了選取當前時刻的狀態值外,還加入了上一時刻的狀態值進行比較,以及當前航向誤差與上一時刻航向誤差的差值e(k?1)e(k?1),使當前狀態能夠更好地表示船舶是否在往誤差變小的方向運行。最終,當前時刻t的狀態空間可設計為
|
st=[et,εt,εdt,ut,vt,rt,δt,e(k?1)t,et?1,εt?1,εdt?1,ut?1,vt?1,rt?1,δt?1]st=[et,εt,εtd,ut,vt,rt,δt,e(k?1)t,et?1,εt?1,εt?1d,ut?1,vt?1,rt?1,δt?1] |
(7) |
2) 動作空間設計。
針對航跡跟蹤任務特點,以及LOS制導算法的原理,本文將重點研究對船舶航向,即舵角的控制,不考慮對船速與槳速的控制。動作空間只有舵令一個動作值,即δδ,其值的選取需要根據實際船舶的控制要求進行約束,設定為在(?35°,35°)(?35°,35°)以內,最大舵速為15.8 (°)/s。
3) 獎勵函數設計。
本文期望航向角越靠近LOS角獎勵值越高,與目標航跡的誤差越小獎勵值越高。因此,設計的獎勵函數為普遍形式,即分段函數:
|
rt={0,?|e|?0.1|e(k?1)|?0.01|ε|,if|e|?0.1radif|e|>0.1radrt={0,if|e|?0.1rad?|e|?0.1|e(k?1)|?0.01|ε|,if|e|>0.1rad |
(8) |
式中,e(k?1)e(k?1)為當前航向誤差與上一時刻航向誤差的差值。當差值大于0.1rad0.1rad時選擇負值獎勵,也可稱之為懲罰值,是希望訓練網絡能盡快改變當前不佳的狀態。將負值的選取與另一分段的00獎勵值做明顯對比,使其訓練學習后可以更加快速地選擇獎勵值高的動作,從而達到最優效果。
1.4?? 控制系統總體方案
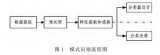
基于強化學習的智能船舶航跡控制系統總體框架如圖3所示。LOS算法根據船舶當前位置計算得到需要的航向以及航跡誤差,在與船舶的狀態信息整合成上述所示狀態向量stst后輸入進航跡控制器中,然后根據強化學習算法輸出當前最優動作值atat給船舶執行,同時通過獎勵函數rtrt計算獲得相應的獎勵來進行自身參數迭代,以使航跡控制器具備自學習能力。
圖? 3? 基于強化學習的智能船舶軌跡跟蹤控制框圖
Figure? 3.? Block diagram of intelligent ship tracking control based on RL
?
在將控制器投入實時控制之前,首先需要對控制器進行離線訓練。設定規定次數的訓練后,將獲得的使累計回報值達到最大的網絡參數進行存儲整合,由此得到強化學習控制器,并應用于航跡跟蹤的實時控制系統。
要解決強化學習問題,目前有許多的算法、機制和網絡結構可供選擇,但這些方法都缺少可擴展的能力,并且僅限于處理低維問題。為此,Mnih等[6]提出了一種可在強化學習問題中使用大規模神經網絡的訓練方法——DQN算法,該算法成功結合了深度學習與強化學習,使強化學習也可以擴展處理一些高維狀態、動作空間下的決策問題[12]。DQN算法可解決因強化學習過程與神經網絡逼近器對值函數逼近的訓練相互干擾,而導致學習結果不穩定甚至是產生分歧的問題[13],是深度強化學習領域的開創者。
DQN算法顯著提高了復雜強化學習問題的穩定性和性能,但因其使用的是離散的動作空間,故需要對輸出的動作進行離散化,且只能從有限的動作值中選擇最佳動作。對于船舶的軌跡跟蹤問題,如果候選動作數量太少,就很難對智能體進行精確控制。為使算法滿足船舶的操縱特性與要求,本文選擇了一種適用于連續動作空間的深度強化學習算法,即基于DDPG的算法[14]來對智能船舶航跡跟蹤控制器進行設計,該算法不僅可以在連續動作空間上進行操作,還可以高效精準地處理大量數據。
2.?? 基于DDPG算法的控制器設計
2.1?? DDPG算法原理
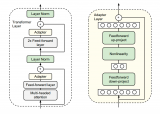
DDPG是Lillicrap等[14]將DQN算法應用于連續動作中而提出的一種基于確定性策略梯度的Actor-Critic框架無模型算法。DDPG的基本框架如圖4所示。
圖? 4? DDPG基本框架
Figure? 4.? Block diagram of DDPG
?
網絡整體采用了Actor-Critic形式,同時具備基于值函數的神經網絡和基于策略梯度的神經網絡:Actor網絡的θπθπ表示確定性策略函數a=π(s|θπ)a=π(s|θπ),Critic網絡的θQθQ表示值函數Q(s,a|θQ)Q(s,a|θQ)。并且DDPG還借鑒了DQN技術,其通過采取經驗池回放機制(experience replay)以及單獨的目標網絡來消除大規模神經網絡帶來的不穩定性。
所謂經驗池回放機制,即在每個時間點都存儲當前狀態、動作等信息作為智能體的經驗et=(st,at,rt,st+1)et=(st,at,rt,st+1),以此形成回放記憶序列D={e1,?,eN}D={e1,?,eN}。在訓練網絡時,從中隨機提取mini batch數量的經驗數據作為訓練樣本,但重復使用歷史數據的操作會增加數據的使用率,也打亂了原始數據的順序,會降低數據之間的關聯性。而目標網絡則建立了2個結構一樣的神經網絡——用于更新神經網絡參數的主網絡和用于產生優化目標值的目標網絡,初始時,將主網絡參數賦予給目標網絡,然后主網絡參數不斷更新,目標網絡不變,經過一段時間后,再將主網絡的參數賦予給目標網絡。此循環操作可使優化目標值在一段時間內穩定不變,從而使得算法性能更加穩定。
在訓練過程中,主網絡中的Actor網絡根據從經驗池中隨機選取的樣本狀態ss,經過當前策略函數a=π(s|θπ)a=π(s|θπ)選擇出最優的動作值aa交予船舶智能體,讓其與環境交互后得到下一時刻的狀態值s′s′。而此時的Critic網絡則接受當前的狀態ss和動作值aa,使用值函數Q(s,a|θQ)Q(s,a|θQ)評價當前狀態的期望累計獎賞,并用于更新Actor網絡的參數。在目標網絡中,整體接收下一時刻的狀態s′s′,經目標Actor網絡選出動作后交予目標Critic獲得目標期望值Q′(a′)Q′(a′),然后,再通過計算損失函數對主網絡的Critic網絡參數進行更新。對于主網絡的Actor網絡參數更新,Silver等[15]證實,確定性策略的目標函數J(θπ)J(θπ)采用ππ策略的梯度與Q函數采用ππ策略的期望梯度是等價的:
|
?J(θπ)?θπ=Es[?Q(s,a|θQ)?θπ]?J(θπ)?θπ=Es[?Q(s,a|θQ)?θπ] |
(9) |
根據確定性策略a=π(s|θπ)a=π(s|θπ),得到Actor網絡的梯度為:
|
?J(θπ)?θπ=Es[?Q(s,a|θQ)?a?π(s|θπ)?θπ]?J(θπ)?θπ=Es[?Q(s,a|θQ)?a?π(s|θπ)?θπ] |
(10) |
|
?θπJ≈1N∑i(?aQ(s,a|θπ)|s=si,a=π(si)??θππ(s|θπ)|s=si)?θπJ≈1N∑i(?aQ(s,a|θπ)|s=si,a=π(si)??θππ(s|θπ)|s=si) |
(11) |
另一方面,對于Critic網絡中的價值梯度:
|
?L(θQ)?θQ=Es,a,r,s′~D[(TargetQ?Q(s,a|θQ))?Q(s,a|θQ)?θQ]?L(θQ)?θQ=Es,a,r,s′~D[(TargetQ?Q(s,a|θQ))?Q(s,a|θQ)?θQ] |
(12) |
|
TargetQ=r+γQ′(s′,π(s′|θπ′)|θQ′)TargetQ=r+γQ′(s′,π(s′|θπ′)|θQ′) |
(13) |
式中,θπ′θπ′和θQ′θQ′分別為目標策略網絡和目標值函數網絡的網絡參數。其中,目標網絡的更新方法與DQN算法中的不同,在DDPG算法中,Actor-Critic網絡各自的目標網絡參數是通過緩慢的變換方式更新,也叫軟更新。以此方式進一步增加學習過程的穩定性:
|
θQ′=τθQ+(1?τ)θQ′θQ′=τθQ+(1?τ)θQ′ |
(14) |
|
θπ′=τθπ+(1?τ)θπ′θπ′=τθπ+(1?τ)θπ′ |
(15) |
式中,ττ為學習率。
定義最小化損失函數來更新Critic網絡參數,其中,yiyi為當前時刻狀態動作估計值函數與目標網絡得到的目標期望值間的誤差:
|
L=1N∑i(yi?Q(si,ai|θQ))2L=1N∑i(yi?Q(si,ai|θQ))2 |
(16) |
2.2?? 算法實現步驟
初始化Actor-Critic網絡的參數,將當前網絡的參數賦予對應的目標網絡;設置經驗池容量為30 000個,軟更新學習率為0.01,累計折扣系數設定為0.9,初始化經驗池。訓練的每回合步驟如下:
1) 初始化船舶環境;
2) 重復以下步驟直至到達設置的最大步長;
3) 在主網絡中,Actor網絡獲取此刻船舶的狀態信息stst,并根據當前的策略選取動作舵令δtδt給船舶執行,即δt=π(st|θπ)δt=π(st|θπ);
4) 船舶執行當前舵令后輸出獎勵rtrt和下一個狀態st+1st+1,Actor網絡再次獲取該狀態信息并選取下一舵令δt+1δt+1;
5) 將此過程中產生的數據(st,δt,rt,st+1)(st,δt,rt,st+1)存儲在經驗池中,以作為網絡訓練學習的數據集。當經驗池存儲滿后,再從第1個位置循環存儲;
6) 從經驗池中隨機采樣N個樣本(st,δt,rt,st+1)(st,δt,rt,st+1),作為當前Actor網絡和Critic網絡的訓練數據;
7) 通過損失函數更新Critic網絡,根據Actor網絡的策略梯度更新當前Actor網絡,然后再對目標網絡進行相應的軟更新。
3.?? 系統仿真與算法對比分析
3.1?? 仿真環境構建
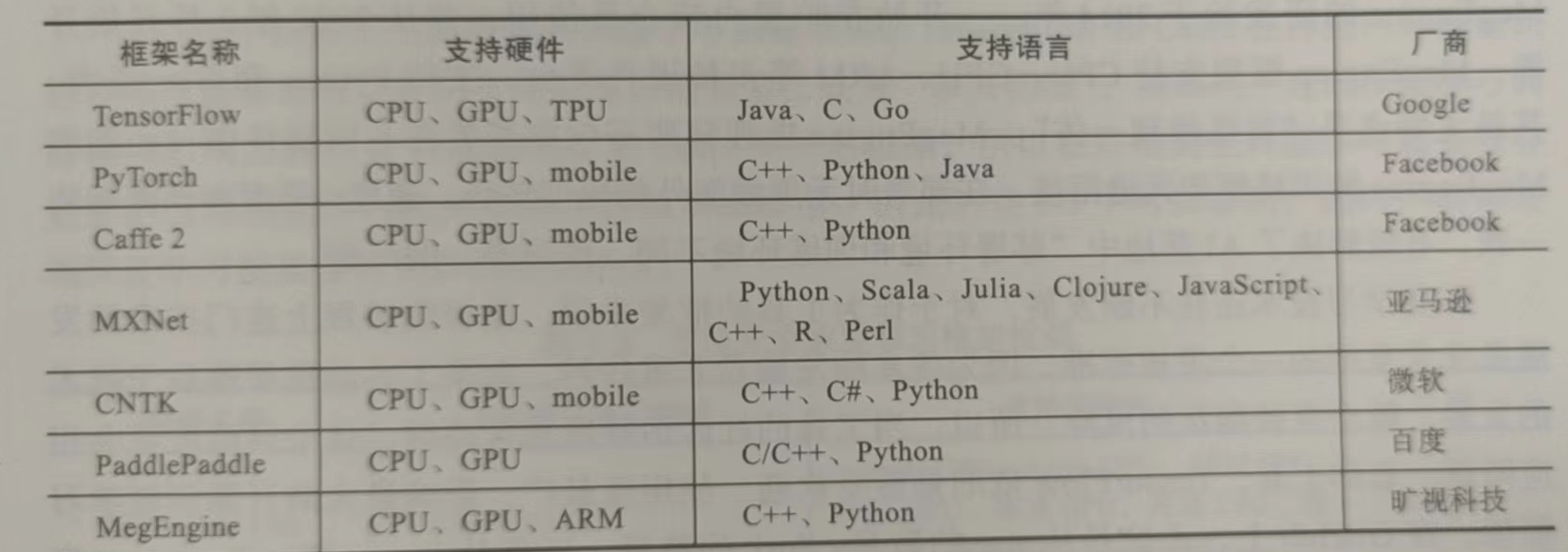
為驗證上述方法的有效性,基于Python環境進行了船舶航跡跟蹤仿真實現。控制研究對象模型選用文獻[16-17]中的單槳單舵7 m KVLCC2船模,建模采用三自由度模型(即縱蕩、橫蕩和艏搖),具體建模過程參考文獻[16]。表1列出了船舶的一些主要參數。
表? 1? KVLCC2船舶參數
Table? 1.? Parameters of a KVLCC2 tanker
| 參數 | 數值 | ? | 參數 | 數值 |
|---|---|---|---|---|
| 船長Lpp/m | 7 | ? | 方形系數CbCb | 0.809 8 |
| 船寬Bwl/m | 1.168 8 | ? | 浮心坐標/m | 0.244 0 |
| 型深D/m | 0.656 3 | ? | 螺旋槳直徑Dp/m | 0.216 0 |
| 排水體積/m3 | 3.272 4 | ? | 舵面積/m2 | 0.053 9 |
|?顯示表格
?
在所選用的DDPG控制器中,Crtic網絡和Actor網絡的實現參數設置分別如表2和表3所示。
表? 2? Critic網絡參數
Table? 2.? Critic network parameters
| 參數 | 賦值 |
|---|---|
| 輸入層 | 狀態向量S(t)S(t) |
| 第1個隱層 | 300 |
| 第1層激活函數 | Relu |
| 第2個隱層 | 200 |
| 第2層激活函數 | Relu |
| 輸出層 | 動作δ(t)δ(t) |
| 輸出層激活函數 | Tanh |
| 參數初始化 | Xavier初始化 |
| 學習率 | 0.000 1 |
| 優化器 | Adam |
?
?
表? 3? Actor網絡參數
Table? 3.? Actor network parameters
| 參數 | 賦值 |
|---|---|
| 輸入層 | 狀態向量S(t)S(t),動作δ(t)δ(t) |
| 第1個隱層 | 300 |
| 第1層激活函數 | Relu |
| 第2個隱層 | 200 |
| 第2層激活函數 | Relu |
| 輸出層 |
Q(S(i),δ(i))Q(S(i),δ(i)) |
| 輸出層激活函數 | Linear |
| 參數初始化 | Xavier初始化 |
| 學習率 | 0.001 |
| 優化器 | Adam |
?
3.2?? 控制器離線學習
基于DDPG算法進行的離線訓練學習設置如下:初始化網絡參數以及經驗緩存池,設計最大的訓練回合為2 000,每回合最大步長為500,采樣時間為1 s。在規劃訓練期間所需跟蹤的航跡時,為使控制器適應多種環境,以及考慮到LOS制導算法中對于航向控制的要求,依據文獻[18]中的設計思想,根據拐角的變換,設計了多條三航跡點航線,每回合訓練時隨機選取一條進行航跡跟蹤。
訓練時,將數據存入經驗池中,然后再從中隨機采樣一組數據進行訓練,狀態值及動作值均進行歸一化處理,當達到最大步長或最終航跡點輸出完成時,便停止這一回合,并計算當前回合的總回報獎勵。當訓練進行到200,300和500回合時,其航向誤差如圖5所示。由圖中可以看出,在訓練時隨著回合的增加,航向誤差顯著減小,控制算法不斷收斂;當訓練達到最大回合結束后,總獎勵值是不斷增加的。為使圖像顯示得更加清晰,截取了200~500回合的總回報獎勵如圖6所示。從中可以看出,在約270回合時算法基本收斂,展現了快速學習的過程。
圖? 5? 航向誤差曲線
Figure? 5.? Course error curves
?
圖? 6? 總回報獎勵曲線
Figure? 6.? Total reward curve
?
3.3?? 仿真實驗設計及對比分析
上述訓練完成后,DDPG控制器保存回報獎勵函數最大的網絡參數,并將其應用于航跡跟蹤仿真。為了驗證DDPG控制器的可行性,本文選用BP-PID控制器進行對比分析。
用于對比的BP-PID控制器選擇使用輸入層節點數為4、隱含層節點數為5、輸出層節點數為3的BP神經網絡對PID的3種參數進行選擇,其中學習率為0.546,動量因子為0.79,并參考文獻[19],利用附加慣性項對神經網絡進行優化。在相同的環境下,將DDPG控制器與BP-PID控制器進行仿真對比分析。仿真時,船舶的初始狀態為從原點(0,0)出發,初始航向為45°,初始航速也即縱蕩速度uu=1.179 m/s,螺旋槳初始速度rr=10.4 r/s。
仿真實驗1:分別設計直線軌跡和鋸齒狀軌跡,用以觀察2種控制器對直線的跟蹤效果和面對劇烈轉角變化時的跟蹤效果(圖7),軌跡點坐標分別為(0,50),(400,50)和(0,0),(100,250),(200,0),(300,250),(400,0),(500,250),(600,0),單位均為m。
?
圖? 7? 航跡跟蹤效果(實驗1)
?
Figure? 7.? Tracking control result (experiment 1)
?
通過對2種類型軌跡跟蹤的對比可以看出,對于直線軌跡,DDPG控制器能夠更加快速地進行穩定跟蹤,在鋸齒狀軌跡轉角跟蹤時其效果也明顯優于BP-PID控制器。對仿真過程中航向角的均方根誤差(圖7(b))進行計算,顯示BP-PID控制器的數值達61.017 8,而DDPG控制器的僅為10.018,后者具有更加優秀的控制性能。
仿真實驗2:為模擬傳統船舶的航行軌跡,設計軌跡點為(0,0),(100,50),(150,250),(400,250),(450,50),(550,0)的航跡進行跟蹤。跟蹤效果曲線和航向均方根誤差(RMSE)的對比分別如圖8和表4所示。
圖? 8? 航跡跟蹤結果(實驗2)
Figure? 8.? Tracking control result (experiment 2)
?
表? 4? 控制性能指標
Table? 4.? Control performance
| 控制器 | RMSE |
|---|---|
| BP-PID控制器 | 13.585 0 |
| DDPG控制器 | 6.911 96 |
?
在此次仿真過程中,進一步對比了2種控制器對于LOS角跟蹤的效果以及舵角的變化頻率,結果分別如圖9和圖10所示。PID經過BP神經網絡參數整定后整體巡航時間約為1 000 s,而DDPG控制器的巡航時間則在此基礎上縮短了4%;在轉角處的航向跟蹤中,DDPG控制器在20 s內達到期望值,而BP-PID的調節時間則約為60 s,且控制效果并不穩定,舵角振動頻率高。由此可見,深度強化學習控制器可以很快地根據航跡變化做出調整,減少了不必要的控制環節,調節時間短,控制效果穩定,舵角變化頻率小,具有良好的控制性能。
?
圖? 9? BP-PID控制器控制效果
?
Figure? 9.? Control result of BP-PID
?
?
圖? 10? DDPG控制器控制效果
Figure? 10.? Control result of DDPG
4.?? 結 語
本文針對船舶的航跡跟蹤問題,提出了一種基于深度強化學習的航跡跟蹤控制器設計思路。首先根據LOS算法制導,建立了航跡跟蹤控制的馬爾可夫模型,給出了基于DDPG控制器算法的程序實現;然后在Python環境中完成了船舶航跡跟蹤控制系統仿真實驗,并與BP-PID控制器進行了性能對比分析。
將航跡跟蹤問題進行馬爾可夫建模設計后,將控制器投入離線學習。通過對此過程的分析發現,DDPG控制器在訓練中能快速收斂達到控制要求,證明了設計的狀態、動作空間以及獎勵函數的可行性。并且航跡跟蹤仿真對比結果也顯示,DDPG控制器能較快地應對航跡變化,控制效果穩定且舵角變化少,對于不同的軌跡要求適應性均相對良好。整體而言,基于深度強化學習的控制方法可以應用到船舶的航跡跟蹤控制之中,在具有自適應穩定控制能力的情況下,不僅免去了復雜的控制計算,也保證了實時性,對船舶的智能控制具有一定的參考價值。
?關注微信公眾號:人工智能技術與咨詢。了解更多咨詢!
編輯:fqj
 電子發燒友App
電子發燒友App



















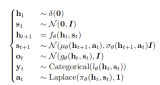
























評論