一、卡諾圖概念

　　卡諾圖是邏輯函數(shù)的一種圖形表示。一個邏輯函數(shù)的卡諾圖就是將此函數(shù)的最小項表達式中的各最小項相應地填入一個方格圖內，此方格圖稱為卡諾圖。卡諾圖的構造特點使卡諾圖具有一個重要性質：可以從圖形上直觀地找出相鄰最小項。兩個相鄰最小項可以合并為一個與項并消去一個變量。

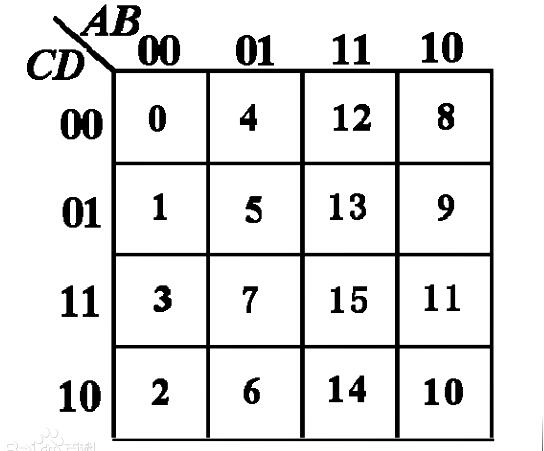
　　二、卡諾圖結構特點

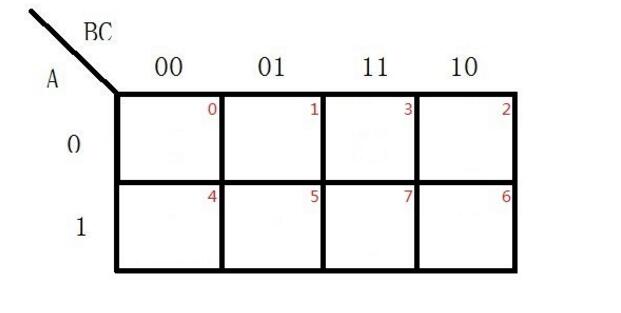
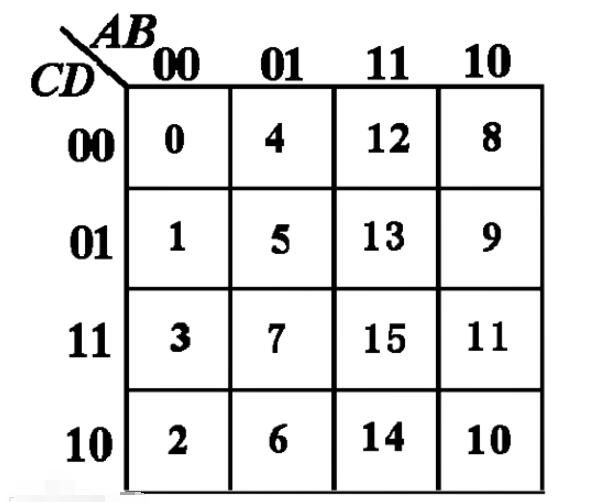
　　卡諾圖中最小項的排列方案不是唯一的，變量的坐標值0表示相應變量的反變量，1表示相應變量的原變量，變量的取值變化規(guī)律按“循環(huán)碼”變化［1］。各小方格依變量順序取坐標值，所得二進制數(shù)對應的十進制數(shù)即相應最小項的下標i。

　　在五變量卡諾圖中，為了方便省略了符號“m”，直接標出m的下標i。

　　歸納起來，卡諾圖在構造上具有以下兩個特點：

　　☆n個變量的卡諾圖由2^n個小方格組成，每個小方格代表一個最小項；

　　☆卡諾圖上處在相鄰、相對、相重位置的小方格所代表的最小項為相鄰最小項。

　　可以從圖形上直觀地找出相鄰最小項。兩個相鄰最小項可以合并為一個與項并消去一個變量。

　　三、卡諾圖的性質

　　卡諾圖的構造特點使卡諾圖具有一個重要性質：可以從圖形上直觀地找出相鄰最小項合并。合并的理論依據(jù)是并項定理AB+AB=A。例如，

　　根據(jù)定理AB+AB=A和相鄰最小項的定義，兩個相鄰最小項可以合并為一個與項并消去一個變量。例如，4變量最小項ABCD和ABCD相鄰，可以合并為ABD；ABCD和ABCD相鄰，可以合并為ABD；而與項ABD和ABD又為相鄰與項，故按同樣道理可進一步將兩個相鄰與項合并為BD。

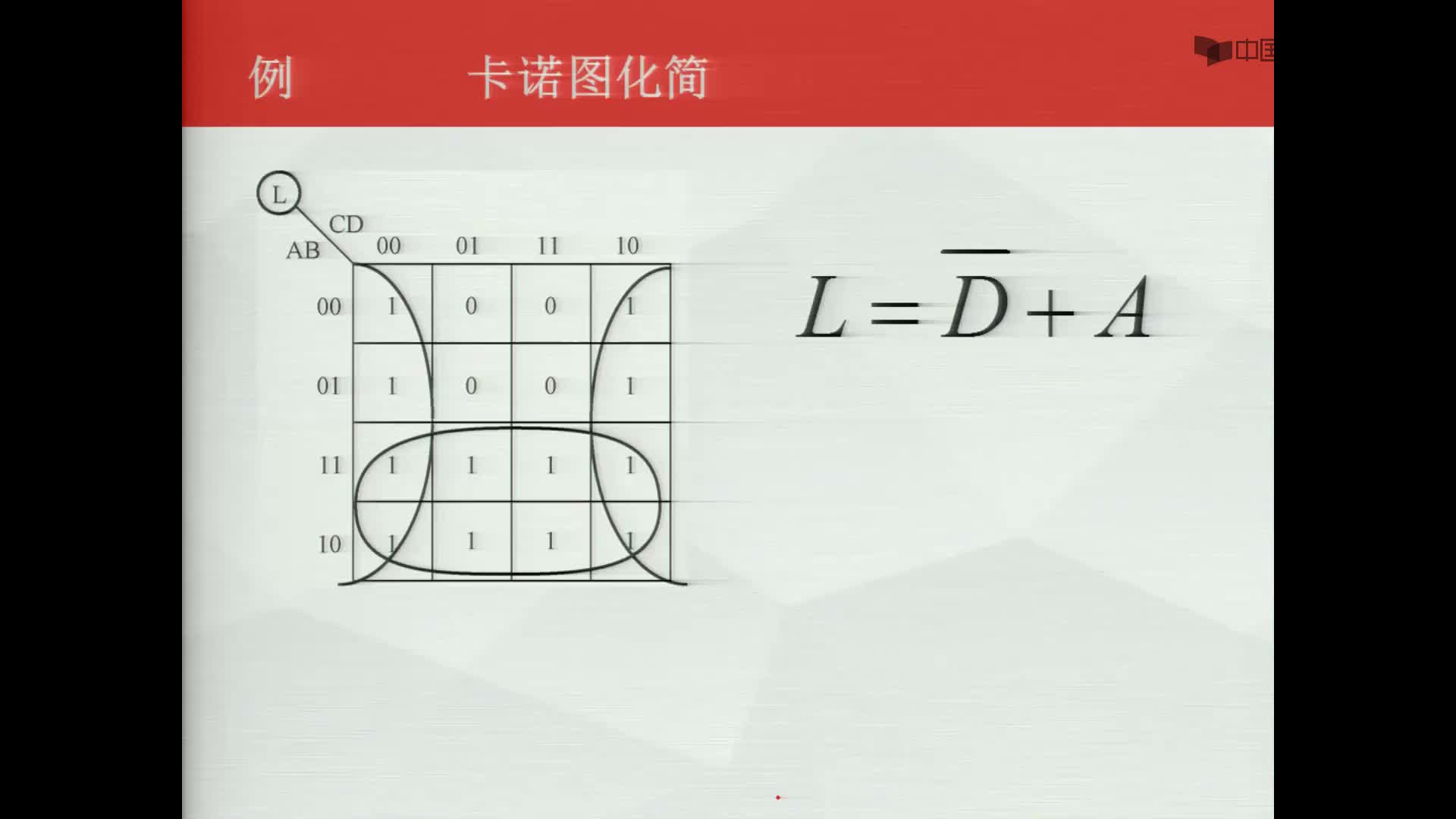
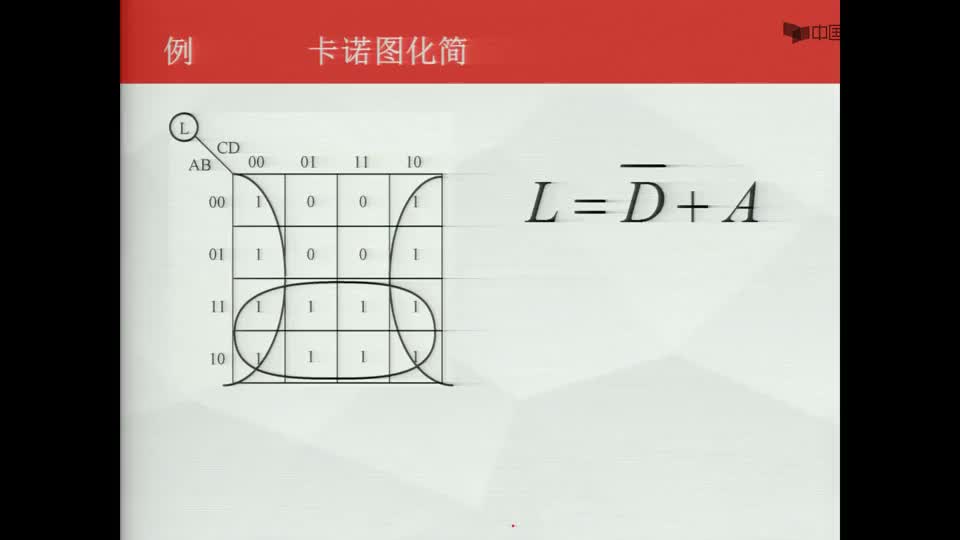
　　用卡諾圖化簡邏輯函數(shù)的基本原理就是把上述邏輯依據(jù)和圖形特征結合起來，通過把卡諾圖上表征相鄰最小項的相鄰小方格“圈”在一起進行合并，達到用一個簡單“與”項代替若干最小項的目的。

　　通常把用來包圍那些能由一個簡單“與”項代替的若干最小項的“圈”稱為卡諾圈。

　　邏輯函數(shù)在卡諾圖上的表示

　　1．給定邏輯函數(shù)為標準“與-或”表達式

　　當邏輯函數(shù)為標準“與-或”表達式時，只需在卡諾圖上找出和表達式中最小項對應的小方格填上1，其余小方格填上0，即可得到該函數(shù)的卡諾圖。

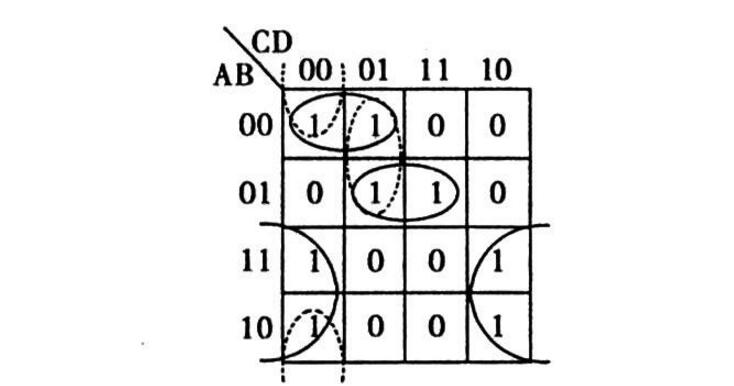
　　例如，3變量函數(shù)F（A，B，C）=∑m（1，2，3，7）的卡諾圖如圖2．6所示。

　　圖2．6函數(shù)F（A，B，C）=∑m（1，2，3，7）的卡諾圖

　　2．邏輯函數(shù)為一般“與-或”表達式

　　當邏輯函數(shù)為一般“與-或”表達式時，可根據(jù)“與”的公共性和“或”的疊加性作出相應卡諾圖。

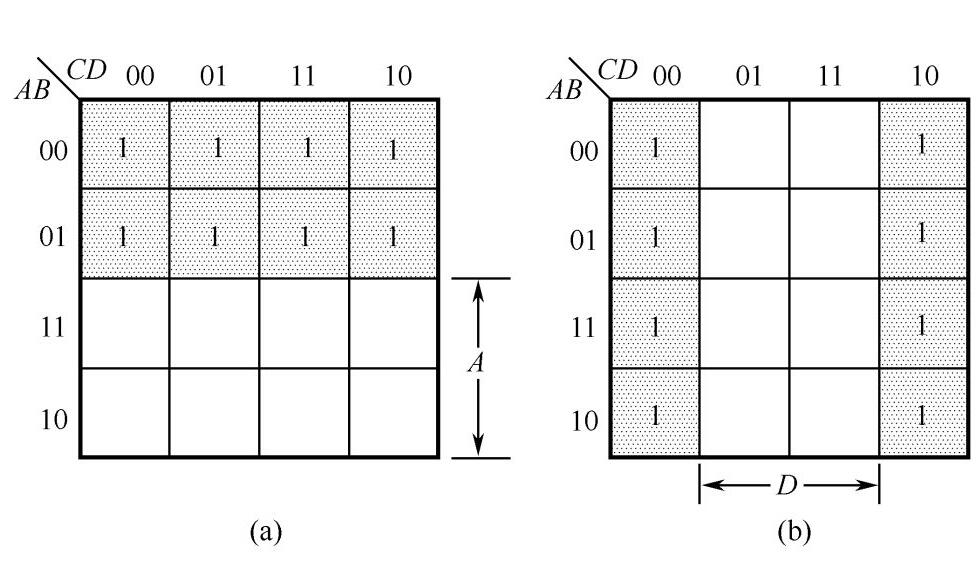
　　例如，4變量函數(shù)F（A，B，C，D）=AB+CD+A·BC的卡諾圖如圖2．7所示。

　　圖2．7函數(shù)F（A，B，C，D）=AB+CD+A·BC的卡諾圖

　　填寫該函數(shù)卡諾圖時，只需在4變量卡諾圖上依次找出和“與項”AB、CD、A·BC對應的小方格填上1，便可得到該函數(shù)的卡諾圖。

　　當邏輯函數(shù)表達式為其他形式時，可將其變換成上述形式后再作卡諾圖。

　　為了敘述的方便，通常將卡諾圖上填1的小方格稱為1方格，填0的小方格稱為0方格。0方格有時用空格表示。