這篇文章分為三個部分,解讀某個學生在EDN姐妹媒體EEWeb論壇上所提出的一個問題,其核心如下:他的老師布置了一個布爾方程式;然后要求他創(chuàng)建相應的真值表;然后再告訴他要進行卡諾圖化簡;最后要他必須只使用與非(NAND)門或只使用或非(NOR)門來實現(xiàn)這個電路。
因此,一開始要做的就是考慮為什么首先要提出這種問題。接下來就是更詳細地研究這個學生的特定問題,并將其轉換成最初的與或解決方案。然后,就是考慮將與或電路轉換為與非-或非對應電路的一般概念。最后,就是用所學的知識來解決這個學生的最初問題。
為什么要只使用與非門或只使用或非門?
那么,為什么老師都會要求他的學生只使用與非門或只使用或非門來實現(xiàn)邏輯函數(shù)?(請注意,我特地不說“只使用與非門或或非門”,因為這有可能被理解成可以使用與非門和或非門,而不使用與門和或門。)
盡管學生可能對此感到驚訝,但不一定就說明老師是個不成功的人,他生活中唯一的樂趣就是去折磨學生。話雖這么說,但回想起我自己還是一名學生的日子,我們最好不要實際排除這種可能的動機。
我不由自主地想到老師給學生布置這個作業(yè)可能有以下原因:
1.給出一個用與門或或門(乘積的和或和的乘積形式)描述的電路,然后要求學生將其轉換成只使用與非門、只使用或非門或使用與非門和或非門組合的另一種表現(xiàn)形式,是確保讓學生了解各種邏輯門如何工作的好方法。它還有助于確保讓學生了解德·摩根變換之類的內容。
2.如果你想使用簡單的邏輯器件——例如包含六個非門或四個2輸入與門、或門、與非門或或非門的雙列直插(DIL)封裝集成電路(IC)——來設計印制電路板(PCB),而你可能正好沒有與門之類的東西,但是碰巧有一個與非門和一個非門備用(或者可能是一個或門和三個非門),那么在這種情況下,你對邏輯門的理解就可能扭轉局面。
3.最簡單的邏輯門是非門。假設是CMOS電路,那么一個非門需要兩個晶體管。與非門和或非門要復雜一些,這兩種門每種包含四個晶體管。然后是與門和或門,這兩種門每種包含六個晶體管。也就是說,如果使用與非門或或非門代替與門或或門,那么所使用的晶體管數(shù)量可以減少三分之一。
4.關于上一點,與門實際上是由一個與非門后接一個非門構成的(同樣,或門是由一個或非門后接一個非門所組成)。除了使用4+2=6個晶體管外,這還說明與門(和或門)具有兩級延遲。因此,如果可以使用與非門取代與門(或用或非門取代或門),所得到的電路會運行得更快。
5.順便稍微說一句,本文所討論的所有內容在我的書“Bebop to the Boolean Boogie”中都有詳細描述。
實際上,現(xiàn)在已很少有人在門級進行設計。取而代之的是以較高層級的抽象捕獲設計,然后使用邏輯綜合引擎生成相應的門級等效設計。這說明上述第2點到第4點不再像以前那樣重要。
你可以爭辯說,第1點也是如此,但我不太同意。我的想法是,它類似于使用計算器進行計算的概念。如果你有一個計算器,那你實際上就不需要知道如何對整數(shù)、實數(shù)和浮點數(shù)進行加減乘除運算,但是,如果你掌握了這類知識,那么當你計算器的電池沒電時,它就可以派上用場。同樣,盡管你可能不需要每天處理布爾結構,但是在需要時知道如何處理就會非常方便。
思考問題
所以,下面是那個學生給我的。他首先說,老師向班級展示了以下方程式:
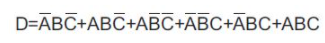
那個學生還告訴我,他已經使用這個方程式生成了下面的真值表,但是從這時起,他遇到了麻煩而做不下去了。
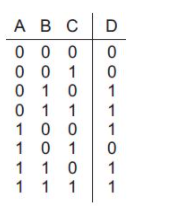
好吧,我不得不告訴他,我對他遇到的問題一點都不感到驚訝,因為在他的方程式里有六個乘積項,每個乘積項在他的真值表的輸出列中都應該有一個對應的1,但是實際上,他的真值表的輸出列中只有五個1。
我對這個情況進行了反復考慮,我認為潛在的問題是他缺乏對基本原理的理解。還有一點是,如果有一個學生感到困惑,那么就很可能不止他一個人。最后但同樣重要的是,我記得我剛開始時有點困惑不解,所以我會花一點時間逐步解決這個問題(如果你感到無聊,請隨時跳過;或者,你也可以隨時試著發(fā)現(xiàn)我可能引入的任何故意的錯誤,以便了解你是否有集中精力)。
我要做的第一件事就是在方程式中對乘積項進行編號,以便可以對我們所處的位置和所做的事進行跟蹤(如果我們是來真的,那么就不必費心對乘積項進行編號):
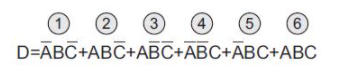
下一步是創(chuàng)建真值表。可以從以標準二進制數(shù)表示的所有輸入組合開始,如下面的(a)所示;然后將與六個乘積項相對應的六個1加起來,如(b)到(g)所示;最后把任何剩余的輸出“位置”都填入0,如下面的(h)所示。
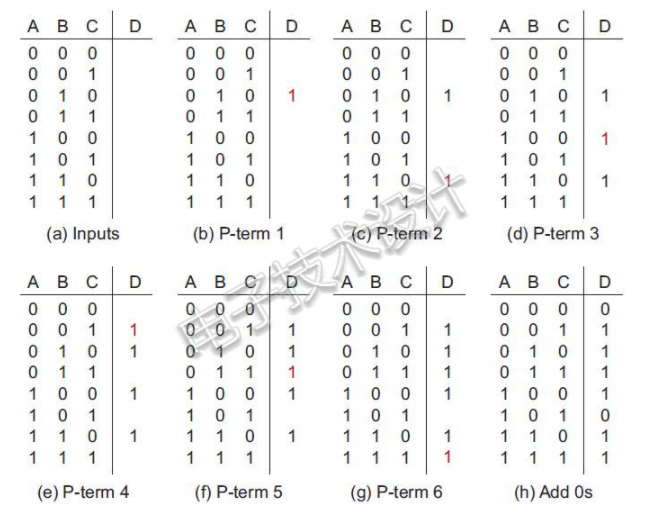
這里要注意的重點是,將方程式轉換為真值表確實一點也不困難。話雖如此,但無論誰這樣做,都必須了解這個過程背后的基本邏輯。再看一下這個方程式,其本質可以這樣來表達:“如果第一個乘積項(第一個與函數(shù))為真,則輸出為真(邏輯1),或者如果第二乘積項為真,則輸出為真,或者如果第三乘積項為真……)。這就是為什么可以在與每個乘積項相對應的輸出列中簡單地填寫1——如果這些乘積項中的任何一項為真,則輸出為真(1),否則輸出為假(0)。
下一步是創(chuàng)建卡諾圖。首先是創(chuàng)建網格本身。由于總共有三個輸入,因此可以使用兩種方法(方案)來做這一步,如下所示:
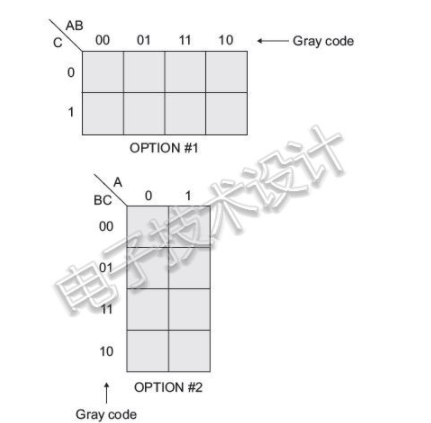
選擇使用哪種方案都沒有關系。這兩種情況下答案都是相同的(如果不是,那就確實有問題)。這里使用方案1,這種方法我比較喜歡。如果有任何學生正在閱讀本文,我建議你在這步完成后從此處開始,自己使用卡諾圖方案2進行重做,以便確保你真正了解這個過程。
查看卡諾圖方案1,觀察“AB”所處的位置。右側是與AB輸入相關的0和1的四種組合:“00”、“01”、“11”和“10”。請務必注意,這四種組合是以格雷碼形式進行排列,這樣就可以讓我們從一個值移到相鄰值時,只會有一位發(fā)生變化。這是卡諾圖運作的關鍵。

在二進制代碼中,當從01過渡到10時,會有兩位發(fā)生變化。相比之下,如果查看格雷碼(01至11)中的相應轉換,則只有一位發(fā)生變化。
此外,請注意二進制代碼的最后一行。如果要從這一行轉而過渡到第一行(11到00),那么就會再次有兩位發(fā)生變化。但是,如果查看格雷碼中的相應行(10到00),則會再次看到只有一位發(fā)生變化。
好了,現(xiàn)在來填充卡諾圖。這一步是向方程式中的乘積項所對應的每個方框中填入1。這里再次按照下面的步驟逐步填寫(圓圈中的小數(shù)字1到6與初始方程式中的乘積項相對應):
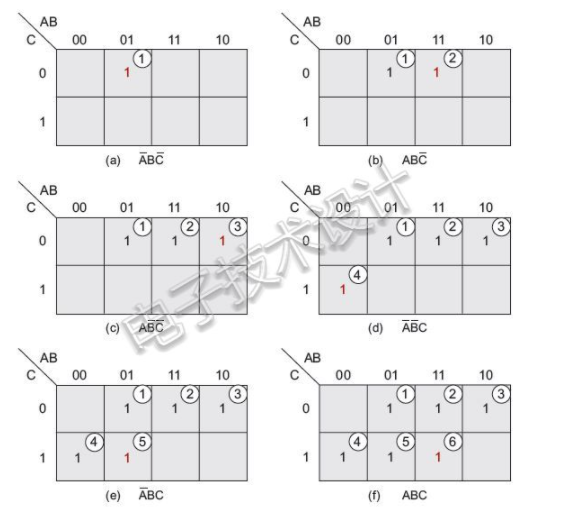
這里需要注意的另一點是,不需要真值表即可填充卡諾圖。這里要做的只是沿著方程式一項一項來,對每個乘積項在對應的卡諾圖“方框”中填入1。
下一步是使用卡諾圖來化簡邏輯表達式。從上面的最終卡諾圖(f)可以立即看出,可以將其簡化為三個項。像往常一樣,我們一次一次地完成每一步。
觀察下圖中用紅色圈出的兩個1,我們知道,這兩種情況下的輸出均為1。對于這兩個框中的每個框都有A=0,C=1,因此這兩個值很重要。但是,這兩個框中有一個是B=0,另一個則是B=1。這就是說,只要A=0,C=1,那么我們就不在乎B是0還是1。
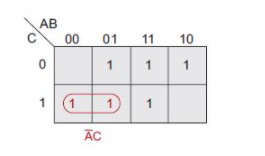
接下來看一下下圖中用紅色圈出的第二組兩個1。對于這兩個框中的每個框都有A=1,C=0,因此這兩個值很重要。但是,這兩個框中也是有一個是B=0,另一個是B=1。這就是說,只要A=1,C=0,那么我們就不在乎B是0還是1。
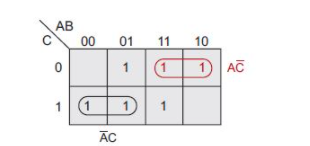
最后但同樣重要的是,下面來看一下下圖中用紅色圈出的一組四個1(卡諾圖的技巧之一是可以將相同的1用作多個組的一部分)。
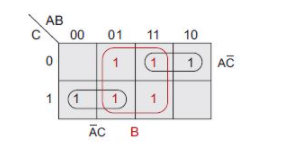
在這種情況下,這四個框中有兩個框是A=0,另外兩個框則是A=1,這就是說我們不在乎A是0還是1。類似地,這四個框中有兩個框是C=0,另外兩個框是C=1,因此我們就不在乎C是0還是1。實際上,對于所有這四個框而言,唯一恒定的輸入是B,它始終為1。
這樣,就可以使用卡諾圖最簡表達式來編寫優(yōu)化的乘積和方程,如下所示:
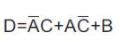
由此就可以使用非門、與門和或門輕松繪制相應的門級原理圖,如下所示:
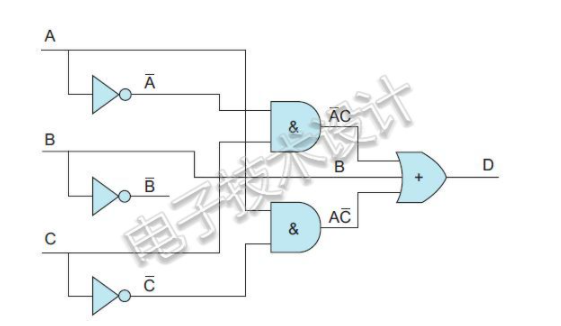
至此,我知道你會跟我說我們沒有使用!B信號(這里使用“!”字符來表示非B,因為在文本里在字母上畫一條橫線有點難),但我們將在不久的將來使用它。說到這,未來比你想象的要近。這是我們必須考慮的重點,因為那位令人討厭的老師他所布置的作業(yè)是只使用與非門或或非門來展示最終電路。
使用與非門或或非門實現(xiàn)非門
讓我們從容易的開始,先解決本例中的三個非門。首先我們先回憶一下,五種常見基本門的真值表如下所示:
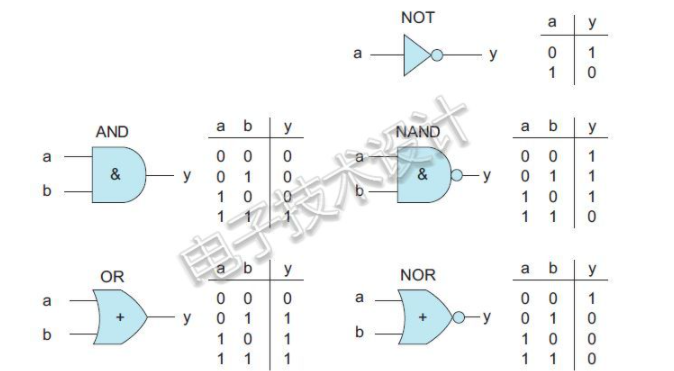
也就是說,如果將與非門的輸入捆綁(連接)在一起,那么得到的功能就是非門。如果將或非門的輸入捆綁在一起,那么得到的結果也相同。也就是說,以下功能相同:

對與門、或門、與非門和或非門進行德·摩根變換
奧古斯都·德·摩根(Augustus DeMorgan,1806至1871年)是喬治·布爾(George Boole)的同齡人。他在符號邏輯領域做出了重大貢獻,尤其是我們現(xiàn)在在用的一組規(guī)則——德·摩根變換。
為了對布爾表達式進行德·摩根變換,需要按以下步驟進行:
1.將所有的與運算符換成或運算符,反之亦然。
2.將所有的輸入變量反轉,也可將任何0換成1,反之亦然。
3.將整個函數(shù)反轉。
4.減少任何多次反轉。
一般而言,我們傾向于對多項式進行德·摩根變換,但是也可以對單個門進行變換,這樣就得到以下結論:
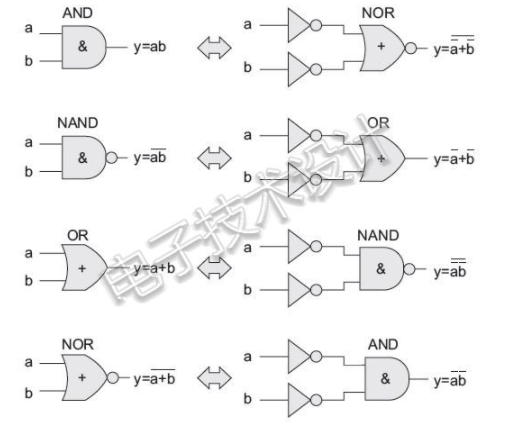
我不了解你,所以沒辦法解釋,但是在查看了上面的德·摩根變換后,我感覺很滿意,并且感覺在(邏輯)世界中一切都是對的。
只使用與非門來表示電路
老實說,現(xiàn)在我們已奠定了基礎,這個部分非常容易。讓我們回憶下,使用非門、與門和或門實現(xiàn)的電路是什么樣的:
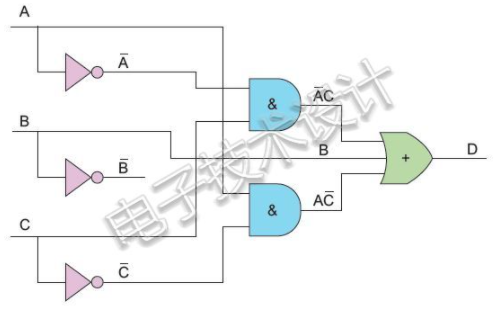
我對它們進行了顏色編碼,以便讓我們清楚了解自己在做什么。下面就來做出決定,我們只希望使用與非門。因此,使用前面討論的所有內容,就可以將非門、或門和與門換成與非門。
和往常一樣,我們一步步來做。首先從左邊用粉紅色表示的三個非門開始。我們知道,可以將這三個門中的每一個換成一個2輸入與非門(它們的輸入是捆綁在一起),所以這里沒有問題。

接下來來研究電路右側用綠色表示的3輸入或門。根據(jù)德·摩根變換,我們知道,可以用一個3輸入與非門(其輸入帶有非門)來代替它,如下所示。
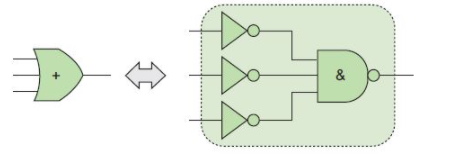
當然,可以將這三個非門中的每一個再次用一個2輸入與非門來替換,如下所示:
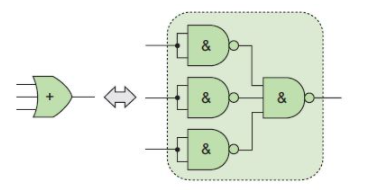
因此,現(xiàn)在只需要考慮電路中間兩個用藍色表示的與門了。當然,德·摩根變換在這里幫不上忙,因為與門的等效電路是將或非門的所有輸入都加上非門,但這個作業(yè)不允許我們使用或非門。
有時,我們傾向于使事情變得比所需要的更復雜。在這種情況下,要做的就是記住,與門實際上是由與非門后接一個非門形成的(同樣,或門是由或非門后接一個非門所組成)。也就是說,可以像下面這樣來替換與門:
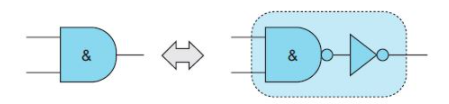
當然,由于作業(yè)要求只使用與非門,因此必須將非門替換成其等效的2輸入與非門,如下所示:
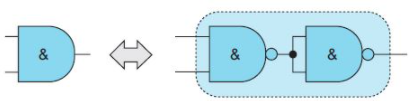
現(xiàn)在,萬事大吉了。因此,如果把上述所有變換結合起來,那么只使用與非門的實現(xiàn)就如下所示:
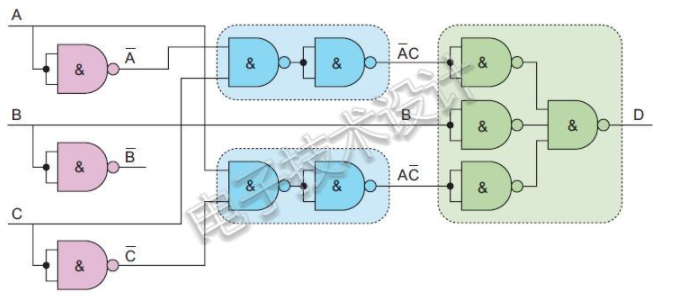
雖然上面的電路可以執(zhí)行所需的功能,但是這里有幾個門浪費了,因為如下面用紅色框框出的部分所示,有兩個地方出現(xiàn)了非門接非門的情況(當然都是用與非門來實現(xiàn)):
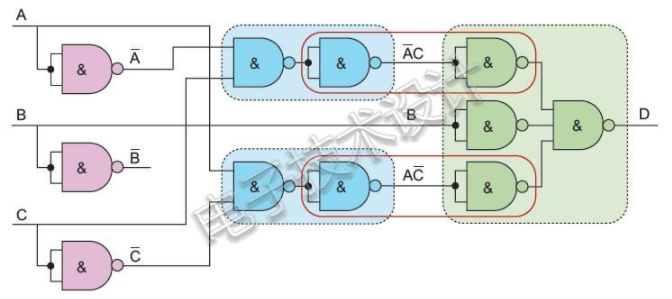
每當以非函數(shù)形式出現(xiàn)偶數(shù)次反轉時,都可以用一條簡單的線來代替它們。因此,稍作修改就得到如下所示的最終電路:
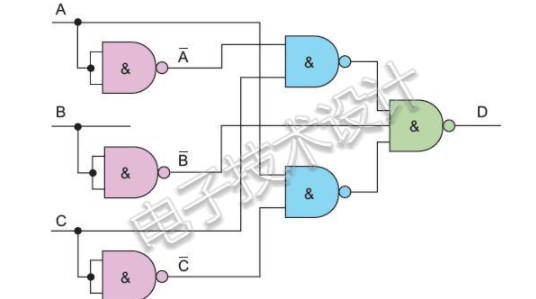
如果非門、與非門和或非門分別等于一級延遲,與門和或門分別等于兩級延遲,那么在最初的非門、與門和或門電路實現(xiàn)中,最壞情況的輸入到輸出路徑就等于1+2+2=5級延遲。相比之下,經過優(yōu)化的只使用與非門的實現(xiàn)則僅會發(fā)生最多1+1+1=3級延遲。
再說一次,如果有任何學生正在閱讀本文,只是為了確保你100%掌握以上所有內容,建議你以以上討論為基礎創(chuàng)建只使用或非門的實現(xiàn)。在此期間,歡迎提出任何意見和問題,也希望能有更多有經驗的讀者愿意分享任何相關的提示與技巧。
編輯:hfy
-
NAND
+關注
關注
16文章
1690瀏覽量
136356 -
晶體管
+關注
關注
77文章
9744瀏覽量
138709 -
非門
+關注
關注
1文章
32瀏覽量
33944 -
CMOS電路
+關注
關注
0文章
49瀏覽量
11577
發(fā)布評論請先 登錄
相關推薦
簡述基本與非門sr鎖存器的結構及工作原理
與非門的閑置輸入端如何處理
TTL與非門閑置輸入端處理方法
如何使與非門實現(xiàn)反相器的功能
基本rs觸發(fā)器與非門和或非門的區(qū)別
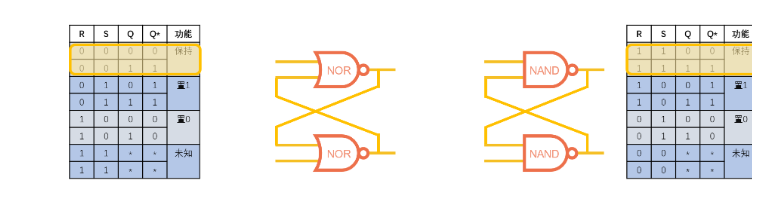
ttl與非門有哪些主要性能參數(shù) TTL與非門的工作原理
cmos或非門電路與ttl或非門電路的邏輯功能
TTL與非門典型電路及其工作原理詳解
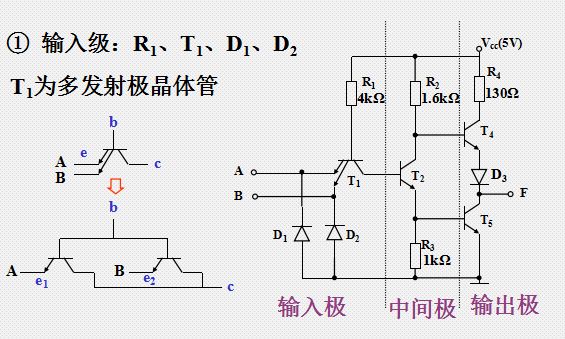




 使用與非門或或非門實現(xiàn)非門的案例解析
使用與非門或或非門實現(xiàn)非門的案例解析











評論