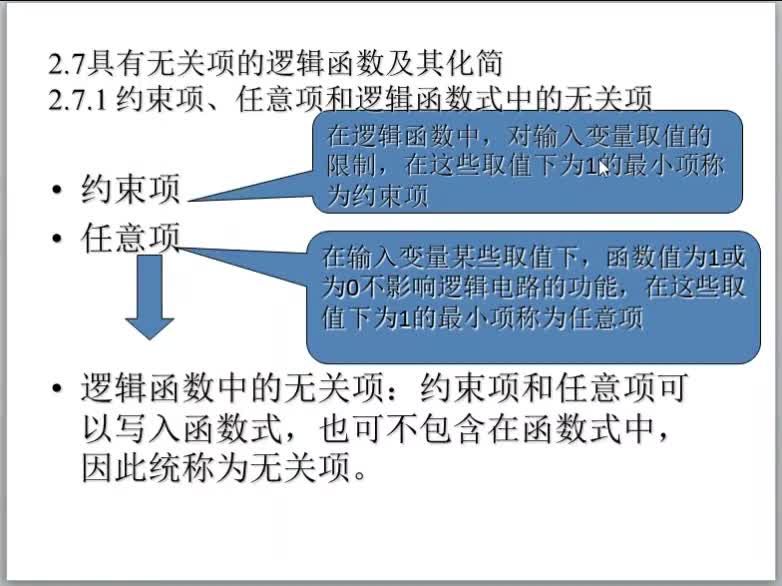
卡諾圖
卡諾圖是邏輯函數的圖形表示。利用卡諾圖可以簡化邏輯函數。
卡諾圖的構成
卡諾圖是最小項按一定規(guī)律排列的方格圖,每一個最小項占有一個小方格。因為最小項的數目與變量數有關,設變量數為n,則最小項的數目為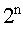 。二個變量的卡諾圖見下圖所示。圖中第一行表示
。二個變量的卡諾圖見下圖所示。圖中第一行表示 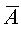 ,第二行表示A;第一列表示
,第二行表示A;第一列表示 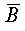 ,第二列表示B。這樣四個小方格就由四個最小項分別對號占有,行和列的符號相交就以最小項的與邏輯形式記入該方格中。
,第二列表示B。這樣四個小方格就由四個最小項分別對號占有,行和列的符號相交就以最小項的與邏輯形式記入該方格中。
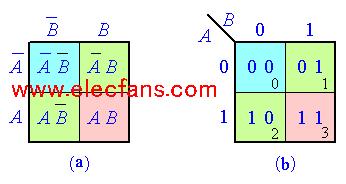
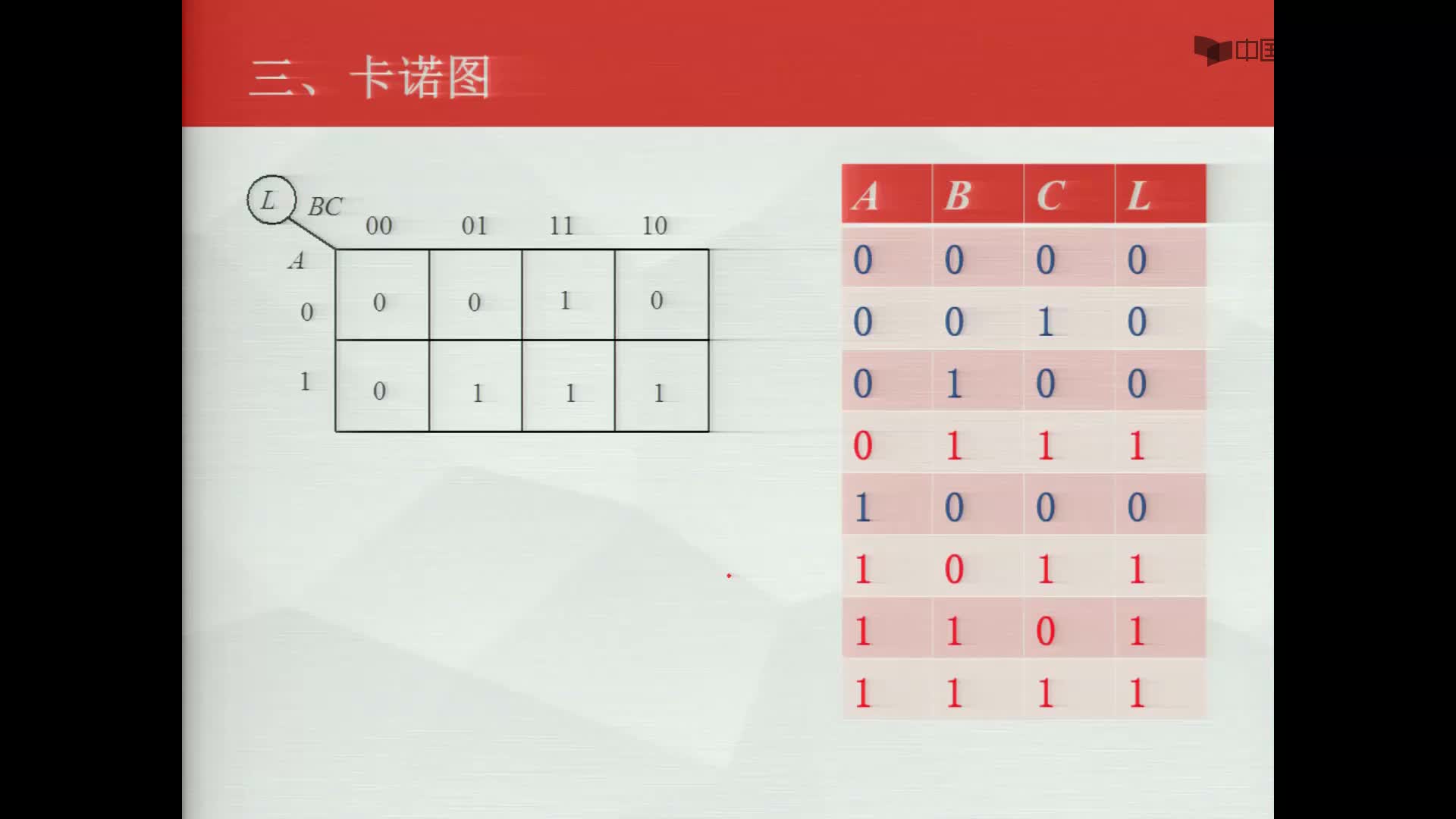
三變量卡諾圖
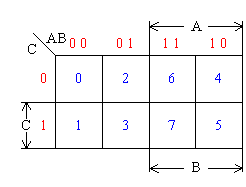
三變量卡諾圖由8個最小項m0—m7組成,每個最小項占一個方格;
AB組合中左數位代表A變量,右數位代表B變量。沿橫向從一個方格進行到下一個方格時,兩個數位只變化一個; 原變量與非變量各占4格。
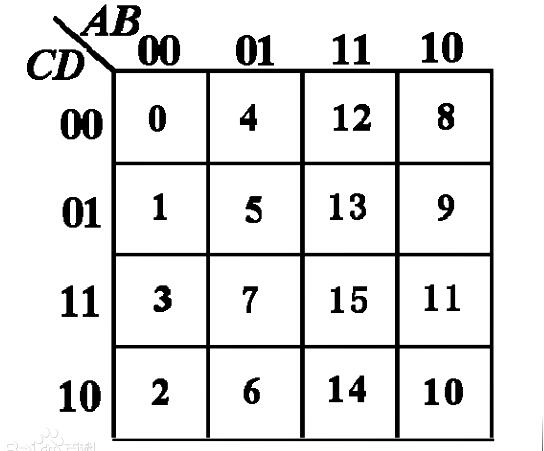
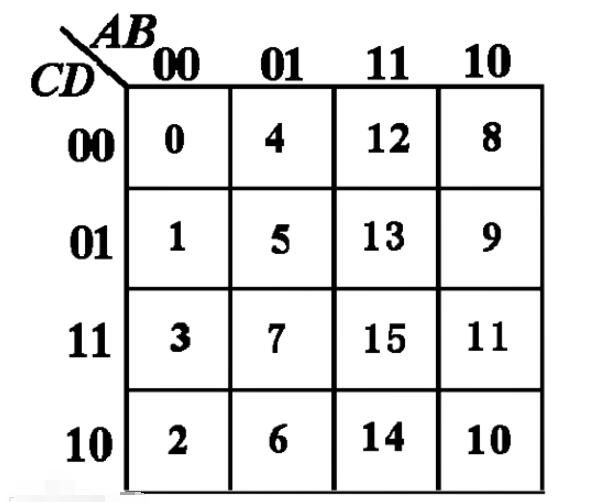
四變量卡諾圖
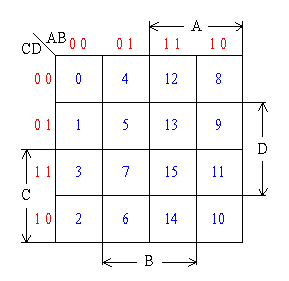
卡諾圖二方格相鄰組合
幾何相鄰的兩個最小項是邏輯相鄰的(兩個最小項中只有一個變量不同);
有些方格幾何上不相鄰,但邏輯上卻是相鄰的;
任何兩個最小項可以合并成最小項,且可減少一個變量。
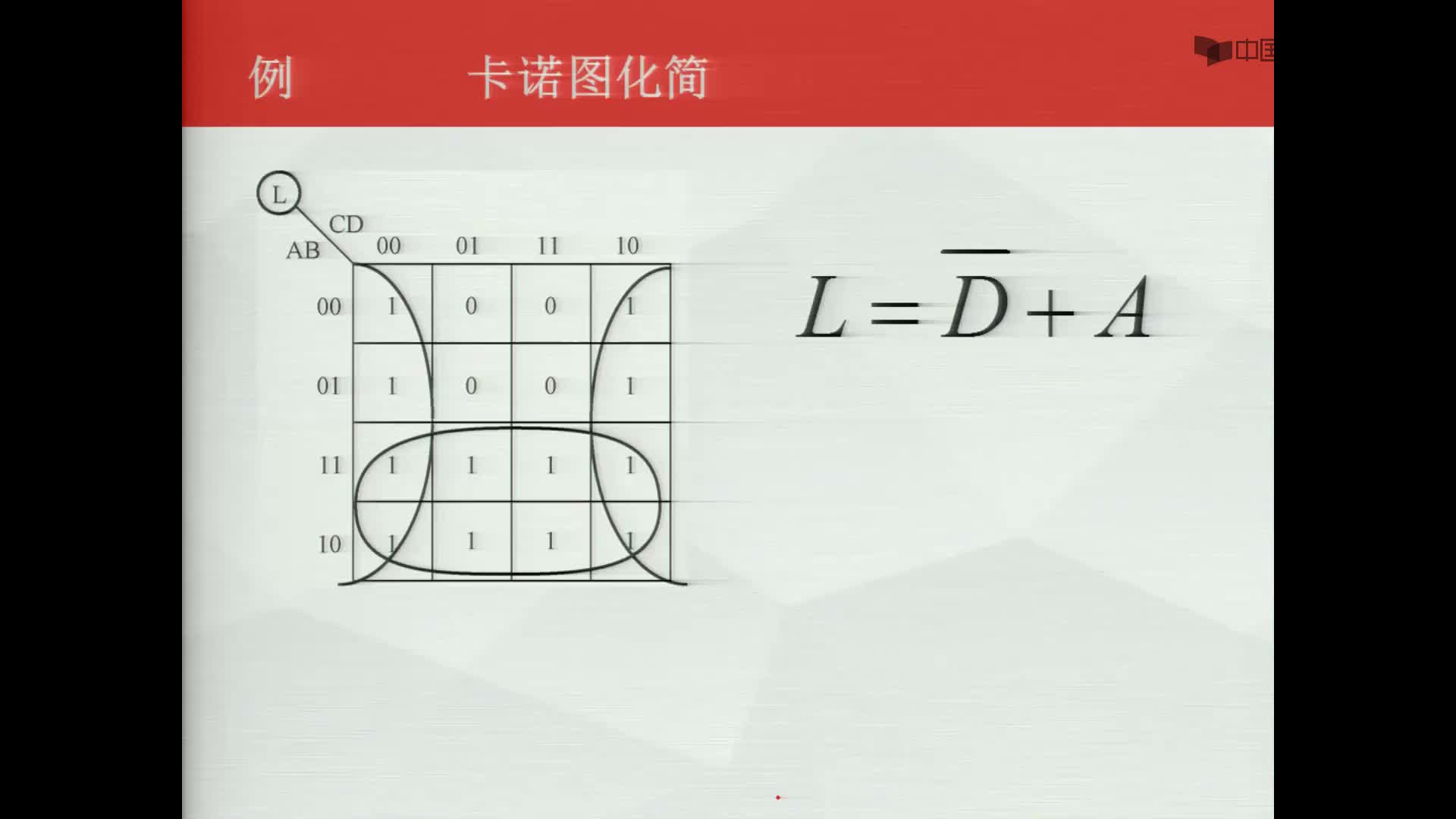
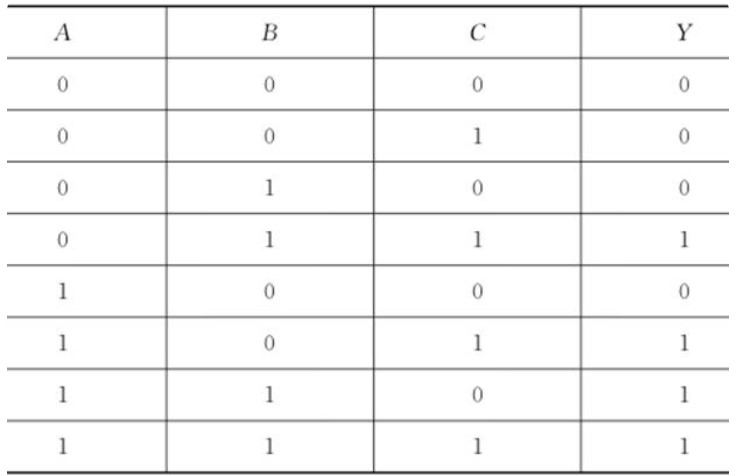
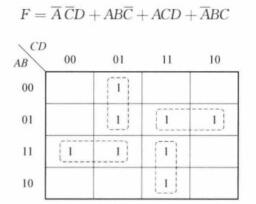
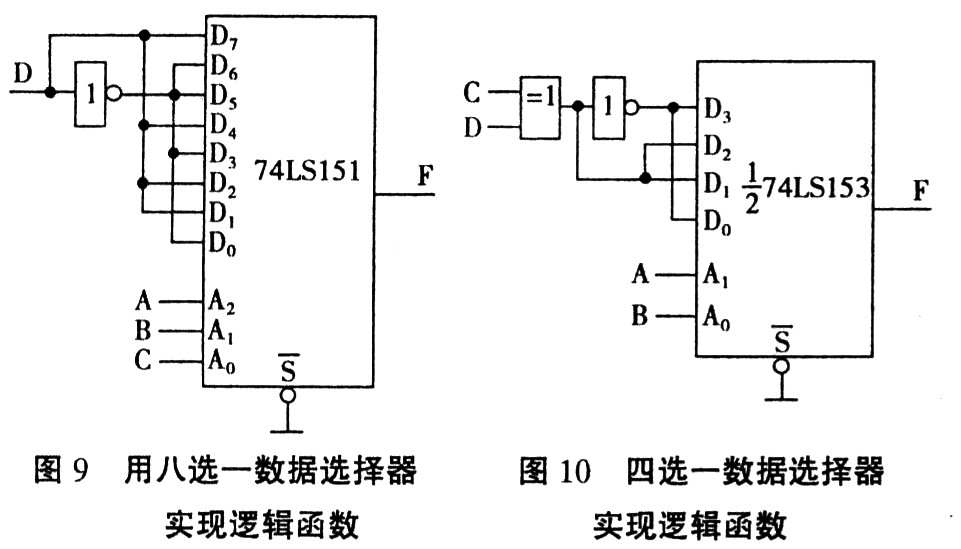
【例3】四方格卡諾圖中,有F(A,B,C,D)=∑m(2,3,8,10,12)
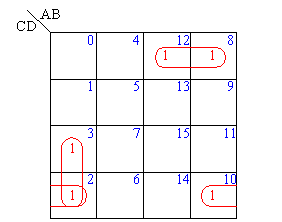
第一種組合方式:
| _ _ | ||
| m8+m12= | A C D | (幾何相鄰) |
| _ _ | ||
| m2+m3= | A B C | (幾何相鄰) |
| _ _ | ||
| m2+m10= | B C D | (幾何不相鄰,邏輯相鄰) |
第二種組合方式:
| _ _ | ||
| m8+m12= | A C D | |
| _ _ | ||
| m2+m3= | A B C | |
| _ _ | ||
| m8+m10= | A B D | (幾何不相鄰,邏輯相鄰) |
| F(A,B,C,D) | =∑m(2,3,8,10,12) |
| _ _ _ _ _ _ | |
| =A C D + A B C + B C D | |
| _ _ _ _ _ _ | |
| =A C D + A B C + A B D |
兩種表達式雖然形式不同,但邏輯上是等價的。另外,m2、m8重復使用是允許的。
卡諾圖四方格相鄰組合
四方格相鄰時,4個最小項可合并成1項,且可消去兩個變量。
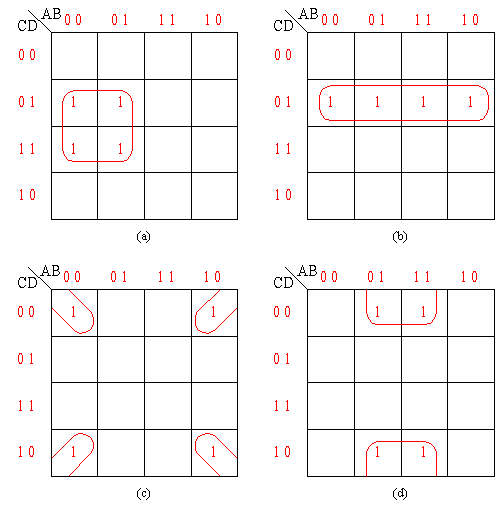
圖(a)中,
| _ | |
| F(A,B,C,D)=∑m(1,3,5,7)= | AD |
圖(b)中,
| _ | |
| F(A,B,C,D)=∑m(1,5,9,13)= | CD |
圖(c)中,
| F(A,B,C,D)=∑m(0,2,8,10)= | ? |
圖(d)中,
| F(A,B,C,D)=∑m(4,6,12,14)= | ? |
卡諾圖八方格相鄰組合
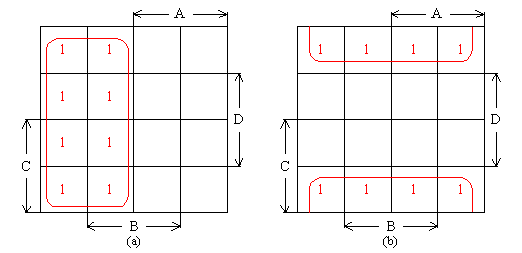
圖(a)中,F(A,B,C,D)=∑m(0,1,2,3,4,5,6,7)=Ã
圖(b)中,F(A,B,C,D)=∑m(0,4,12,8,2,6,14,10)=?
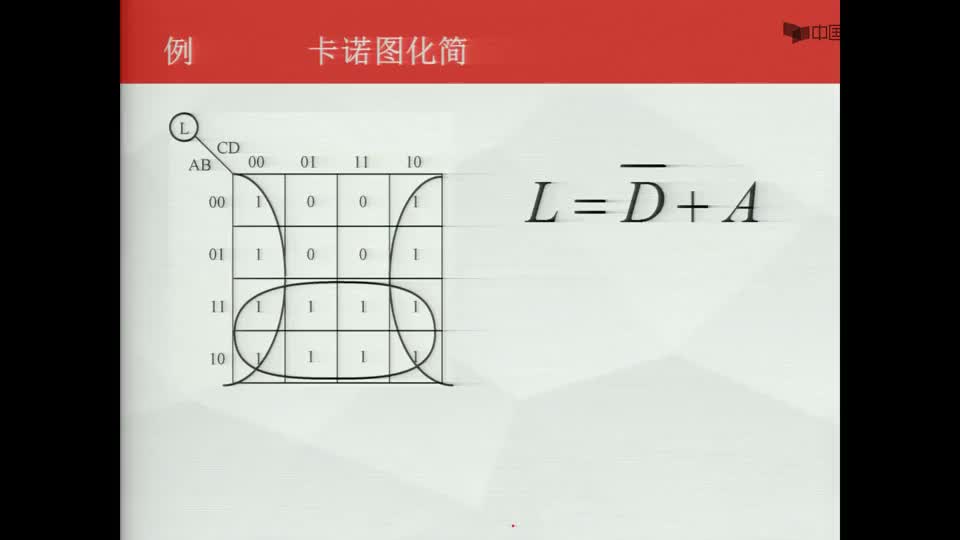
用卡諾圖簡化邏輯函數
簡化規(guī)則
必須使每個方格(最小項)至少被包含一次;
使每個組合包含盡可能多的方格;
所有的方格包含在盡可能少的不同組合中。
簡化步驟
無關項又叫任意項,是一種最小項,其值可以取0或1。利用無關項這一特點,可以使函數簡化。
用卡諾圖化簡邏輯函數的步驟
如果表達式為最小項表達式,則可直接填入卡諾圖
如表達式不是最小項表達式,但是“與—或表達式”,可將其先化成最小項表達式,再填入卡諾圖。也可直接填入。
合并相鄰的最小項,即根據下述原則畫圈
盡量畫大圈,但每個圈內只能含有2n(n=0,1,2,3……)個相鄰項。要特別注意對邊相鄰性和四角相鄰性。
圈的個數盡量少。
卡諾圖中所有取值為1的方格均要被圈過,即不能漏下取值為1的最小項。
在新畫的包圍圈中至少要含有1個末被圈過的1方格,否則該包圍圈是多余的。
寫出化簡后的表達式。每一個圈寫一個最簡與項,規(guī)則是,取值為l的變量用原變量表示,取值為0的變量用反變量表示,將這些變量相與。然后將所有與項進行邏輯加,即得最簡與—或表達式。
在進行化簡時,如果用圖中真值為0的項更方便,可以用他們來處理,方法和真值取1時一樣,只是結果要再做一次求反。
 電子發(fā)燒友App
電子發(fā)燒友App


























































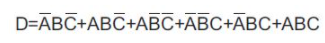

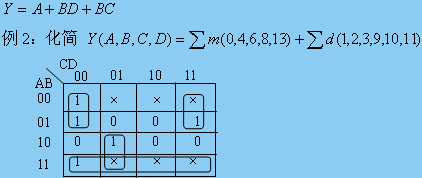










評論