面的夾角,則該點(diǎn)的磁感應(yīng)強(qiáng)度為B=Bm sinα2 交流電路中的電阻、 電容與電感同一電路中電壓和電流的正方向應(yīng)標(biāo)定一致。 
2009-09-24 12:06:25
交流電的三要素是最大值、頻率、初相角。 1)最大值 最大值指正弦交流電在一個(gè)周期內(nèi)出現(xiàn)的最大瞬時(shí)值的絕對值,分別用Ⅰm、Um、Em表示電流、電壓、電動(dòng)勢。 2)頻率 (1)頻率 指交流電在1秒中內(nèi)變化的次數(shù),用f表示,單位為赫茲(Hz),簡稱赫
2023-10-10 10:23:28 205
205 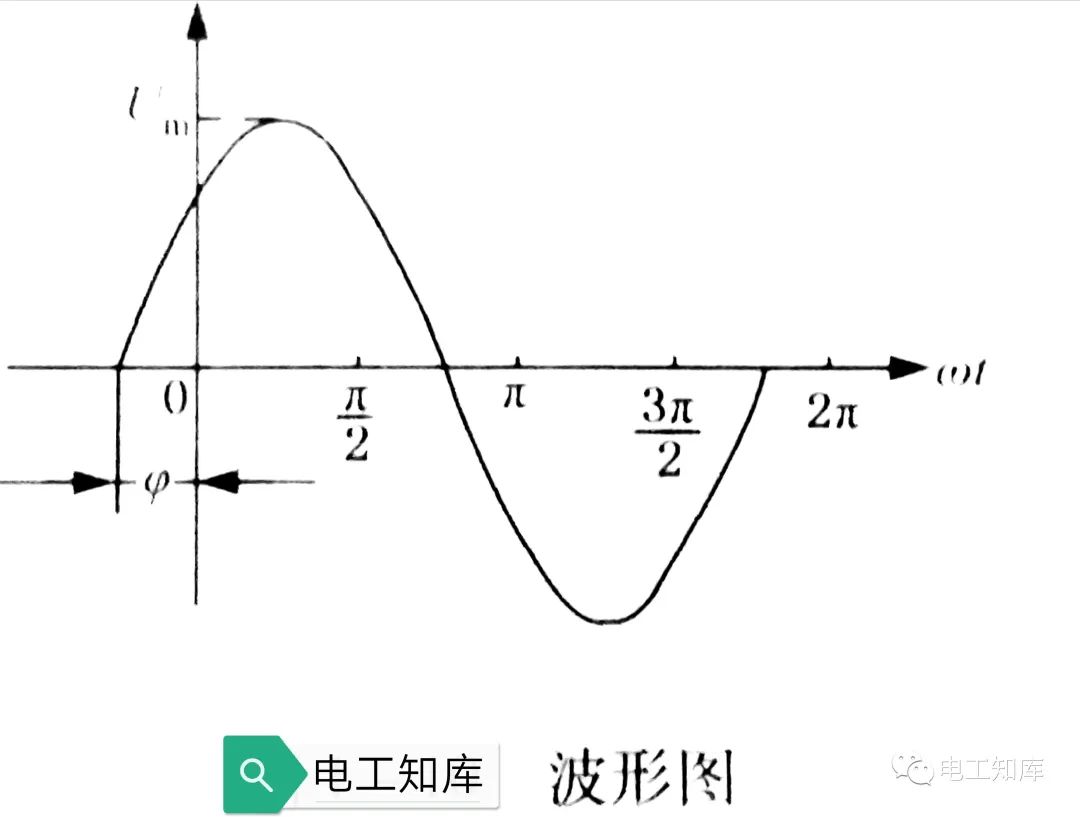
隨時(shí)間按正弦規(guī)律變化的電動(dòng)勢、電壓、電流稱為正弦交流電。 一、周期、頻率、角頻率 1、周期 正弦交流電變化一周所需的時(shí)間叫做周期,用符號T表示,單位是s(秒)。 2、頻率 ls內(nèi)交流電變化的周數(shù)稱為
2023-09-14 11:48:29 493
493 交流電的三要素。 1、最大值 最大值是指正弦交流電在一周期內(nèi)出現(xiàn)的最大瞬時(shí)值的絕對值,用I m 、U m 、E m 分別表示電流、電壓和電動(dòng)勢的最大值。 2、頻率(或角頻率、周期) 一個(gè)按正弦規(guī)律變化的交流電動(dòng)勢從零開始逐漸增至最大值
2023-09-11 16:28:06 511
511 交流電電阻如何測量? 交流電電阻是指電流通過一段電路時(shí),電路對電流的阻礙程度。不同于直流電阻,交流電阻是涉及到振蕩頻率和相位角的量,因此測量起來會更加復(fù)雜。在這篇文章中,我們將會探討如何測量交流電
2023-08-24 14:26:01 468
468 交流電機(jī)簡介 交流電機(jī)是用于實(shí)現(xiàn)機(jī)械能和交流電能相互轉(zhuǎn)換的機(jī)械。由于交流電力系統(tǒng)的巨大發(fā)展,交流電機(jī)已成為最常用的電機(jī)。交流電機(jī)與直流電機(jī)相比,由于沒有換向器(見直流電機(jī)的換向),因此結(jié)構(gòu)簡單,制造
2023-07-05 13:38:10 441
441 本文通過圖文,分享交流電和分類、常見交流電源、交流發(fā)電機(jī)基本工作原理、交流電路等交流電和交流電路方面的基本知識,以期建立對交流電、交流電路的初步概念,為今后進(jìn)一步學(xué)習(xí)交流電路方面各類知識打下基礎(chǔ)。
2023-01-30 16:33:02 3378
3378 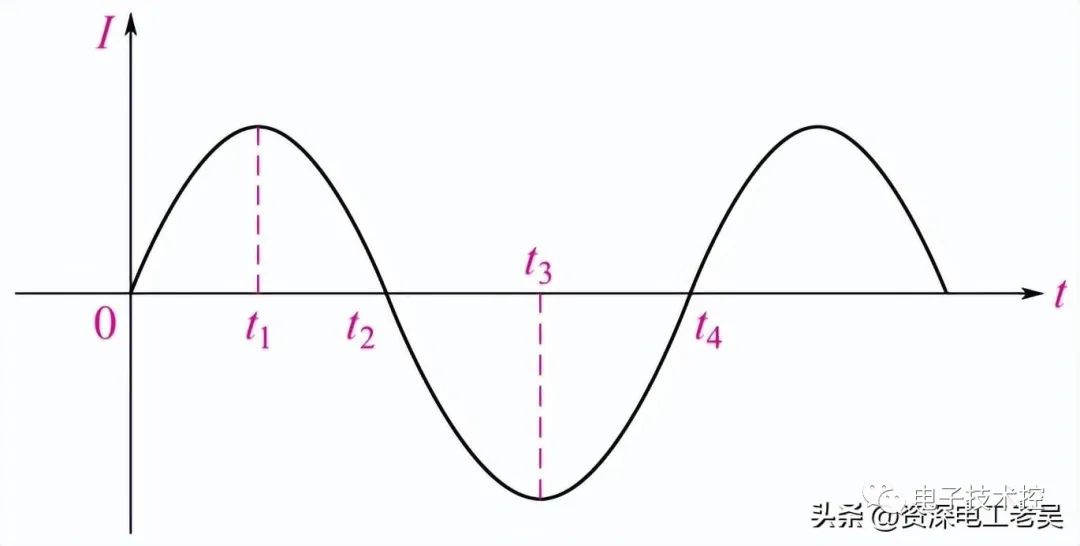
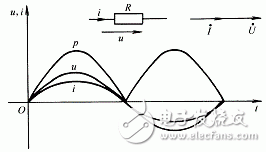
沒有電容和電感,只有電阻的交流電路稱做純電阻交流電路,如圖(a)所示。通過實(shí)驗(yàn)和示波器觀察到電路中電流和電路兩端電壓的波形如圖(b)所示。因而可以得到電流和電壓的矢量圖如圖(c)所示。
2022-08-19 18:20:29 6212
6212 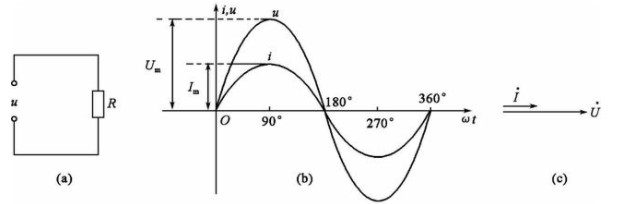
按正弦規(guī)律變化的交流電叫正弦交流電,不按正弦規(guī)律變化的交流電叫非正弦交流電。
2022-08-12 17:59:57 2136
2136 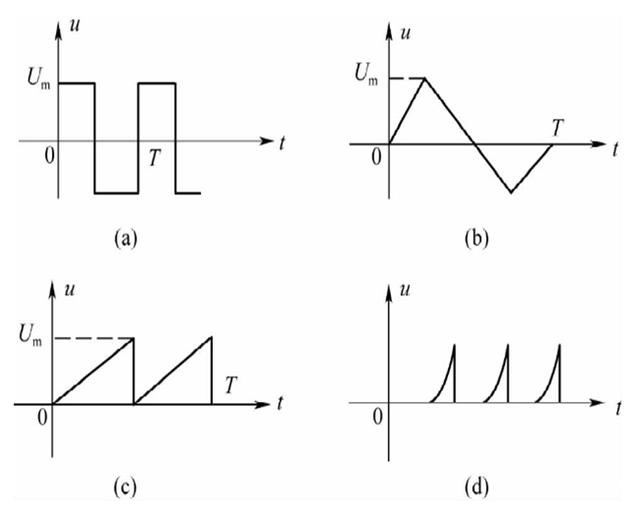
正弦穩(wěn)態(tài)交流電路multisim仿真實(shí)驗(yàn)(電源技術(shù)期刊投稿寫錯(cuò)作者)-該文檔為正弦穩(wěn)態(tài)交流電路multisim仿真實(shí)驗(yàn)講解文檔,是一份不錯(cuò)的參考資料,感興趣的可以下載看看,,,,,,,,,,,,,,,,,
2021-09-24 13:28:25 22
22 交流及正弦交流電(深圳市核達(dá)中遠(yuǎn)通電源技術(shù)有限公司電話多少)-交流及正弦交流電...........................
2021-09-24 13:16:01 9
9 正弦交流電路的原理分析(現(xiàn)代電源技術(shù)基礎(chǔ)課后題答案)-正弦交流電路的原理分析? ? ? ? ? ? ? ??
2021-09-23 16:23:24 18
18 原理1.交流電路正弦交流電的表達(dá)式如下,其曲線如圖6.2.1-1所示。由此可見,正弦交流電的特性表現(xiàn)在正弦交流電的大小、變化快慢及初始值方面。而它們分別由幅值(或有效值)、頻率(或周期)和初相位來確定
2021-09-16 17:47:39 11
11 正弦交流電路練習(xí)試卷資源下載
2021-08-31 09:17:21 4
4 交流電橋是測量各種交流阻抗的基本儀器,如電容的電容量,電感的電感量等。此外還可利用交流電橋平衡條件與頻率的相關(guān)性來測量與電容、電感有關(guān)的其他物理量,如互感、磁性材料的磁導(dǎo)率、電容的介質(zhì)損耗、介電常數(shù)和電源頻率等,其測量準(zhǔn)確度和靈敏度都很高,在電磁測量中應(yīng)用極為廣泛。
2021-01-15 15:28:32 12886
12886 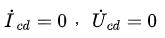
頻率的單位現(xiàn)統(tǒng)一采用赫茲,簡稱赫,以符號Hz表示。在工農(nóng)業(yè)生產(chǎn)上使用的交流電一般是50Hz;話音頻率約為100—5000Hz;在無線電技術(shù)及電子技術(shù)中所用的頻率從數(shù)赫到幾萬兆赫(MHz)。較高的頻率單位常用千赫(KHz)或兆赫(MHz)。
2021-01-02 16:55:00 49022
49022 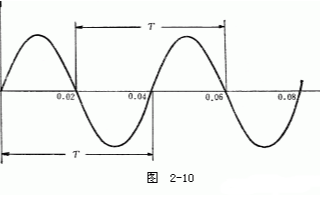
正弦交流電變化過程中的最大值,稱為正弦交流電的極大值(或叫振幅值)。由于發(fā)電機(jī)中磁極的對稱性,所以交流電在正半周和負(fù)半周應(yīng)該對稱。它們的極大值也是一樣的。例如,對于式(2-7)由于sinωt最大等于1,所以sinωt前面的值,即為電勢的最大值。
2021-01-02 16:52:00 11115
11115 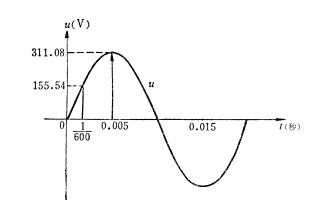
本文檔的主要內(nèi)容詳細(xì)介紹的是單相正弦交流電路的學(xué)習(xí)課件免費(fèi)下載包括了:一,測量基礎(chǔ)知識二,正弦交流電路的基本物理量三,純電阻、純電感、純電容電路,四串聯(lián)電路五,交流電路的功率
2020-10-14 16:37:00 12
12 交流電是指大小和方向都發(fā)生周期性變化電壓。通常為正弦交流電,但實(shí)際中也存在方波交流電、三角形波交流電等。
2020-03-13 11:31:58 94225
94225 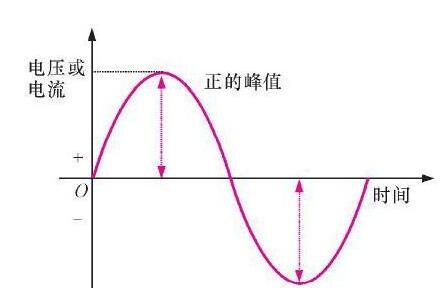
Imax為交流電的峰值,ω為交流電在磁場轉(zhuǎn)動(dòng)的角速度,ωt為交流電在磁場中轉(zhuǎn)動(dòng)的弧度,如果t為交流電變化的一個(gè)周期的話,那么ωt就等于2π(假設(shè)此交流電的初相位為0),則此時(shí)的交流電的瞬時(shí)電流值就為0。
2020-03-11 10:30:55 3105
3105 本文檔的主要內(nèi)容詳細(xì)介紹的是正弦交流電路的經(jīng)典復(fù)習(xí)題詳細(xì)解答。
2020-02-27 08:00:00 6
6 正弦交流電的三種表示法一般有四種表示方法:解析法、曲線法、旋轉(zhuǎn)矢量法和符號法。
2019-12-16 14:33:15 24130
24130 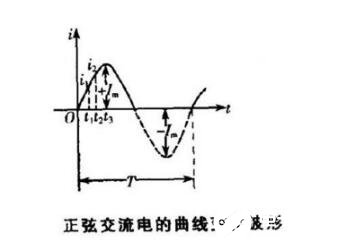
電流是正弦交流電流,則其周圍的磁場也是正弦變化的磁場。由于電磁感應(yīng)原理的作用,當(dāng)交流電壓通過線圈時(shí),線圈周圍會產(chǎn)生磁場。這是大家熟知的知識,下面以正弦電流為例,分析一下周圍磁場的變化。
2019-10-13 04:58:00 10258
10258 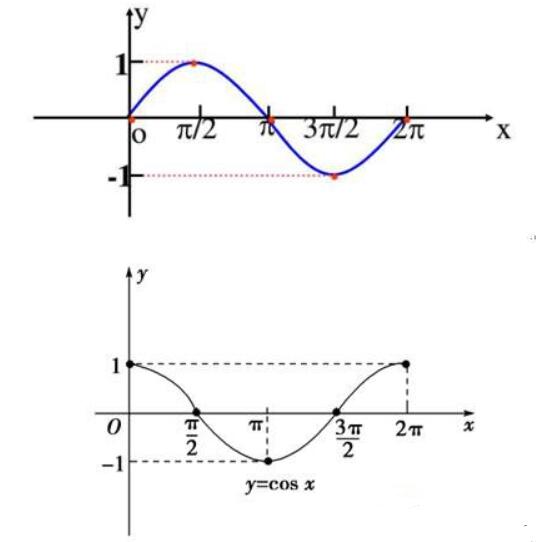
以歐姆為單位測量的阻抗是對包含電阻和電抗的交流電路周圍的電流的有效阻抗,在我們知道如何表示電壓或電流作為相量,當(dāng)連接到單相交流電源時(shí),我們可以將這種關(guān)系應(yīng)用于基本的無源電路元件,例如交流電阻。
2019-06-27 15:13:34 5377
5377 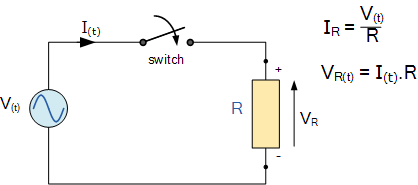
交流電大小和方向都隨時(shí)間按一定規(guī)律作周期性變化的電壓、電流和電勢,稱為交流電。
按正弦曲線規(guī)律變化的交流電,稱為正弦交流電。
2018-10-31 08:00:00 13
13 本文主要介紹了正弦交流電路中的計(jì)算公式及計(jì)算案例分析。視在功率S定義:電路中總電壓與總電流有效值的乘積。又稱為容量,表征的是電源能夠提供的最大有功功率,但電源實(shí)際輸出的有功功率的大小取決于負(fù)載。
2018-08-30 17:08:20 60294
60294 本文主要詳細(xì)闡述了六種可以產(chǎn)生正弦交流電的方式。線框在勻強(qiáng)磁場中勻速轉(zhuǎn)動(dòng)產(chǎn)生正弦交流電,這是產(chǎn)生正弦交流電的最基本方式,也是感應(yīng)發(fā)電機(jī)的原理。線框的轉(zhuǎn)動(dòng)軸一般跟磁場方向垂直,線框平面跟磁場方向垂直的位置叫中性面。在中性面處磁通量最大,而感應(yīng)電動(dòng)勢最小為零。
2018-08-28 17:35:36 41358
41358 本文主要詳細(xì)闡述了正弦交流電的有效值。正弦交流電是指大小和方向都隨時(shí)間按正弦規(guī)律作周期性變化的電流(或電壓),也叫簡諧交流電。我們?nèi)粘S玫碾姸际?b style="color: red">正弦交流電,它是各種形式的交流電中最為基本和重要的。
2018-08-28 17:28:25 60978
60978 本文首先介紹了正弦交流電的產(chǎn)生,其次介紹了單相交流電的產(chǎn)生,最后介紹了兩相交流電的產(chǎn)生。正弦交流電是由交流發(fā)電機(jī)產(chǎn)生的,而發(fā)電機(jī)則是利用電磁感應(yīng)的原理,將機(jī)械能轉(zhuǎn)變?yōu)殡娔艿难b置。常見的交流異步電動(dòng)機(jī)
2018-08-28 17:15:26 14551
14551 本文主要詳細(xì)闡述了正弦交流電的三種表示方法,分別為解析法、正弦曲線法以及旋轉(zhuǎn)相量法。
2018-08-25 10:47:07 11710
11710 本文主要詳細(xì)的闡述了正弦交流電應(yīng)用以及發(fā)展的意義。
2018-08-25 10:01:44 4759
4759 本文首先介紹了什么是正弦交流電,其次介紹了正弦交流電三要素,最后闡述了正弦交流電的特點(diǎn)。
2018-08-25 09:54:34 105762
105762 提出了一種快速數(shù)控 SPWM 的實(shí)現(xiàn)方法 , 建立了正弦交流電流源穩(wěn)流模糊 PID 控制算法模型 , 應(yīng)用 MSP430 單片機(jī)研制了樣機(jī) , 能提供 0~10A 步進(jìn)為 10mA 、頻率為 0
2018-04-28 09:10:40 24
24 交流電的頻率是指它單位時(shí)間內(nèi)周期性變化的次數(shù),單位是赫茲(Hz),與周期成倒數(shù)關(guān)系。日常生活中的交流電的頻率一般為50Hz,而無線電技術(shù)中涉及的交流電頻率一般較大,達(dá)到千赫茲(KHz)甚至兆赫茲(MHz)的度量。
2017-12-25 15:34:05 12783
12783 
交流電是指大小和方向都發(fā)生周期性變化的電流,因?yàn)?b style="color: red">周期電流在一個(gè)周期內(nèi)的運(yùn)行平均值為零,稱為交變電流或簡稱交流電。不同直流電,其方向都是一樣。通常波形為正弦曲線。交流電可以有效傳輸電力。但實(shí)際上還有應(yīng)用其他的波形,例如三角形波、正方形波。生活中使用的市電就是具有正弦波形的交流電。
2017-12-23 11:04:55 200729
200729 
交流電,簡稱為AC。交流電也稱“交變電流”,簡稱“交流”。電流方向隨時(shí)間作周期性變化的為交流電。它的最基本的形式是正弦電流。當(dāng)法拉第發(fā)現(xiàn)了電磁感應(yīng)后,產(chǎn)生交流電流的方法則被法拉第同時(shí)發(fā)現(xiàn),法拉第因此被譽(yù)為“交流電之父”。
2017-11-05 15:14:24 158359
158359 什么是正弦交流電?什么是正弦交流電的三要素? 所謂正弦交流電是指大小和方向都按正弦規(guī)律作周期性變化的電動(dòng)勢(電壓或電流)。正弦交流電的三要素是:最大值、角頻率和初相角。
2017-09-11 17:07:27 15
15 大小和方向隨時(shí)間作有規(guī)律變化的電壓和電流稱為交流電,又稱交變電流。正弦交流電是隨時(shí)間按照正弦函數(shù)規(guī)律變化的電壓和電流。由于交流電的大小和方向都是隨時(shí)間不斷變化的,也就是說,每一瞬間電壓(電動(dòng)勢)和電流的數(shù)值都不相同。
2017-07-20 11:30:39 25657
25657 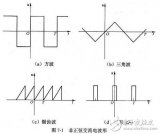
正 弦量:大小和方向隨時(shí)間按正弦規(guī)律變化的電壓、電流統(tǒng)稱為正弦量。正弦信號的和、差、微積分等運(yùn)算結(jié)果仍是同頻率的正弦信號。當(dāng)正弦信號作為電路的信號源時(shí),電路中產(chǎn)生的響應(yīng)仍是同頻率的正弦信號。
2017-05-05 09:24:16 26906
26906 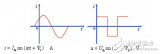
大小和方向隨時(shí)間作有規(guī)律變化的電壓和電流稱為交流電,又稱交變電流。正弦交流電是隨時(shí)間按照正弦函數(shù)規(guī)律變化的電壓和電流。由于交流電的大小和方向都是隨時(shí)間不斷變化的,也就是說,每一瞬間電壓(電動(dòng)勢)和電流的數(shù)值都不相同,所以在分析和計(jì)算交流電路時(shí),必須標(biāo)明它的正方向。
2017-05-05 09:04:57 19032
19032 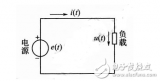
家庭、商用、工業(yè)上被廣泛應(yīng)用的大多都是交流電。之所以叫做交流電是因?yàn)槠浯笮『头较蚨际请S時(shí)間不斷交替變換的電流,簡稱交流。在交變電動(dòng)勢作用下,電路中的電流、電壓都是交變的,這樣的電路叫做交流電路。
2017-05-03 09:09:21 37087
37087 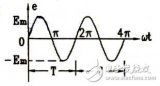
正弦交流電是隨時(shí)間按照正弦函數(shù)規(guī)律變化的電壓和電流。由于交流電的大小和方向都是隨時(shí)間不斷變化的,也就是說,每一瞬間電壓(電動(dòng)勢)和電流的數(shù)值都不相同,所以在分析和計(jì)算交流電路時(shí),必須標(biāo)明它的正方
2017-05-02 11:11:16 18556
18556 一、直流電 直流電的大小和方向都不隨時(shí)間而變化的。 二、交流電 交流電的大小和方向是隨時(shí)間不斷變化的; 日常供電部門供給我們的電是正弦交流電; 正弦交流電的大小和方向是隨時(shí)間按正弦規(guī)律作周期變化
2017-01-17 11:03:26 5961
5961 的發(fā)電機(jī),成本也低,容易維護(hù)。本章主要介紹正弦交流電路的基本概念;電阻、電感、電容元件在交流電路中的特性;阻抗串聯(lián)、并聯(lián)的特點(diǎn);交流電路的有功功率、無功率功率和視在功率;交流電路功率因數(shù)及提高功率因數(shù)的意義及方
2016-06-22 15:56:11 9
9 《電路基礎(chǔ)(第3版)》講述了電路分析的基本理論,共分為三篇:直流電路、交流電路以及高級電路分析。第二篇交流電路主要講述相量、正弦穩(wěn)態(tài)分析、交流功率分析、三相電路、磁耦合電路以及頻率響應(yīng)等。
2016-04-25 14:22:40 12
12 電感、電容在正弦交流電路中的特性下載下倆對你的對電子的認(rèn)識會有很大的幫助與提供
2015-12-14 15:53:13 5
5 本文基于探索正弦交流電路中電感L、電容C元件特性的目的,運(yùn)用Multisim10軟件對L、C元件的特性進(jìn)行了仿真實(shí)驗(yàn)分析,給出了Multisim仿真實(shí)驗(yàn)方案,仿真了電感、電容元件的交流電壓和電
2013-07-25 12:08:44 148
148 一個(gè)最簡輸入正弦交流電信號變?yōu)殇忼X波電信號的電路。鋸齒波電信號的頻率為正弦交流電信號頻率的2倍。且與之嚴(yán)格同步,非常適合作可控硅交流調(diào)壓的觸發(fā)脈沖信號以及直流電機(jī)調(diào)
2012-04-01 10:54:16 5482
5482 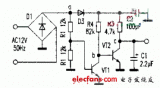
概述
§3.2 非正弦周期交流信號的分解
§3.3 非正弦周期交流電路的分析和計(jì)算
§3.4 非正弦周期交流信號的平均值、有效值、平均功率的計(jì)算
2010-08-16 17:06:20 67
67 交流電阻電橋
即使純電阻交流
2009-11-14 08:26:03 2161
2161 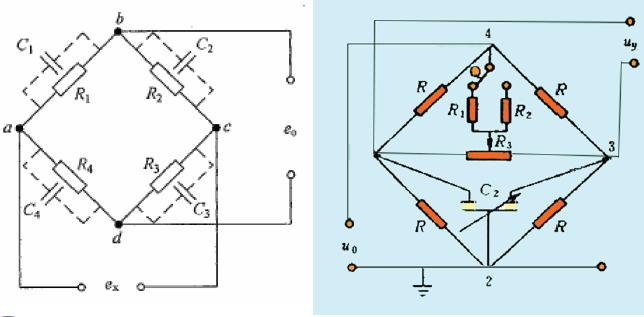
電阻元件在正弦交流電路中的作用1 電阻中的電流與電壓同相2 如何計(jì)算流經(jīng)電阻的電流3 如何計(jì)算電阻消耗的功率
2009-09-22 09:46:20 1782
1782 正弦交流電的有效值
如圖所示,正弦交流電流的大小在各個(gè)瞬間是不相同的,在每一瞬間時(shí)電流的值稱為瞬時(shí)值。在每半個(gè)周期內(nèi),
2009-09-22 09:43:27 4620
4620 
RC在交流電路中的作用
本章首先介紹正弦交流電,然后講述RC元件及RC串聯(lián)電路在正弦電路中的作用,最后講解RC串聯(lián)電路在不同頻率正弦信號作用下
2009-09-22 09:30:42 30
30 復(fù)雜正弦交流電路的計(jì)算
在一個(gè)電網(wǎng)絡(luò)中,如果所有的激勵(lì)源(電壓源與電流源)都是同一頻率的正弦函數(shù),電路所有元件均為線性元
2009-07-27 09:46:41 1665
1665 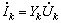
正弦交流電路的功率計(jì)算
如果一端口網(wǎng)絡(luò)的端口電壓
2009-07-27 09:24:51 16238
16238 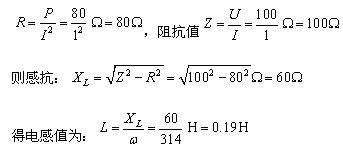
正弦交流電路的阻抗、導(dǎo)納及等效轉(zhuǎn)換
前面幾節(jié)已導(dǎo)出電阻、電感和電容元件上電壓與電流的相量關(guān)系,引入了電抗和容抗的概念。當(dāng)
2009-07-27 08:44:35 8902
8902 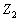
正弦交流電路中的電容元件
線性非時(shí)變電容元件C兩端加上交流電壓時(shí),電
2009-07-27 08:42:02 5715
5715 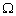
正弦交流電路中的電感元件
線性非時(shí)變電感元件是電路中一種重要和基本的元件,在實(shí)際電路中經(jīng)常遇到由導(dǎo)線繞制而成的電感線圈。
2009-07-27 08:39:35 6784
6784 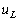
正弦交流電路中的電阻元件
電阻元件兩端的電壓與通過它的電流之間關(guān)系受歐姆定律約束。當(dāng)正弦電流流過
2009-07-27 08:37:49 3603
3603 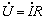
正弦交流電量的相量表示
正弦量除了用波形和瞬時(shí)表達(dá)式來表示以外,利用歐拉公式還可以表示成復(fù)指數(shù)的形式。一個(gè)正弦交流電流
2009-07-27 08:30:52 9220
9220 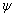
正弦交流電量的基本概念
在直流電路中,電壓和電流的大小、方向都不隨時(shí)間變化。如果電路中電壓和電流隨時(shí)間作周期性變化,且在
2009-07-27 08:24:02 1211
1211 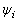
對稱三相正弦交流電路
三相制供電是電力系統(tǒng)普遍采用的供電方式,所謂三相制就是由三個(gè)頻率相同、相位不同的電源作
2009-07-27 08:20:02 10565
10565 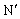
1、阻抗與導(dǎo)納的概念及意義 2、正弦交流電路的相量法 3、功率因素的提高 4、最大功率傳輸 1、利用相量圖進(jìn)行復(fù)雜
2009-07-08 09:12:39 48
48
電容/交流電壓轉(zhuǎn)換電路
2009-02-22 11:29:06 3313
3313 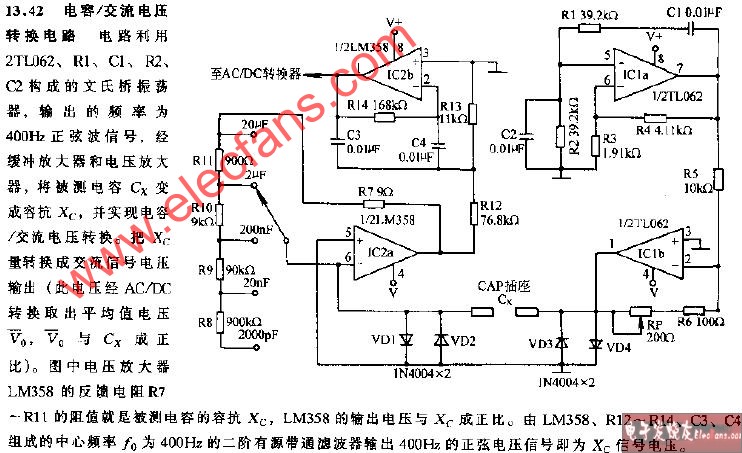
正弦交流電路.PPT4.1 正弦電壓與電流4.2 正弦量的相量表示法4.3 電阻元件、電感元件與電容元件4.4 電阻元件交流電路4.5
2008-12-04 14:02:07 79
79 第5章 三相正弦交流電路5 .1 三相電源目的與要求重點(diǎn)與難點(diǎn)5.1.1 三相對稱正弦交流電壓(一)5.1.1 三相對稱正弦交流電壓(二)5.1.1 三相對
2008-11-02 23:49:11 99
99 實(shí)驗(yàn) 單項(xiàng)正弦交流電路的分析一. 實(shí)驗(yàn)?zāi)康?
1. 研究正弦穩(wěn)態(tài)交流電路中電壓、電流相量之間的關(guān)系。
2.
2008-11-02 22:27:38 6850
6850 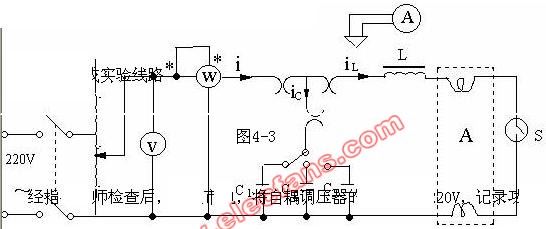
交流電路中基本參數(shù)電阻、電感和電容的測量
一、實(shí)驗(yàn)?zāi)康摹 ?、了解交流電路中R、L、C元件的頻率與阻抗之間的關(guān)系,測定R-f、XL-f、XC-f特性曲
2008-10-17 23:06:40 10973
10973 什么是正弦交流電的瞬時(shí)值,最大值,有效值和平均值?瞬時(shí)值:正弦交流電每時(shí)每刻都是變化的,在某一時(shí)刻的數(shù)
2008-10-04 15:50:13 14059
14059 
什么是正弦交流電的相位,初相角和相位差?
2008-10-04 15:46:53 16399
16399 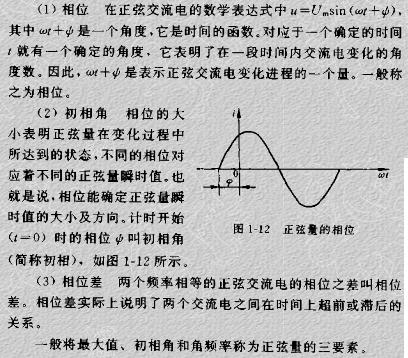
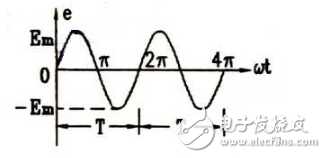
什么是正弦交流電的周期,頻率和角頻率?
2008-10-04 15:45:24 18719
18719 
什么是正弦交流電?什么是市電?大小和方向均隨時(shí)間作有規(guī)律變化的電壓和電流稱為交流電。所謂正弦交流電是指隨著時(shí)間按正比函數(shù)規(guī)律周期性變化的
2008-10-04 15:43:02 4769
4769 
正弦交流電路中R、L、C元件性能
一、實(shí)驗(yàn)?zāi)康?⒈ 研究RLC元件在正弦交流電路中的基本特性。?⒉ 研究RLC并聯(lián)電路中總電流與分
2008-09-24 20:42:43 11391
11391 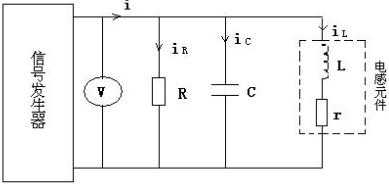
交流電路頻率特性的測定
一.實(shí)驗(yàn)?zāi)康?1.研究電阻,感抗、容抗與頻率的關(guān)系,測定它們隨頻率變化的特性曲
2008-09-22 16:02:13 6951
6951 正弦穩(wěn)態(tài)交流電路相量的研究
一.實(shí)驗(yàn)?zāi)康模保芯?b style="color: red">正弦穩(wěn)態(tài)交流電路中電壓、電流相量之間的關(guān)系?2
2008-09-22 15:51:10 21944
21944 在日常生活中所用的就是單相正弦交流電,簡稱交流電。本章主要介紹交流電的相量表示法及電阻、電感、電容元件在交流電路中的電流、電壓和功率的分析法。交流電的三要
2008-08-16 13:44:47 103
103
正在加载...
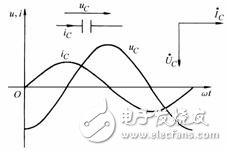
![]() 時(shí),電容中就將有電流
時(shí),電容中就將有電流![]() 流過。若取電容元件支路
流過。若取電容元件支路![]() 的參考方向與電壓
的參考方向與電壓![]() 的參考方向一致,如圖1所示,則有:
的參考方向一致,如圖1所示,則有:![]() 時(shí),電容電流為
時(shí),電容電流為![]() 與電流
與電流![]() 為同頻率的正弦量,電流
為同頻率的正弦量,電流![]() 在相位上超前電壓
在相位上超前電壓![]() 。從波形圖上可看出,當(dāng)電容電壓過零值時(shí),電壓的變化率最大,此時(shí)流過電容的電流幅值達(dá)到最大振幅值。而當(dāng)電容電壓達(dá)到最大幅值時(shí),其電壓變化率為零,此時(shí)通過電容的電流值也為零。類似于電感元件的情況,電容元件的電流與電壓在某些時(shí)刻方向一致,而在另一些時(shí)刻方向則相反。
。從波形圖上可看出,當(dāng)電容電壓過零值時(shí),電壓的變化率最大,此時(shí)流過電容的電流幅值達(dá)到最大振幅值。而當(dāng)電容電壓達(dá)到最大幅值時(shí),其電壓變化率為零,此時(shí)通過電容的電流值也為零。類似于電感元件的情況,電容元件的電流與電壓在某些時(shí)刻方向一致,而在另一些時(shí)刻方向則相反。![]() 與電壓有效值
與電壓有效值![]() 之間的關(guān)系為
之間的關(guān)系為![]() ,稱為電容的電抗,簡稱為容抗。當(dāng)電容C的單位為法拉(F),
,稱為電容的電抗,簡稱為容抗。當(dāng)電容C的單位為法拉(F),![]() 的單位為
的單位為![]() 時(shí),容抗的單位為
時(shí),容抗的單位為![]() ,與電阻的量綱相同。
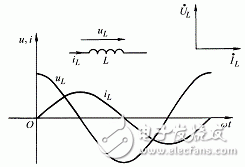
,與電阻的量綱相同。![]() ,代入上式可得電感元件兩端的電壓為
,代入上式可得電感元件兩端的電壓為![]() 是與
是與![]() 同頻率的正弦量,電壓
同頻率的正弦量,電壓![]() 的相位超前電流
的相位超前電流![]() 周期,即
周期,即![]() 或
或![]() 。
。![]() 與電感端電壓的有效值之間有關(guān)系式
與電感端電壓的有效值之間有關(guān)系式![]() 叫做電感線圈的自感電抗,簡稱感抗,它和電阻具有相同的量綱。當(dāng)電感L的單位取H,角頻率
叫做電感線圈的自感電抗,簡稱感抗,它和電阻具有相同的量綱。當(dāng)電感L的單位取H,角頻率![]() 的單位取
的單位取![]() 時(shí),感抗的單位為
時(shí),感抗的單位為![]() 。感抗一般用字母
。感抗一般用字母![]() 表示,即
表示,即![]() ,設(shè)流過電流
,設(shè)流過電流![]() ,頻率
,頻率![]() ,問線圈電壓
,問線圈電壓![]() 為多少?若電流頻率
為多少?若電流頻率![]() ,重求線圈端電壓
,重求線圈端電壓![]() 。
。![]() ,當(dāng)頻率
,當(dāng)頻率![]() 時(shí),感抗
時(shí),感抗 電子發(fā)燒友App
電子發(fā)燒友App





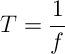























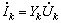
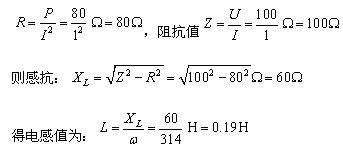
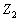
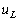
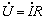
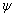
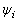

















評論