本節主要是對通用無源電路網絡的原理圖構建和電路仿真。主要介紹了電路方程的改進節點法和原理圖構建中所使用的圖論相關分析方法。最后結合實際濾波器電路,使用Matlab實現了一個通用無源網絡仿真引擎,附Github鏈接。
通用無源網絡仿真(AC和瞬態)
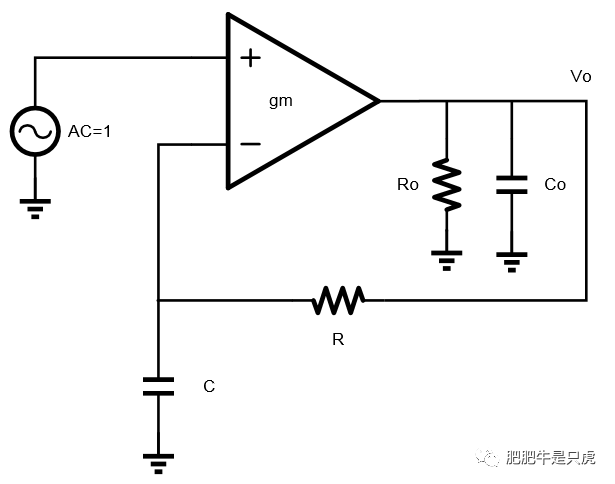
模擬無源濾波器設計(三)-通用梯形電路網絡分析和仿真中所介紹的電路網絡分析只是針對梯形無源網絡,由于使用了網孔分析的方法,所以還存在諸多缺陷:
對于為0的電容,其阻抗為無窮大,網孔方程將無法列解
由于濾波器設計非常關注其瞬態響應,之前的方程將不能滿足瞬態響應的數值求解
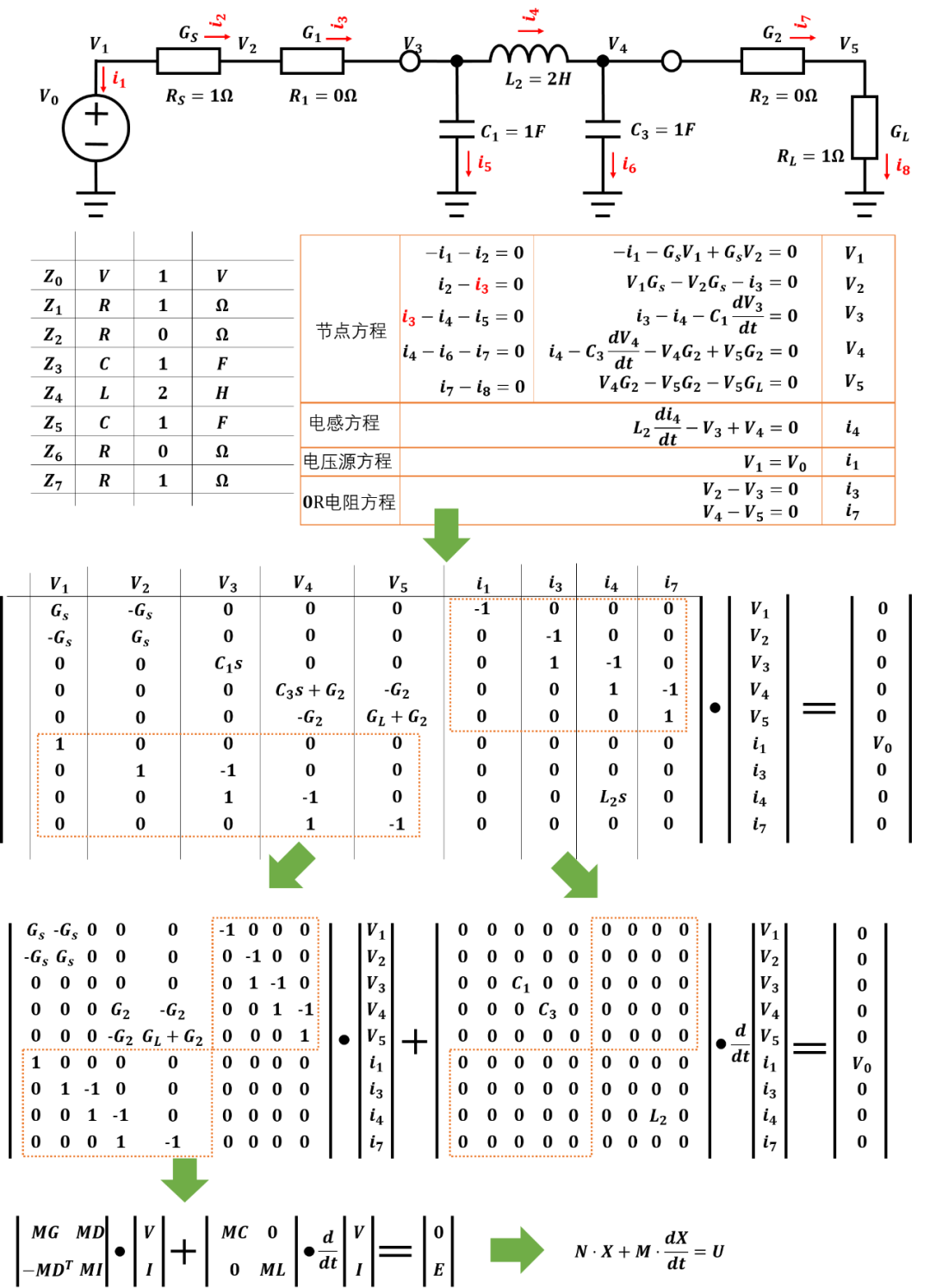
基于以上兩點,電路方程將使用改進的節點方程形式(The modified node equation):?這種方程形式將電路方程分解為兩部分,一部分是微分電路矩陣??,一部分是常數電路矩陣??,這種形式方程可以非常容易進行數值分析和處理。 式中M矩陣中包含電路中所有的微分電路器件,如電感的電壓就是其電流的微分形式??,電容的電流是其電壓的微分形式??.而N中包含電路的電阻和電導器件,如電阻??。 方程構建過程如下圖所示:
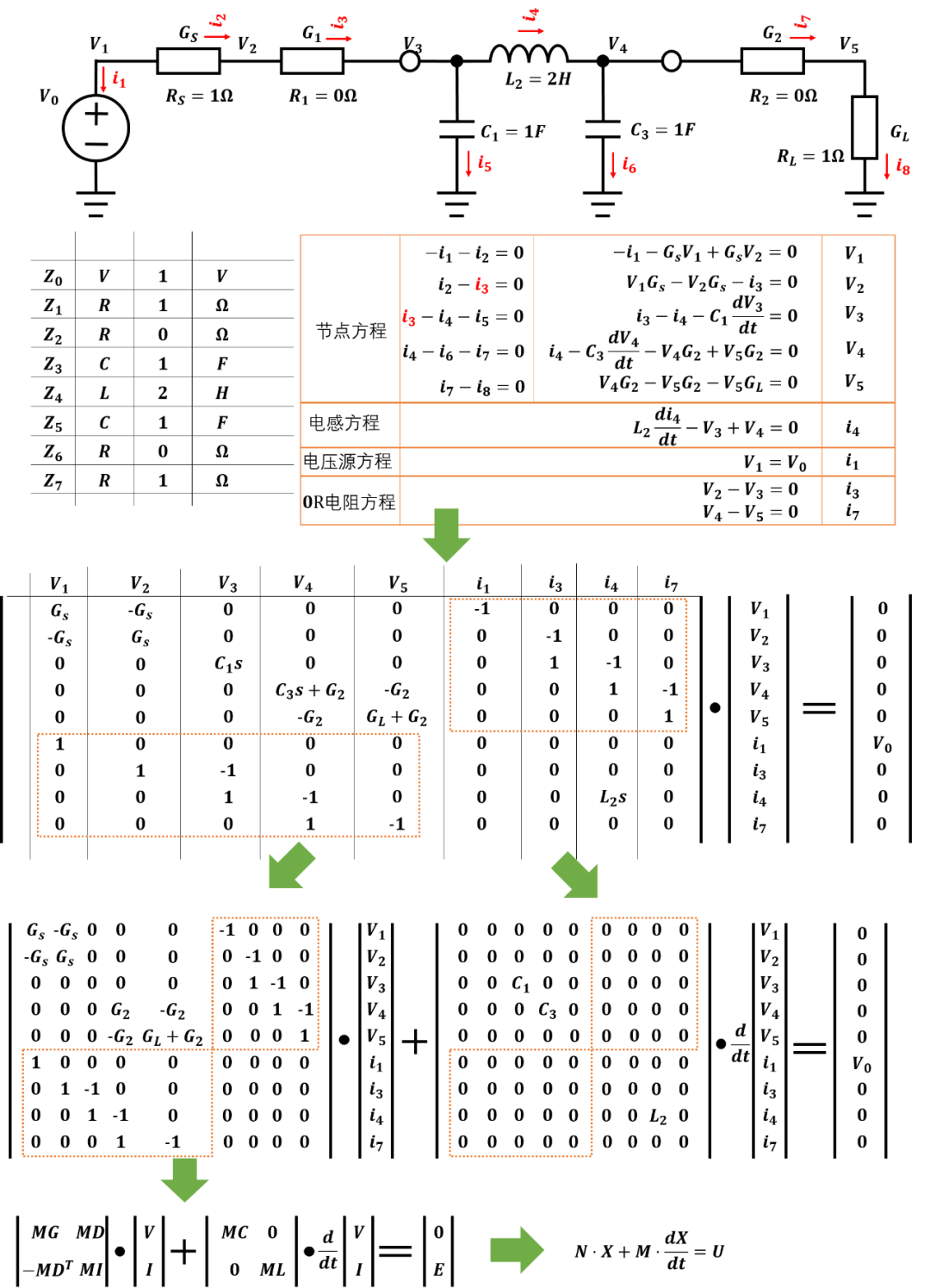
矩陣構建規則是:
當電阻??連接在vs和ve節點之間時,需要在??矩陣的(vs,vs)和(ve,ve)位置增加??,在N矩陣的(vs,ve)和(ve,vs)位置增加??。
當電阻??連接在vs和GND節點之間時,只需要在??矩陣的(vs,vs)位置增加??即可。
構建電流源支路的關聯矩陣??,設電流i所連接的節點是vs和ve時,規定電流vs到ve電流為正方向,那么在N矩陣中i所對應節點vs設置為1,在ve節點設置為-1。
當電路中存在電壓源時,定義電壓源電流??,關聯矩陣的??位置為1或-1,并且將E矩陣的??位置寫電壓源值。
當電路中存在電流源時,定義電流源電流??,在??矩陣的??位置寫1,并且將??矩陣??位置寫入電流源電流值。
矩陣構建規則是:
當電容??連接在vs和ve節點之間時,需要在??矩陣的(vs,vs)和(ve,ve)位置增加??,在??矩陣(vs,ve)和(ve,vs)位置增加??。
當電容??連接在vs和??節點之間時,只需要在??矩陣的(vs,vs)位置增加??即可。
當電感??的電流定義為i時,則需要在??矩陣的(i,i)位置設置為??。
矩陣??和??構造完成后,可以用后向歐拉法(Backward Euler method, BE)解微分方程求得瞬態特性。? 式中??是步進,所以??:?用此公式可以計算出瞬態值??,下圖就是之前的3階數巴特沃斯濾波器的瞬態響應曲線。
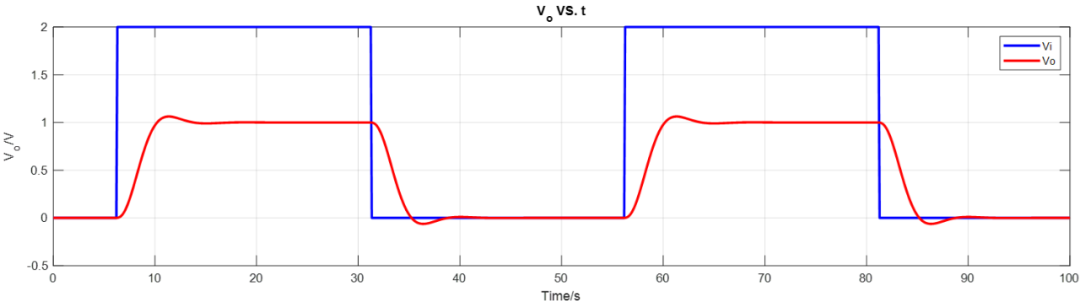
使用公式可以計算AC特性?下圖就是之前的3階數巴特沃斯濾波器的AC頻率響應曲線。
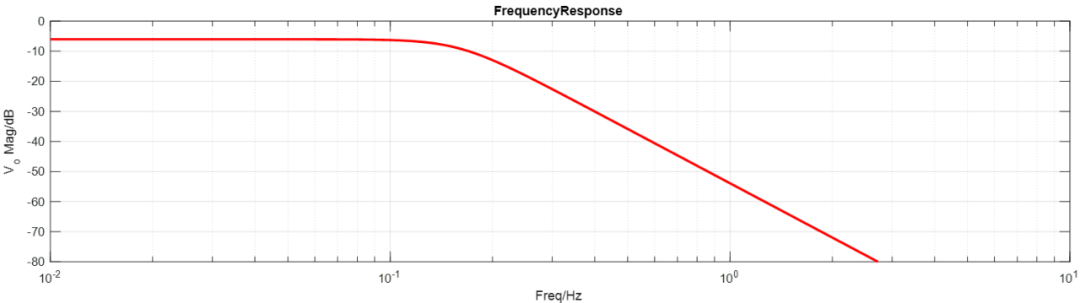
無源電路網絡原理圖構建
無源電路網絡原理圖構建可以將抽象的網表文件轉換為形象的原理圖,便于分析和理解。原理圖的構建本質上是一個圖論問題,如何在平面內將圖的枝節有意義的展示出來。這里分別討論了兩種不同的原理圖生成策略: 策略一 使用最長路徑構建原理圖(這里采用圖論算法中的深度搜索(圖的存儲,董曉算法)+回溯算法實現,實際上是解一個NP完全問題,有興趣的可以搜索哈密頓回路問題,Hamiltonian path problem??一道題難倒百萬人?一筆畫問題與哈密頓問題該怎么解?)。 本例子使用了比較復雜的例子用以比較不同策略的計算結果。
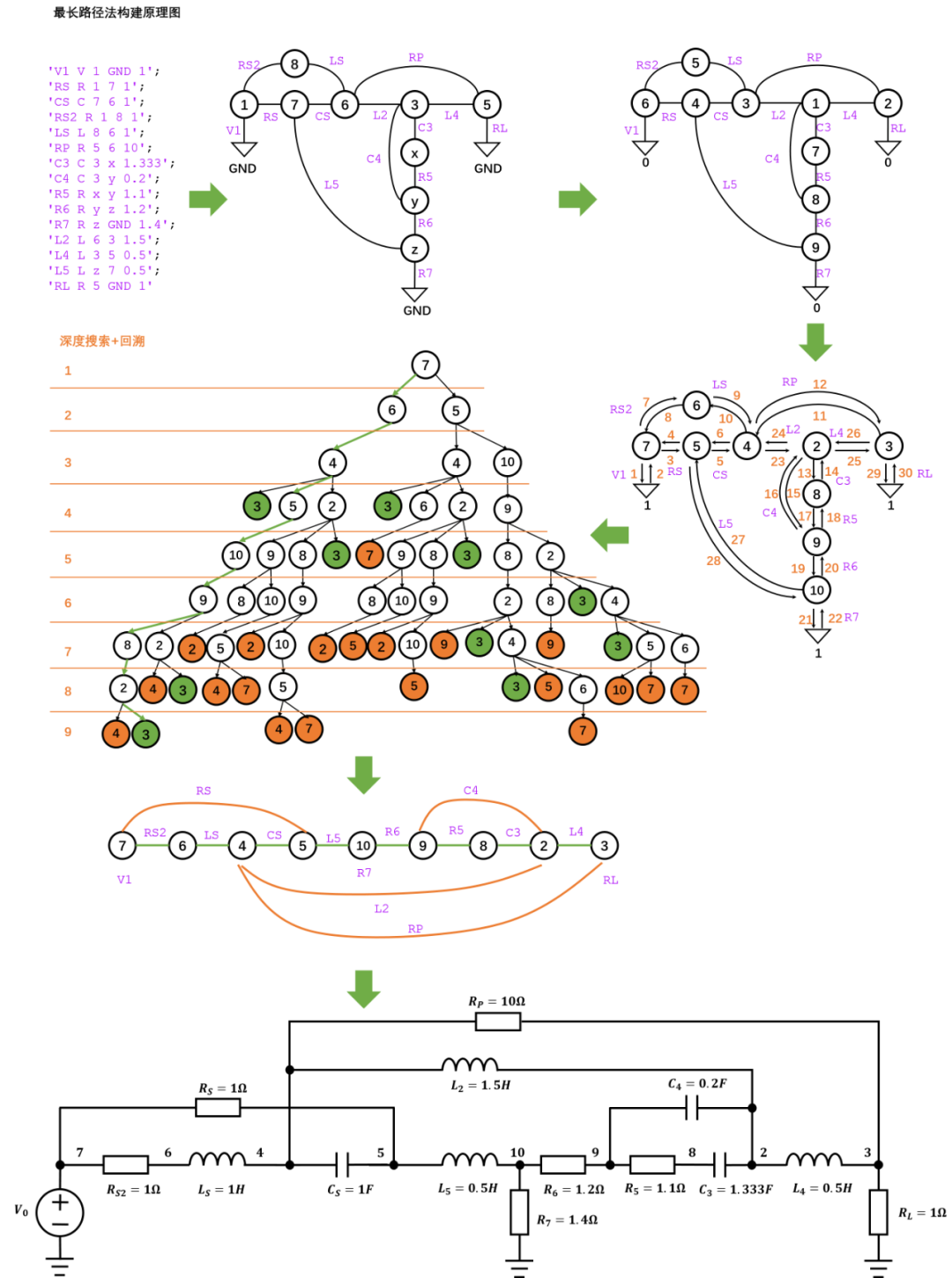
策略二 使用給定頻率點??的最小阻抗路徑構建原理圖(這里使用Dijkstra求最小路徑算法實現)。
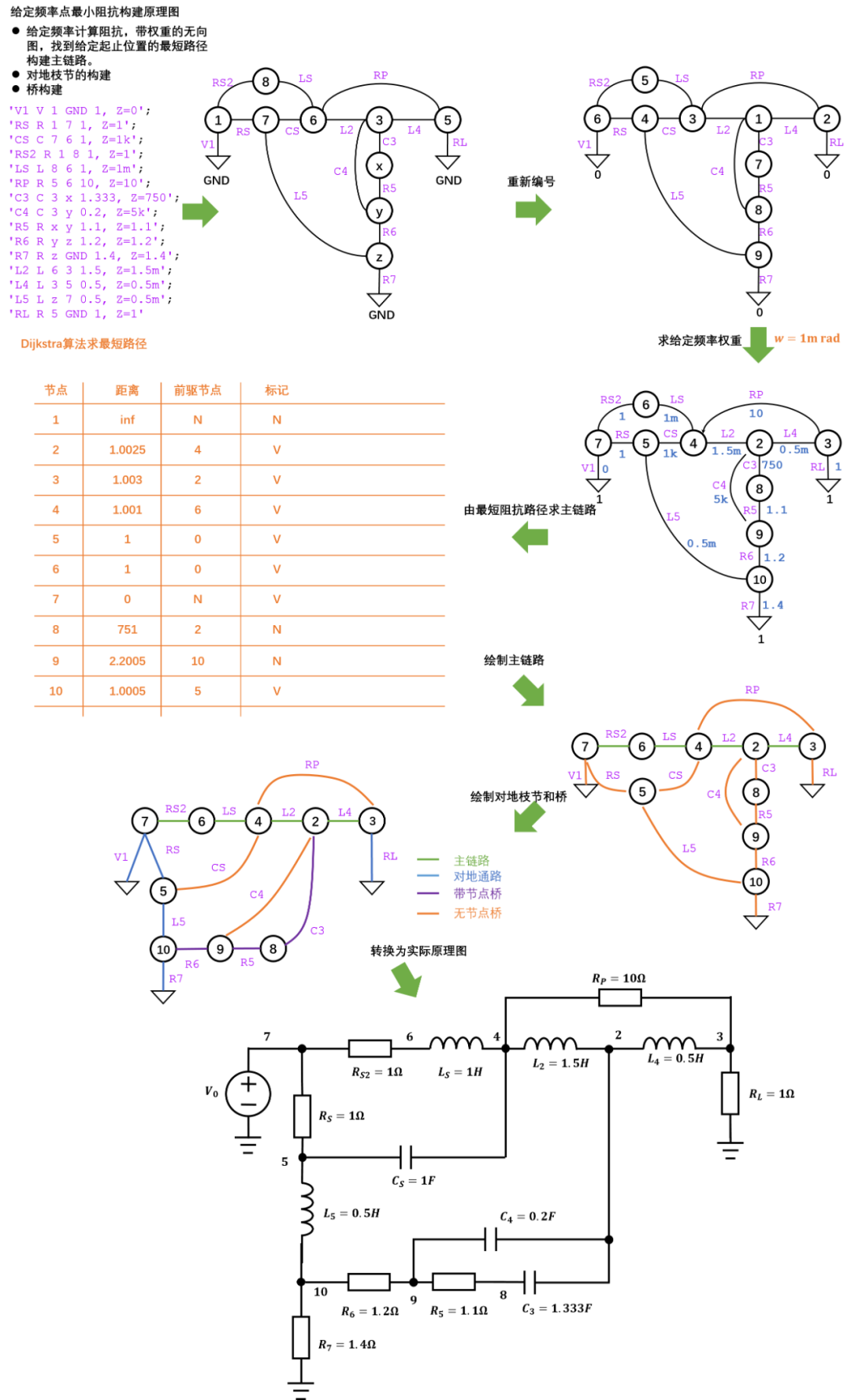
最終效果可以看出策略二所構建出來的原理圖比較容易讀懂,后續電路設計軟件中將采用第二種方法生成原理圖,對于濾波器設計,所有給定的原理圖構建頻率??需要在其通帶范圍內。 ? 原理圖構建采用前述策略二:
由給定??求出從源到負載的最短路徑(MainPath)
由MainPath各個節點出發到??的路徑(Branch2GNDPath)
由前兩種路徑節點(或橋)為起點和終點所構成的包含節點的橋(WiNodeBridge)
剩下的則為無節點橋(WoNodeBridge)
通過以上策略即可完成構建整個原理圖 ?
無源電路網絡仿真引擎
無源電路網絡仿真引擎采用Matlab編程,主要分為3大模塊:
原理圖構建模塊
AC仿真模塊
瞬態仿真模塊
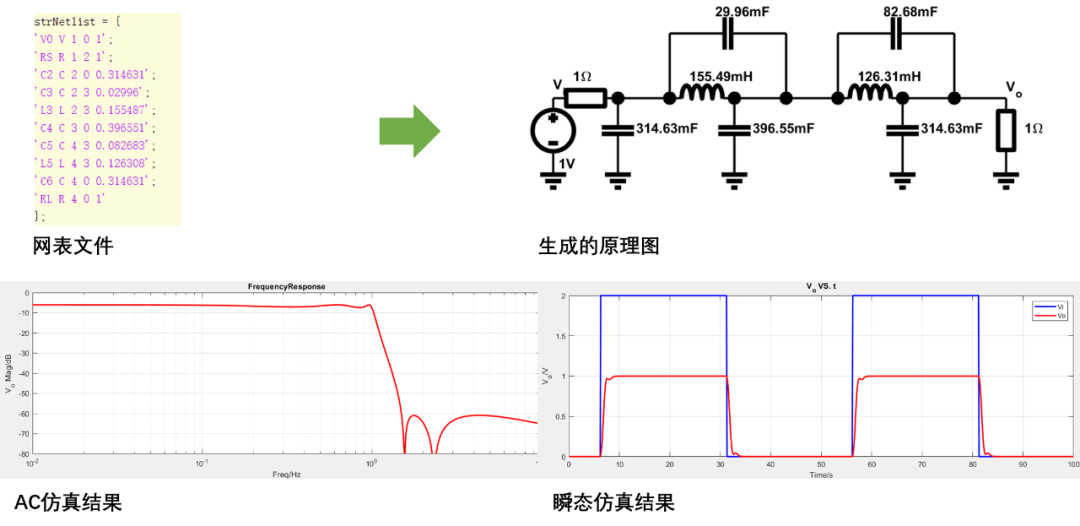
5階橢圓低通濾波器仿真
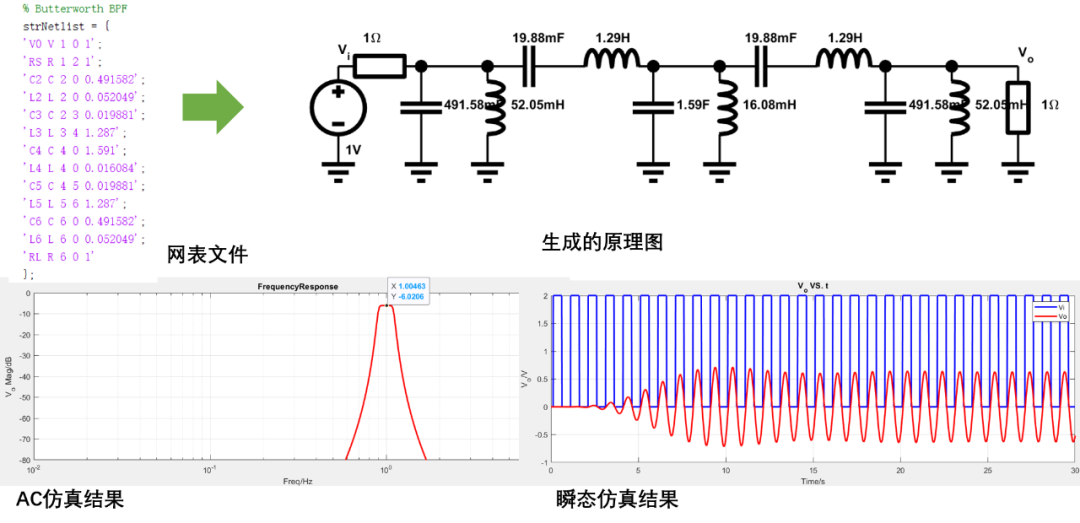
5階巴特沃斯帶通濾波器仿真(設計的濾波器中心頻率為1Hz,瞬態給定的是頻率為1Hz的方波信號。PS:瞬態仿真中步進需要取小些)
使用Spectre仿真器對上述帶通濾波器進行仿真
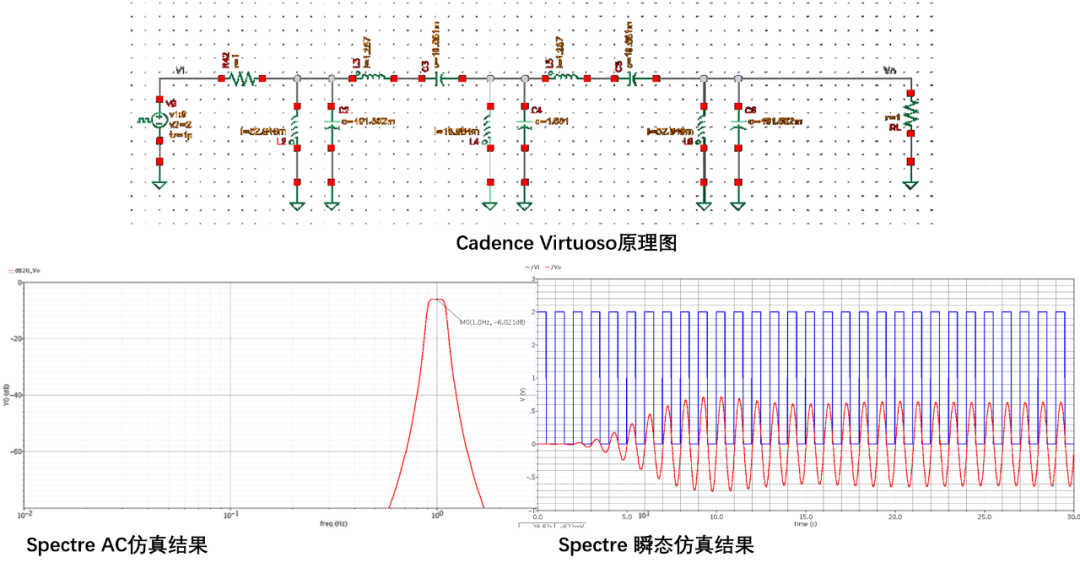
仿真結果對比:
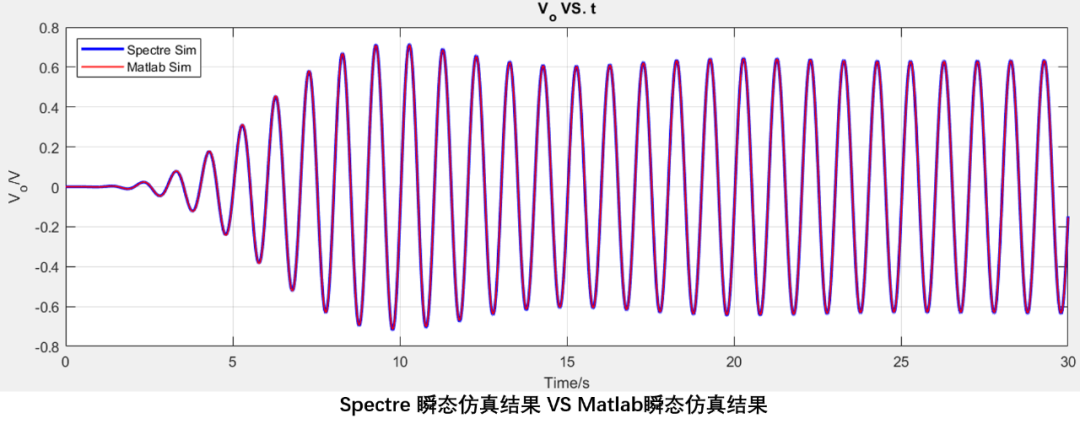
從圖中可以看到,Matlab仿真結果和Spectre仿真結果基本一致。 源碼見??: https://github.com/etools361/LadderNetworkSimEngine.git ?
? ? ? ?審核編輯 :李倩
?
?
 電子發燒友App
電子發燒友App












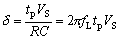











評論