本文分享串聯電路、并聯電路、混聯電路分析、計算方面的知識,通過學習串聯電路、并聯電路、混聯電路分析計算方面的知識,可以進一步掌握歐姆定律、電流、電壓、電阻的基本概念,學會解決實際工作中所遇到的電路方面的一些簡單問題。
一、串聯電路分析
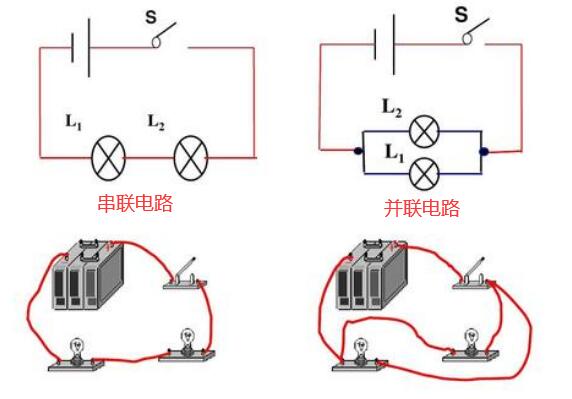
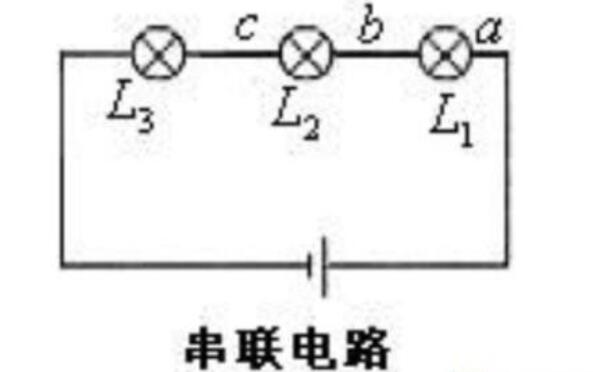
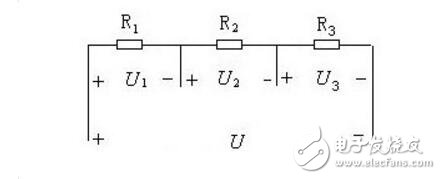
電阻的串聯連接,就是將兩個或兩個以上的電阻依次首尾順序連接,中間沒有其它分支電路,只有一條通路。如下圖所示的電路中,電阻 R1、R2、R3依次連接,形成串聯關系,再連接到電源U上。
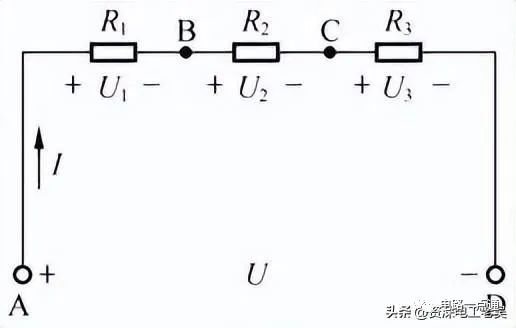
電阻串聯電路1、電阻串聯電路特點
(1)電阻串聯電路電流
由于沒有其它支路分流電流,所以,串聯電路中流過每個電阻的電流是相等的,即:
I=I1=I2=I3
這就像一條沒有支流的河流,在這條河流的每個位置,其流量是一樣的。實際電路中,可以通過使用萬用表的電流擋分別測量A、B、C、D各點的電流,其結果肯定是和上述完全一致。
(2)電阻串聯電路電壓
在串聯電路的總電壓,是各個電阻上的分電壓之和,即:
U=U1+U2+U3
使用萬用表電壓擋分別測量AB、BC、CD和AD之間的電壓,可以驗證該結論成立。
(3)電阻串聯電路電阻
將U=U1+U2+U3的兩邊都除以電流I,可得:
U/I=U1/I+U2/I+U3/I
由于I=I1=I2=I3,因此:U/I=U1/I+U2/I+U3/I=U1/I1+U2/I2+U3/I3
根據歐姆定律,U/I=R、U1/I1=R1、U2/I2=R2、U3/I3=R3,因此:
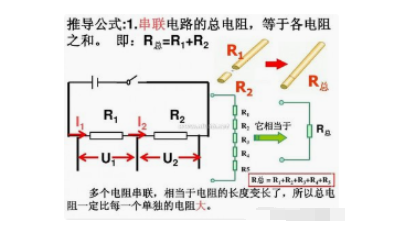
R=R1+R2+R3
即電路的總電阻R(等效電阻),則等于各串聯電阻(R1、R2、R3)之和。R稱做R1、R2、R3串聯的等效電阻。如下圖所示,在進行電路分析時,常用等效電阻來替代一組相互連接的電阻,以利于簡化電路、方便計算。
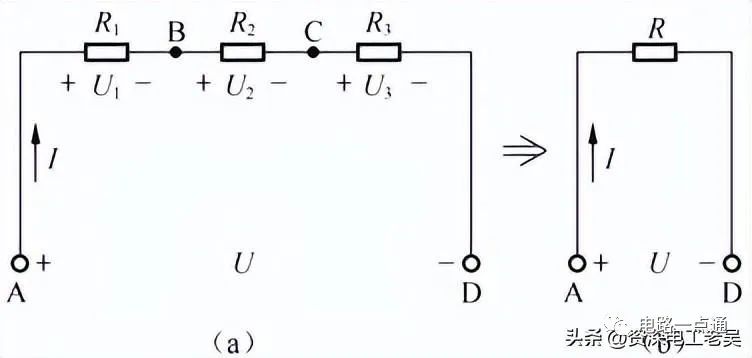
串聯電阻及其等效
通常電阻R1、R2…Rn串聯后的等效電阻可以記作R=R1+ R2+…+Rn。
電阻的串聯就好比是幾根水管連接在一起,每根水管就像是電阻,幾根水管連接在一起,水流是從同一根水管流出,水流大小不變,只不過是水管的總長度增加了,是每根水管長度之和。
(4)電阻串聯電路的功率
將U=U1+U2+U3同乘以電流I,得:UI=U1I+U2I+U3I
由于I=I1=I2=I3、UI=PU、U1I=P1、U2I=P2、U3I=P3
因此:P=P1+P2+P3
所以可得: 串聯電阻的總功率等于各電阻的分功率之和。
(5)電阻串聯電路的電壓分配
由于I=I1=I2=I3、I=U/R、I1=U1/R1、I2=U2/R2、I3=U3/R3
所以:I=U/R=U1/R1=U2/R2=U3/R3,
即:串聯電路中各電阻兩端的電壓與各電阻的阻值成正比,電阻越大,分配的電壓越大;電阻越小,分配的電壓也越小。
如果是兩個電阻R1和R2串聯,I=I1=I2、U/(R1+R2)=U1/R1=U2/R2,則:

上述就是兩個電阻R1和R2串聯后的分壓公式。
我們可以推導n個電阻串聯的電路中,第i個電阻兩端的電壓為:
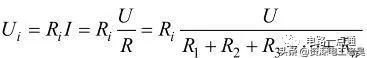
通常把上述公式稱為電阻串聯的分壓公式。
(6)電阻串聯電路的功率分配
由于I=I1=I2=I3,所以:
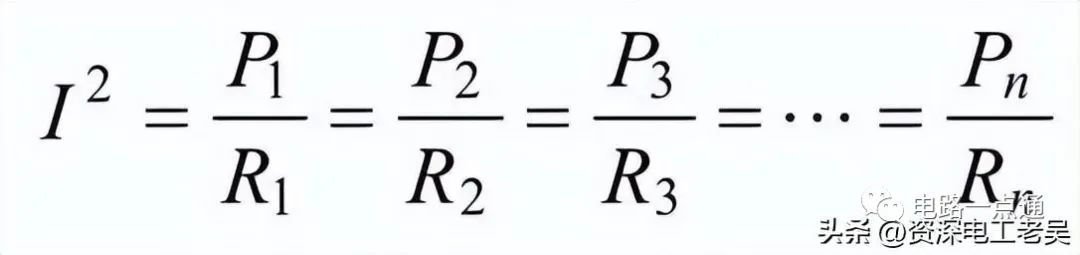
即串聯電路中各電阻消耗的功率與各電阻的阻值成正比。
2、電阻串聯電路分析、計算實例
【例1】在下圖中,已知流經電阻 R1的電流為 I1=3A,試說明流經電阻 R2的電流 I2為多少?
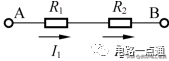
解:根據串聯電路中電流處處相等得,I1=I2=3A。
【例2】下圖所示的電阻串聯電路中,已知R1=2Ω,R2=3Ω,U2=6V,U=20V。求:(1)電路中的電流I;(2)R1和R3兩端的電壓;(3)電阻R3;(4)等效電阻R。

解:(1)根據歐姆定律,有I2=U2/R2=6/3=2A
因為是電阻串聯電路,所以I=I2=2A
(2)R1兩端的電壓U1=R1I1=R1I=2*2=4V
因為U=U1+U2+U3,所以R3兩端的電壓U3=U-U1-U2=20-4-6=10V
電阻R3=U3/I3=10/2=5Ω
等效電阻R=R1+R2+R3=2+3+5=10Ω
【例3】下圖 所示是常見的分壓器電路。已知電路的輸入電壓 UAB為 220V,電位器R=200?,當電位器觸點在中間位置時,求輸出電壓UCD。
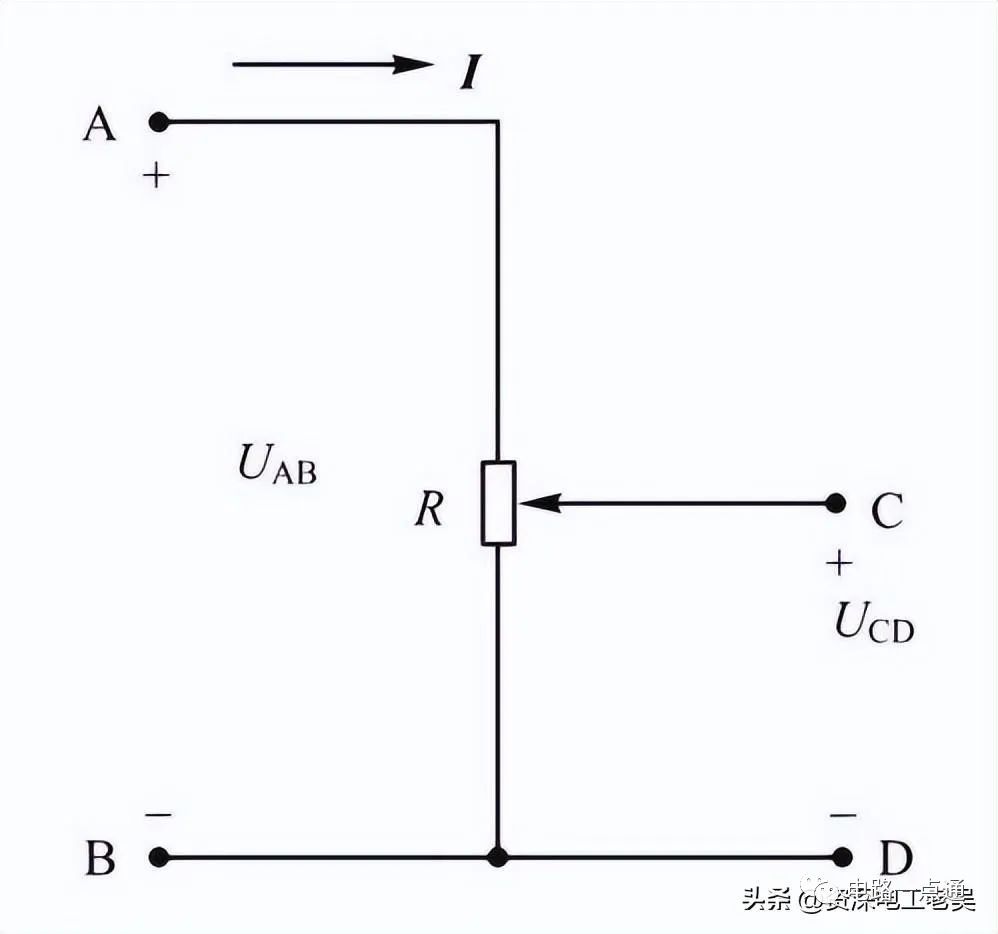
解:當電位器觸點在中間位置時,上、下電阻各為 100?,利用分壓公式即可求出輸出電壓,輸出電壓
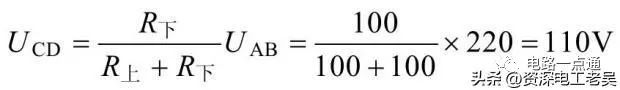
分壓器為電壓連續可調的分壓器,當電位器觸點上下移動時,輸出電壓UCD在0~UAB之間連續可調。
3、電阻串聯電路的應用
電阻串聯電路的應用十分廣泛。在工程上,常利用串聯電阻的方法來限制電路中的電流,如;常用的有電動機串電阻降壓啟動、電子電路中與二極管串聯的限流電阻等;也用串聯電阻的分壓作用來實現一定分壓要求,如用幾個電阻構成分壓器,使同一電源能供給不同的電壓;利用串聯電阻擴大電壓表的量程。
二、并聯電路分析
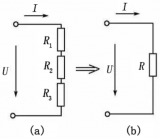
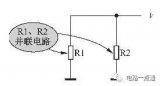
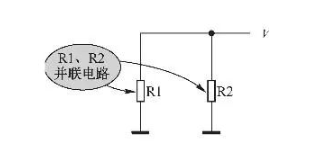
電阻的并聯是將若干個電阻的一端共同連接在電路的一點上,把它們的另一端共同連接在電路的另一點上,如下圖(a)所示,下圖(b)所示為其等效電路。
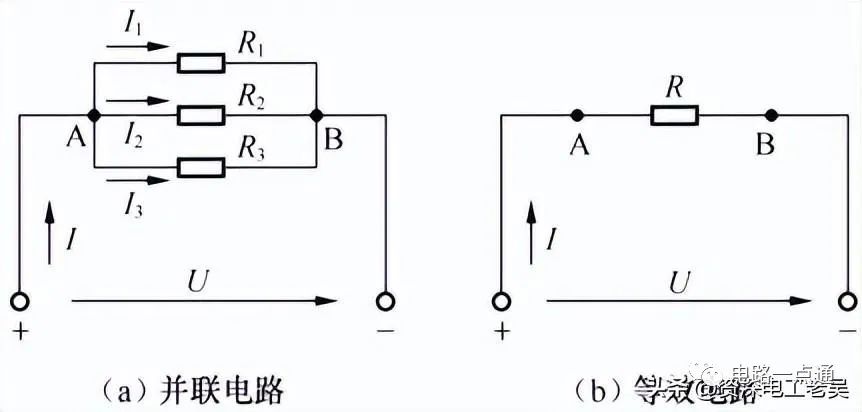
電阻并聯電路
1、電阻并聯電路特點
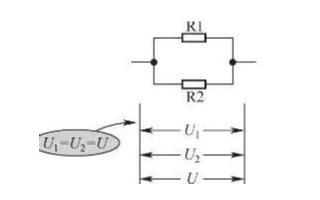
(1)電阻并聯電路電壓
由電阻并聯的連接方式可以看出,所有并聯電阻首端的電位相同、末端的電位也相同,所以并聯電阻兩端的電壓(即電位差)相等。上圖中,電阻R1、R2、R3兩端的電壓U1、U2、U3的關系為:
U1=U2=U3=U
(2)電阻并聯電路電流
我們可以用萬用表的電流擋分別測量通過電阻R1、R2、R3的電流I1、I2、I3以及干路電流I,可以得到:
I=I1+I2+I3
n個電阻并聯的電路中流經第i個電阻的電流為
Ii=U/Ri
上這個公式可以看出:流過各并聯電阻的電流與其阻值成反比,即阻值越大的電阻分配到的電流越小,阻值越小的電阻分配到的電流越大,這就是并聯電路的分流原理,通常把上式叫做電阻并聯的分流公式。
(3)電阻并聯電路電阻
由上圖中。可以看出:
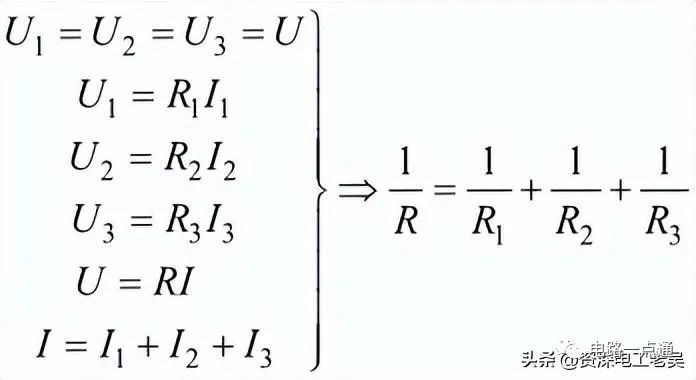
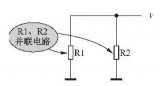
即并聯電路的總電阻(等效電阻)的倒數等于各電阻的倒數之和。
通常電阻R1和R2并聯后的等效電阻可以記作R=R1//R2。
當n個等值電阻R0并聯時,其等效電阻為:
R=R0/n。
當二個電阻R1R2并 聯時,其等效電阻為:
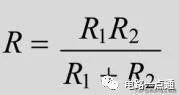
電阻的阻值越并越小,就好比是將幾根水管并排在一起,這幾根水管并排在一起,相當于各水管的水流疊加在一起,總的水流變大,水管阻礙水流的程度變小了。
(4)電阻并聯電路功率
將I=I1+I2+I3同乘以電壓U,得:UI=UI1+UI2+UI3,由于U1=U2=U3=U
所以根據功率定律,可得P=P1+P2+P3
即并聯電阻的總功率等于各電阻的分功率之和,這是串聯與并聯電路唯一相同之處,這也是因為能量總是守恒的,與電路的連接方式無關。
(5)電阻并聯電路電流分配
由于U1=U2=U3=U,所以:
U=R1I1=R2I2=R3I3=IR
即電路中通過各個電阻的電流,與各個電阻的阻值成反比。
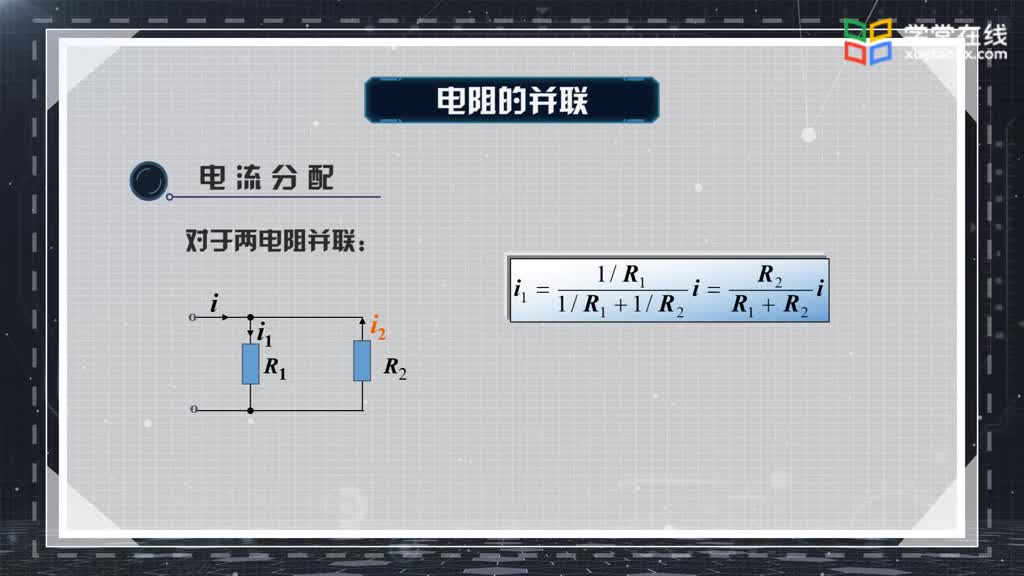
如果是兩個電阻R1和R2并聯,每個電阻所通過的電流為:
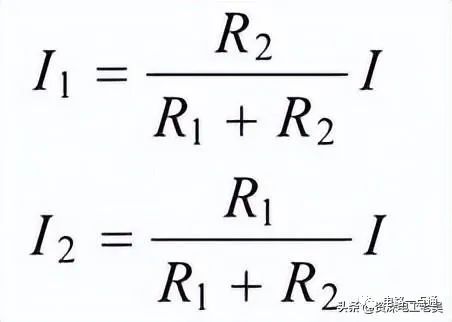
(6)電阻并聯電路功率分配
由于U=U1=U2=U3
所以:
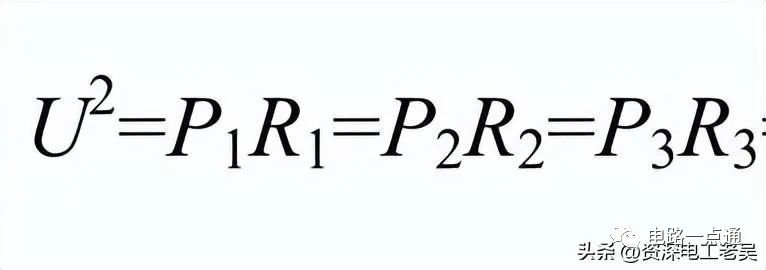
即并聯電路中通過各個電阻消耗的功率與各個電阻的阻值成反比。
2、電阻并聯電路分析、計算實例
【例1】有一個1000Ω的電阻,分別與10Ω、1000Ω、1100Ω的電阻并聯,并聯后的等效電阻各為多少?
解:并聯后的等效電阻分別為
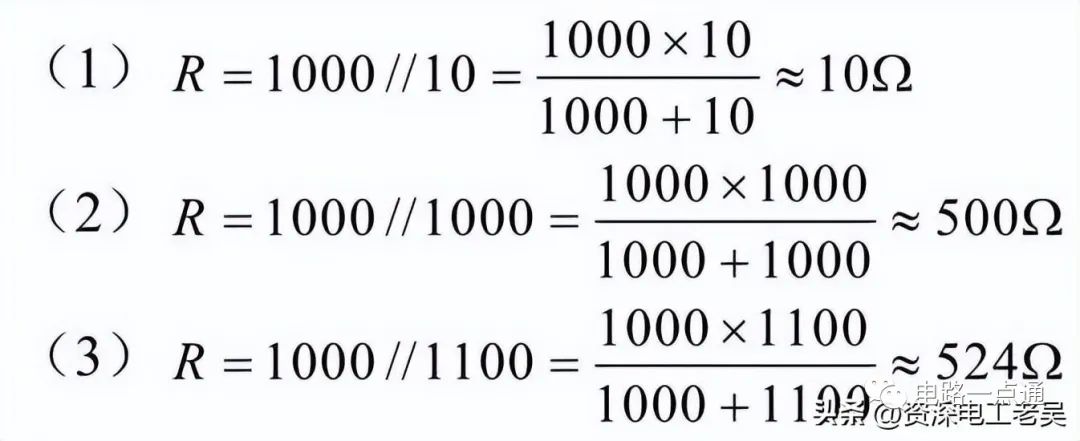
【例2】有2個白熾燈,它們的額定電壓都是220V,A燈的額定功率為40W,B燈額定功率為100W,電源電壓為220V。(1)將它們并聯連接時,白熾燈的電阻分別為多少?它們能正常工作嗎?功率分別為多少?哪一盞燈亮?(2)將它們串聯連接時,白熾燈的電阻分別為多少?它們能正常工作嗎?實際功率分別為多少?哪一盞燈亮?
解:無論是串聯還是并聯,白熾燈的電阻是不變的,首先計算燈泡的電阻
(1)白熾燈并聯時,白熾燈的電阻分別為:
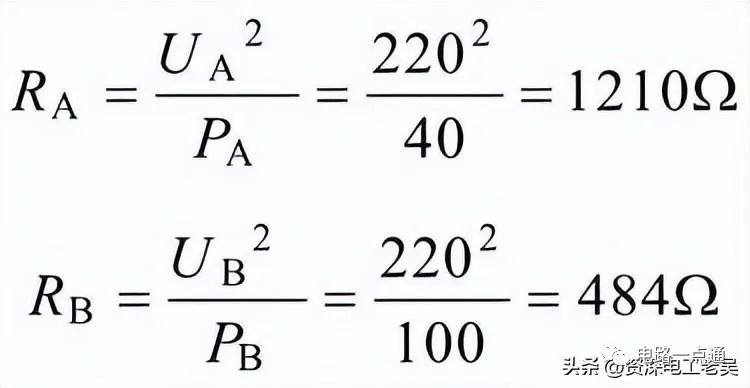
因為白熾燈在額定電壓下工作,所以白熾燈并聯時能正常工作,其功率分別為其額定功率,即40W和100W,100W的B燈亮。
(2)白熾燈串聯時,白熾燈的電阻不變,仍為RA=1210?,RB=484?,二個白熾燈的電壓分別為:
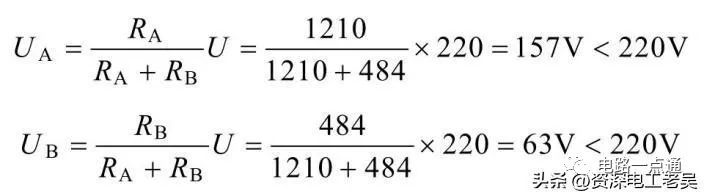
白熾燈的實際功率分別為:

因為白熾燈在串聯時,不是在額定電壓下工作,所以白熾燈串聯時不能正常工作,其實際功率分別為20.4W和8.2W,A燈亮。
3、電阻并聯電路的應用
電阻并聯電路的應用十分廣泛。在工程上,常利用并聯電阻的分流作用來實現一定要求,如利用并聯電阻擴大電流表的量程。同時,額定電壓相同的負載幾乎都采用并聯,這樣,既可以保證用電器在額定電壓下正常工作,又能在斷開或閉合某個用電器時,不影響其他用電器的正常工作。
三、混聯電路的分析
在實際應用中,電路中的電阻,大多不是單純的串聯或并聯,而是既有串聯又有并聯,這種既有串聯又有并聯的連接方式叫做電阻的混聯,如下圖所示。
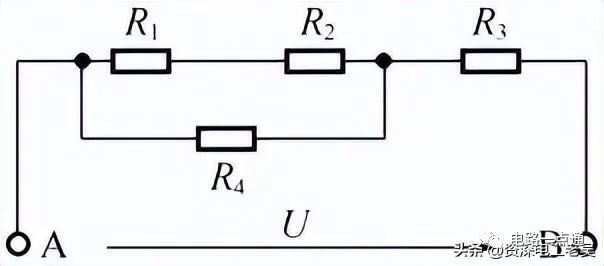
電阻混聯電路
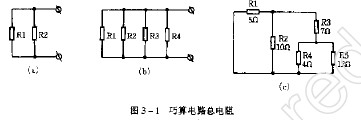
對混聯電路,有的比較直觀,可以直接看出各電阻之間的串、并聯關系,如上圖中為R1與R2串聯后與R4并聯,再與R3串聯的電路,則其等效電阻可以寫為:
R=(R1+R2)//R4+R3
【例1】如上圖所示的電阻混聯電路中,已知R1=R2=2Ω,R3=4Ω,R4=4Ω,求等效電阻R。
解:R=(R1+R2)//R4+R3=(2+2)//4+4=4//4+4=6Ω
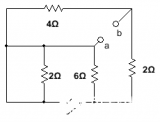
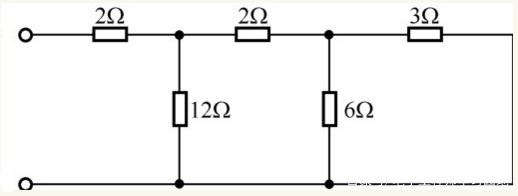
有的電路則比較復雜,不能直接看出各電阻之間的串、并聯關系,如下圖所示為電阻混聯電路,可以按照以下步驟操作。
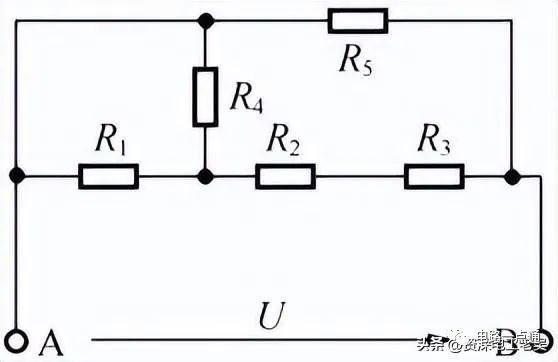
復雜的電阻混聯電路
① 將混聯電阻分解成若干個電阻的串聯、并聯,根據串并聯的特點進行計算,分別求出它們的等效電阻。
② 用求出的等效電阻取代電路中的串聯、并聯電阻,得到混聯電路的等效電路。
③ 若等效電路中仍是混聯電路,繼續按照步驟②化簡,以得到不含支路的等效電路。
④ 根據歐姆定律、串聯電路、并聯電路的特點列方程進行計算。
【例2】上圖所示的電阻混聯電路,已知R1=R4=4Ω,R2=R3=1Ω,R5=4Ω ,求等效電阻R
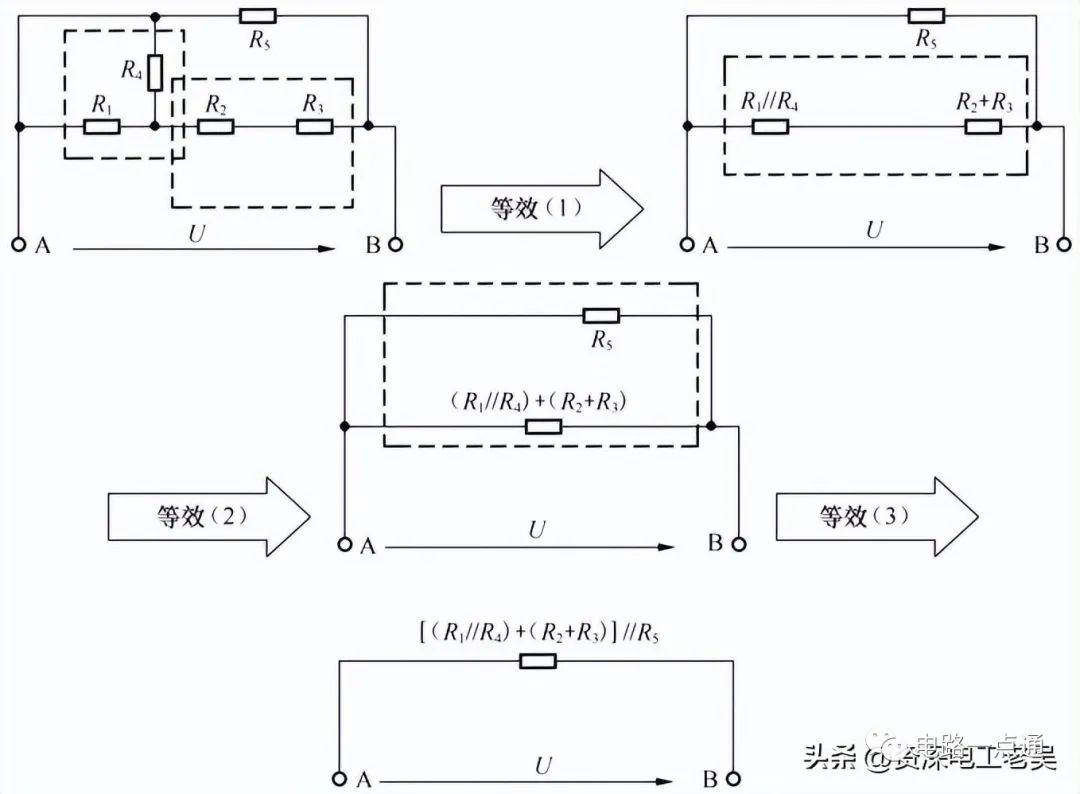
混聯電路的等效變換
解:(1)R1與R4為并聯,其等效電阻R′=R1//R4,
R′=R1R4/(R1+R4)=4*4/(4+4)=2Ω;
(2)R2與R3為串聯,其等效電阻R″=R2+R3,R″=1+1=2Ω。
(3)R′與R″為串聯,其等效電阻為R’’’=R′+ R″=2 + 2=4Ω。
(4)R5與R’’’為并聯,總電阻R=R5R’’’/(R5+R’’’)=4*4/(4+4)=2Ω
即:總的等效電阻為R=[ ( R1//R4)+( R2+R3) ]//R5,帶入得R=2Ω。
審核編輯:湯梓紅
?
 電子發燒友App
電子發燒友App




















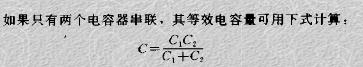










評論