預測控制中的穩態優化策略

??? 摘? 要：預測控制算法為了在自由度不足時按優先級優先保證基本控制目標，在自由度多余時充分利用自由度提高效益，在算法中引入了優化+控制的策略。本文首先介紹和分析了以前對預測控制的改進工作，最后給出了基于目標規劃思想的優化策略。
??? 關鍵詞：預測控制? 穩態優化? 目標規劃

1 引言
??? 預測控制算法除了可以處理約束外，吸引工程人員的另一個優點在于：作為一個多變量控制算法，預測控制中的系統輸入并不是僅僅和某一個特定的輸出關聯，所有的被控變量在一個體系之中。這樣就可以在系統由于輸入飽和、執行機構失靈等原因造成自由度丟失后，仍可以尋找最佳控制效果，保證裝置的平穩運行；另外如果存在多余的自由度，即在滿足控制要求的同時操縱變量可以在一定的范圍變化，這樣預測控制可以在更加經濟的狀態運行。但是傳統的控制策略不能夠實現上面的要求。
??? 為了發揮預測控制的優點，實現上面要求，需要引入新的策略。優化+控制策略是其中比較成功的策略之一，在優化層完成控制層的設定值計算，這一計算包括：按優先級首先確保重點控制目標，然后是一般控制目標，最后如果仍存在多余自由度，則在保證前面控制目標的前提下進行經濟優化。
??? 本文在對以前所做工作進行分析后，提出了基于目標規劃理論的優化策略，這種優化策略和傳統的算法相結合可以高效、簡潔地達到上面的目的。
2 以前的工作
??? 對R維輸入、S維輸出的系統，預測控制算法總是試圖求解未來M個時刻(控制時域)的控制，使模型預測輸出在未來P個時刻(優化時域)內達到以上基本目標。最初的動態矩陣控制(DMC)可以描述如下［１］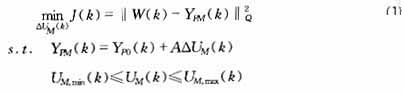

??????? (還包括一些其它變量，如被控變量、操縱變量的約束條件)???? (2)
??? 其中，W(k)為參考軌跡，(S×P)維向量；YPM(k)為ΔUM（k)作用下模型預測輸出，(S×P)維向量；YP0(k)輸出預測初值，(S×P)維向量；A為動態矩陣，由階躍響應系數排成的(S×P)×(R×M)維矩陣；Q=block-diag(Q1，…，Qs)，Qi=diag［qi(1),…,q?i(p)］,i=1,…,S。
??? 預測控制器的操縱變量多于被控變量時，操縱變量可能存在多余的自由度。充分利用多余自由度，預測控制可以在更經濟的狀態下運行。為了利用多余自由度，需要在控制目標中引入和經濟效益相關的變量，這些變量稱為經濟變量，可以歸結為控制量的穩態目標，如讓控制量盡量接近其理想穩態值(Ideal Rest Value-IRV)。
??? 基于這樣的思路將反映穩態優化要求的項加入到性能指標(1)中，就可以得到一種稱為綜合性能指標法的預測控制改進方法：


??? 但綜合性能指標法也存在缺點，具體如下［２］：（1)存在大的階躍擾動時，由于目標函數可能增加太快造成控制作用被抑制，使控制作用遲緩，輸出響應偏差大和回復時間長；（2)采用綜合指標法的控制系統一定是瘦系統，當存在模型失配和擾動時，設定值yset。和uset不可能同時實現。由于在實際中，模型失配和擾動的存在不可避免，這樣將造成穩態余差。

??? 其中等式約束中的YP′M′(k)是從未來P個時刻預測值中選出的。
??? 由于采用了分層優化的合理結構，多目標優化方法克服了綜合目標法的一些不足，但是這種方法對自由度減少和如何根據優先級，實現對主要控制目標的優先控制沒有涉及。這主要是由于改進算法把重點放在了如何利用“胖系統”的多余自由度上，沒有過多考慮“瘦系統”自由度不足時的情況。
??? Swartz［４］針對“瘦系統”自由度不足的情況，提出了分層監督控制策略，在監督控制中根據優先級，實現被控輸出設定值的優化計算。設定值通過根據優先級定義的優化子問題序列取得，其中每一個子問題都是一個二次規劃，其目標函數為盡可能使輸出設定值接近期望值而且在上一級優化子問題的約束，實現在保證上一級優化控制目標的前提下，進行優先級低的優化問題的求解。這種方法的優點：確保控制效果，采用分層的優化+控制結構。這種方法的缺點主要在于多級的二次規劃求解計算量太大，另外穩態經濟指標不能直接放入優化問題中，這樣在存在多余自由度的情況下，經濟目標的優化還需要其它工作。
??????? Swartz的監督控制策略中計算的是穩態時的輸出設定值，而經濟指標也是穩態優化，所以我們結合上面所做的工作，提出了一種新的優化+控制的兩級預測控制算法，同時實現穩態優化和動態控制。在優化部分使用簡單的目標規劃方法，提出了包括被控輸出設定值計算和經濟指標優化的穩態優化測量，在動態控制部分吸取綜合指標法的優點，增加了對穩態經濟目標的控制而且克服了綜合指標法的缺點。這種采用線性規劃進行局部優化、預測控制進行動態控制的算法，可以實現所謂胖瘦系統的自由轉換，在優先保證基本控制目標的前提下，實現經濟目標優化。
??? 總的來看，以前的工作都有可取之處，但是考慮的問題具有局限性，不是僅僅考慮了多自由度下的穩態經濟指標優化，就是僅僅考慮了自由度不足時基本控制目標的優先級控制。相比較而言，本文提出的改進的優化+控制策略可以實現胖瘦系統的自由轉變，而且在按優先級保證控制目標的前提下，追求經濟目標的最大化。
3 基于目標規劃的優化策略
??? 被控對象的線性穩態模型描述如下：
? ?Ｙ＝ＧＵ＋δ??? (4)
中G為穩態增益矩陣，δ是階躍擾動對輸出影響的估計。
??? δ提供了一種克服不可測擾動和模型失配影響的反饋機制，擾動估計可以采用?Cutler提出的方法，對于SISO系統：

??? 其中y(i)表示當前測量值，u和Δu分別為括號內采樣時刻的輸入和輸入變化，ai是單位階躍響應系數，N是系統的模型時域。假設擾動為階躍擾動。
??? 對于式(1)描述的系統，穩態優化的任務是根據約束和工程人員或者上一層優化給出的控制要求和期望的經濟指標，計算預測控制中的設定值。
??? 目標規劃［５］的目標函數是按各目標約束的正、負偏離變量和賦予相應的優先級系數而構造的，當每一個目標值確定以后，優化的要求是盡可能靠近目標值。優先級需要根據實際情況給出，設共有k個優先級，優先級系數Pi(i=1,2，…，k)滿足P1>>P2>>…，>>Pk。一般基本控制目標比經濟目標的優先級高主要控制目標比次要控制目標的優先級高。在實際應用中優先級系數只要保證優先級可以得到體現即可。
??? 如果是設定值優化那么目標函數是minz=f(d+,d-)，如果是不大于某一個區間上限則目標函數為minz=f(d＋)，如果是不小于某一個區間下限則目標函數為minz=f(d－)，如果是區間則控制目標為上面兩種情況的綜合。其中正偏差d＋表示決策值超過目標值的部分，負偏差d－表示決策值未達到目標值的部分，相關的d+、d-必定至少一個等于０。下面結合一個實例來說明基于目標規劃的穩態優化策略。
??? 例1［６］過程是由三個產品抽出和三個回流組成的重油分餾塔，塔底回流溫度是操作約束。操縱變量是塔頂和側線的抽出以及塔底的回流量。塔頂回流用來和其它裝置換熱，可以認為是可測擾動。4個輸出包括u3的理想穩態值，輸出輸入變量如表1。
??? 使用穩態增益并設那么穩態模型如式(3)描述，其中

??? 定義穩態優化目標以及優先級如表2

優化目標中-0．5＜y3屬于區間優化，y1＝0，y2=0屬于設定值優化，y4=0．5屬于經濟量的ESV。
硬約束為：－0．5≤y1≤0．5；－0．5≤ui≤0．5，i=1,2,3
這一優化問題的目標規劃如下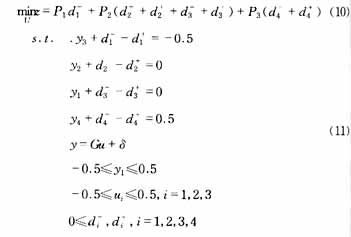

??? 計算結果控制作用為ul=0．5，u2=-0．0529，u3=-0．104。利用控制作用可以得到輸出的設定值yl=０、y2=0、y3=0．0076、y4=-0．104。也就是說預測控制中的設定值將從這幾個數據中產生。這樣的設定值是合理的，所以預測控制可以無偏的實現并且保證較快的回復時間。
??? 為了驗證目標規劃算法，假設前3個高優先級滿足那么這個問題可以用如下的線性規劃表示

??? 線性規劃的結果是-0．104，這也說明了目標規劃的正確性。如果有多余的自由度目標規劃也會把第4優化級優化到目標值，但是現在由于沒有多余的自由度，所以目標規劃就只有使第4優化級盡量接近目標值。
??? 例2

??? 情況1，當ytgt=5，IRV=0，解上述目標規劃可以得到動態控制的設定值為y=5；u2=0
??? 情況2，當ytgt=10，IRV=0，解上述目標規劃，由于ytgt=10的優先級高，所以首先滿足它，然后盡量減少u2的負偏差，結果為ul=3，u2=2。可以得到動態控制的設定值為y=5；u2=2。所謂胖瘦系統的轉變可以通過優化層變化控制層的設定值自然地得到體現。實際上由于沒有自由度，此時的經濟量為自然響應。
??? 情況3，當ytgt=15，IRV=0，解上述目標規劃，可以得到動態控制的設定值為y=12；u2=3。即使自由度用盡也不能夠滿足基本控制目標。
??? 情況4，當8≤ytgt≤10,IRV=0，經計算設定值為y=8；u2=1。y=8是為了在滿足區間的同時使經濟目標盡量接近IRV。
4 結論
??? 預測控制器的動態控制用于克服擾動保證最佳工作點和在最佳工作點變化后移動工作點，實現了控制器的調節特性和伺服特性。預測控制器的穩態優化則實時的根據擾動和工況的變化尋找最佳工作點，預測控制器中的穩態優化可以使預測控制器克服以前存在的缺點更平穩高效的運行。本文首先介紹了預測控制器的特點和以前所做的工作，最后給出了基于目標規劃理論的穩態優化策略。這種策略克服了傳統預測控制存在的不足，可在自由度不足時優先保證基本控制目標，在自由度多余時充分利用自由度提高效益，而且由于采用的線性規劃理論所以計算量不大。

參考文獻：

［１］肖明波，錢積新．預測控制中靜態目標的實現［Ｊ］．控制理論與應用，14(3)：313－317，1997
［２］Chao-Ming,srikanth Voorakaranam，Babu Joseph．Analysis and Performance of the LP-MPC and QP-MPC Cascade Control System［Ｃ］． Proceedings of the　ACC,Philadelphia,Pennsylvania．1998
［３］Grosdidier G.Froisy B．Hammann M.，The　IDCOM-M controller．IFAC Modelsbased predictive　process control［Ｃ］,1988，31－36
［４］C,L.E.Swartz,An algorithm for hierarchical supervisory control［Ｃ］．computers chem.eng.10(11):1173-1180(1995)