二進制分數使用與十進制數相同的加權原則,除了每個二進制數字使用base-2編號系統
我們知道十進制(或 denary )數字使用十進制(基數為10)編號系統,其中十進制數中的每個數字都允許采用0到9范圍內的十個可能值中的一個。因此,沿著十進制數從右向左移動,每個數字將它的值比其右邊的數字大十倍。
但是當我們從右向左移動時,每個數字都比前一個數字大十倍,每個數字也可以是當我們從左到右沿相反方向移動時,它比它的相鄰數字小十倍。
然而,一旦我們達到零(0)和小數點,我們不需要只停止,但可以繼續沿著數字從左到右移動,產生通常稱為分數。
典型的分數

這里以小數(或單數)數字為例,小數點右邊的數字(數字5)值為小數點左邊數字的十分之一(1/10或0.1)作為乘法值為1(1)的點(數字4)。
因此,當我們從左到右移動數字時,每個后續數字將立即成為數字值的十分之一
然后十進制編號系統使用位置或相對加權值的概念產生位置表示法,其中每個數字代表不同的加權值,取決于任何一側占據的位置小數點。
因此在標準的否定編號系統中數學上,這些值通常寫為:4 0 ,3 1 ,2 2 ,1 3 對于上面示例中小數點左邊的每個位置。同樣,對于小數點右邊的小數,數字的權重變得更負,給出:5 -1 ,6 -2 ,7 - 3 等。
因此我們可以看到標準十進制系統中的每個數字都表示該數字內該數字的大小或重量。那么任何十進制數的值將等于其數字的總和乘以它們各自的權重,因此對于上面的示例:加權小數中的 N = 1234.567 10 格式也是相同的:
1000 + 200 + 30 + 4 + 0.5 + 0.06 + 0.007 = 1234.567 10
或者可以編寫以反映每個否定數字的權重:
(1×1000)+(2×100)+(3×10)+(4×1)+( 5×0.1)+(6×0.01)+(7×0.001)= 1234.567 10
或甚至以多項式形式表示:
<跨度>(1×10 3 )+(2×10 2 )+(3×10 1 )+(4 ×10 0 )+(5×10 -1 )+(6×10 -2 )+(7×10 - 3 )= 1234.567 10
我們也可以使用這種位置表示法的概念,其中每個數字代表不同的加權值取決于它在二進制編號系統中占據的位置。這次的不同之處在于二進制數系統(或簡稱二進制數)是一個位置系統,其中數字的不同加權位置是2的冪(base-2)而不是10。
二進制分數
二進制編號系統是base-2編號系統,只包含兩個數字,“0”或“1”。因此,二進制數的每個數字可以取“0”或“1”值,其中0或1的位置表示其值或加權。但是我們也可以對小于1的值進行二進制加權,產生所謂的無符號小數二進制數。
與小數小數類似,二進制數也可以通過將二進制數放入到無符號小數中來表示小數點的右邊或在這種情況下,二進制點。因此,二進制點右側的所有小數位具有各自的權重,其為2的負冪,從而產生二進制分數。換句話說,2的冪是負的。
因此對于二進制點右邊的小數二進制數,每個數字的權重變得更負,給出:2 -1 ,2 -2 ,2 -3 ,2 -4 ,依此類推。
二進制分數
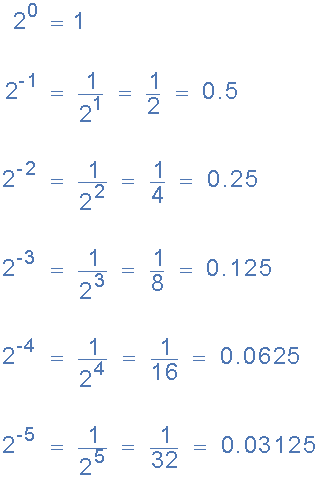
等等
因此,如果我們采用0.1011的二進制分數 2 然后考慮每個數字的位置權重,給出其十進制等值:
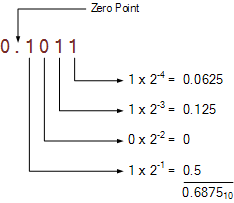
對于此示例,二進制數0.1011 2 的小數部分轉換為0.6875 10 。
二進制分數示例No1
現在假設我們有以下二進制數: 1101.0111 2 ,它的等效十進制數是多少。
<跨度> 1101.0111 =(1×2 3 )+(1×2 2 )+(0×2 1 )+(1×2 0 )+(0×2 -1 )+(1×2 -2 )+(1×2 -3 )+(1×2 -4 )
<跨度> = 8 + 4 + 0 + 1 + 0 + 1/4 + 1/8 +16分之1
<跨度> = 8 + 4 + 0 + 1 + 0 + 0.25 + 0.125 + 0.0625 = 13.4375 10
因此, 1101.0111 2 給出如下:13.4375 10
所以我們可以看到分數二進制數,即加權小于1的二進制數(2 0 ),可以通過將2的冪的每次減少的二進制加權因子連續除以2來轉換成它們的十進制數當量,同時記住2 0 等于1,
其他二元分數實例
0.11 =(1×2 -1 )+(1×2 - 2 )= 0.5 + 0.25 = 0.75 <子> 10
<跨度> 11.001 =(1×2 1 )+ (1×2 0 )+(1×2 -3 )= 2 + 1 + 0.125 = 3.125 <子> 10
<跨度> 1011.111 =(1×2 3 )+(1×2 1 )+(1×2 0 )(1×2 -1 )+(1×2 -2 )+(1×2 -3 )
=8+2+1+0.5+0.25+0.12 5 = 11.875 10
將十進制轉換為二進制分數
使用a將小數部分轉換為小數二進制數類似于我們用于整數的方法。但是,這個時間乘法用而不是用整數除法而不是用于進位數的余數是十進制數的小數部分的二進制等價。
當從十進制轉換為二進制時,整數(正序從右到左)部分和十進制數的小數(從左到右的部分)部分是單獨計算的。
對于數字的整數部分,二進制等價通過連續地將(稱為連續除法)十進制數的整數部分重復地除以2(÷2),從最低有效位(LSB)到最高有效位(MSB)以相反的順序記錄剩余部分,直到找到該值變為“0”,產生二進制等價。
所以要找到十進制整數的二進制等值: 118 10
118 (除以2)= 59plus余數0(LSB)
59 (除以2)= 29plus剩余nder1(↑)
29 (除以2)= 14plus余數1(↑)
14 (除以2)= 7plus余數0(↑ )
7 (除以2)= 3plus余數1(↑)
3 (除以2)= 1plus余數1(↑)
1 (除法by 2)= 0plus余數1(MSB)
然后二進制當量 118 10 因此: 1110110 2 ←(LSB)
通過連續乘法(稱為連續乘法)找到數字的小數部分將十進制數的小數部分重復2(×2),以正向順序記錄進位,直到該值變為“0”,產生二進制等價。
因此,如果乘法過程產生的產品更大如果乘法過程產生的產品小于“1”,則進位為“1”進位是“0”。
另請注意,如果連續的乘法過程似乎沒有朝向最終的零,則小數將具有無限長度或直到相等的位數已經獲得,例如8位。或者16位等等,具體取決于所需的精度。
所以要找到等效小數的二進制分數: 0.8125 10
0.8125 (乘以2)=1.625 = 0.625carry1( MSB)
0.625 (乘以2)=1.25 = 0.25carry1(↓)
0.25 (乘以2)=0.50 = 0.5carry0(↓)
0.5 (乘以2)=1.00 = 0.0carry1( LSB)
因此, 0.8125 10 的二進制當量是: 0.1101 2 ← (LSB)
我們可以使用上面的步驟仔細檢查這個答案,將二進制分數轉換成等效的十進制數: 0.1101 = 0.5 + 0.25 + 0.0625 = 0.8125 10
二進制分數示例No2
查找等效于以下十進制數的二進制分數: 54.6875
首先我們使用從上面的連續除法以正常方式將整數54轉換為二進制數。
54 (除以2)= 27remainder0(LSB)
27 (除以2)= 13remainder1(↑)
13 (除以2)= 6rem ainder1(↑)
6 (除以2)= 3remainder0(↑)
3 (除以2)= 1remainder1(↑)
1 (除以2)= 0remainder1(MSB)
因此二進制當量因此, 54 10 : 110110 2
接下來我們將小數部分轉換為0.6875使用連續乘法得到二進制分數。
0.6875 (乘以2)=1.375 = 0.375carry1(MSB)
0.375 (乘以2)=0.75 = 0.75carry0(↓)
0.75 (乘以2)=1.50 = 0.5carry1(↓)
0.5 (乘以2)=1.00 = 0.0carry1(LSB)
因此, 0.6875 10 的二進制等效值是: 0.1011 2 ←(LSB)
因此二進制等效的十進制數: 54.6875 10 是 110110.1011 2
二元分數摘要
我們在本教程中已經看到二元分數將任何小數部分轉換為等效的二進制分數,我們必須將小數部分乘以小數部分,并將小數部分乘以2并記錄數字出現在二進制點的左側。這個二進制數字是進位數字,總是為“0”或“1”。
然后我們必須將剩余的小數部分乘以2再次使用連續乘法重復上述序列直到分數對于重復的二進制分數,已經減少到零或者已經完成了所需的二進制位數量。分數由2的負冪表示。
對于混合十進制數,我們必須執行兩個單獨的運算。小數點左邊的整數部分的連續除法和小數點右邊的小數部分的連續乘法。
請注意,混合十進制數的整數部分將始終具有精確值二進制數等價,但小數部分可能不等,因為如果我們想要精確地表示小數部分,我們可以得到一個重復分數,產生無限數量的二進制數字。
-
二進制
+關注
關注
2文章
795瀏覽量
41719 -
十進制
+關注
關注
0文章
67瀏覽量
13252
發布評論請先 登錄
相關推薦




 二進制分數的使用
二進制分數的使用











評論