在本文中，作者對(duì)常用的三種機(jī)器學(xué)習(xí)優(yōu)化算法（牛頓法、梯度下降法、最速下降法）進(jìn)行了介紹和比較，并結(jié)合算法的數(shù)學(xué)原理和實(shí)際案例給出了優(yōu)化算法選擇的一些建議。

閱讀本文的基礎(chǔ)準(zhǔn)備

線性代數(shù)

多變量微積分

對(duì)凸函數(shù)的基本知識(shí)

我們都知道，機(jī)器學(xué)習(xí)中最重要的內(nèi)容之一就是優(yōu)化問題。因此，找到一個(gè)能夠?qū)瘮?shù)做合理優(yōu)化的算法始終是我們關(guān)注的問題。當(dāng)前，我們使用最多的優(yōu)化算法之一是梯度下降算法。在本文中，我們會(huì)對(duì)梯度下降算法以及一些其他的優(yōu)化算法進(jìn)行介紹，并嘗試從理論角度來理解它們。本文介紹的核心算法包括：

牛頓法（Newton’s Method）

最速下降法（Steep Descent）

梯度下降法（Gradient Descent）

如果想對(duì)這些算法有更多了解，你可以閱讀斯坦福大學(xué)的《凸函數(shù)優(yōu)化—：第三部分》教材。在本文中，我們主要關(guān)注二次函數(shù)和多項(xiàng)式函數(shù)。

對(duì)待優(yōu)化函數(shù)的基本假設(shè)

一般而言，我們假設(shè)我們處理的函數(shù)的導(dǎo)數(shù)都是連續(xù)的（例如，f ∈ C1）。對(duì)于牛頓法，我們還需要假設(shè)函數(shù)的二階導(dǎo)數(shù)也是連續(xù)的（例如， f ∈ C2）。最后，我們還需要假設(shè)需要最小化的函數(shù)是凸函數(shù)。這樣一來，如果我們的算法集中到一個(gè)點(diǎn)（一般稱為局部最小值），我們就可以保證這個(gè)值是一個(gè)全局最優(yōu)。

牛頓法

單變量函數(shù)的情況

x_n = starting pointx_n1 = x_n - (f'(x_n)/f''(x_n))while (f(x_n) != f(x_n1)): x_n = x_n1 x_n1 = x_n - (f'(x_n)/f''(x_n))

牛頓法的基本思想是，需要優(yōu)化的函數(shù)f在局部可以近似表示為一個(gè)二次函數(shù)。我們只需要找到這個(gè)二次函數(shù)的最小值，并將該點(diǎn)的x值記錄下來。之后重復(fù)這一步驟，直到最小值不再變化為止。

多變量函數(shù)的情況

對(duì)于單變量的情況，牛頓法比較可靠。但是在實(shí)際問題中，我們處理的單變量情形其實(shí)很少。大多數(shù)時(shí)候，我們需要優(yōu)化的函數(shù)都包含很多變量（例如，定義在實(shí)數(shù)集?n的函數(shù)）。因此，這里我們需要對(duì)多變量的情形進(jìn)行討論。

假設(shè)x∈ ?n，則有：

x_n = starting_pointx_n1 = x_n - inverse(hessian_matrix) (gradient(x_n))while (f(x_n) != f(x_n1)):x_n = x_n1x_n1=x_n-inverse(hessian_matrix)(gradient(x_n))

其中，gradient(x_n)是函數(shù)位于x_n點(diǎn)時(shí)的梯度向量，hessian_matrix是一個(gè)尺寸為 nxn 的黑塞矩陣（hessian matrix），其值是函數(shù)位于x_n的二階導(dǎo)數(shù)。我們都知道，矩陣轉(zhuǎn)換的算法復(fù)雜度是非常高的（O(n3)），因此牛頓法在這種情形下并不常用。

梯度下降

梯度下降是目前為止在機(jī)器學(xué)習(xí)和其他優(yōu)化問題中使用的最多的優(yōu)化算法。梯度算法的基本思想是，在每次迭代中向梯度方向走一小步。梯度算法還涉及一個(gè)恒定的alpha變量，該變量規(guī)定每次跨步的步長(zhǎng)。下面是算法示例：

alpha = small_constantx_n = starting_pointx_n1 = x_n - alpha * gradient(x_n)while (f(x_n) != f(x_n1)): # May take a long time to converge x_n = x_n1 x_n1 = x_n - alpha * gradient(x_n)

這里，alpha是在每次迭代中更新x_n時(shí)都需要使用的變量（一般稱為超參數(shù)）。下面我們對(duì)alpha值的選擇進(jìn)行簡(jiǎn)單分析。

如果我們選擇一個(gè)很大的alpha，我們很可能會(huì)越過最優(yōu)點(diǎn)，并離最優(yōu)點(diǎn)越來越遠(yuǎn)。事實(shí)上，如果alpha的值過大，我們甚至?xí)耆x最優(yōu)點(diǎn)。

當(dāng)alpha的值過大時(shí)，10次迭代后的梯度下降情況

另外，如果我們選擇的alpha值過小，則可能需要經(jīng)過非常多次迭代才能找到最優(yōu)值。并且，當(dāng)我們接近最優(yōu)值時(shí)，梯度會(huì)接近于0。因此 ，如果alpha的值過小，我們有可能永遠(yuǎn)都無法到達(dá)最優(yōu)點(diǎn)。

當(dāng)alpha的值過小時(shí)，10次迭代后的梯度下降情況

因此，我們可能需要多嘗試一些alpha的值，才能找到最優(yōu)的選擇。如果選擇了一個(gè)合適的alpha值，我們?cè)诘鷷r(shí)往往能節(jié)省很多時(shí)間。

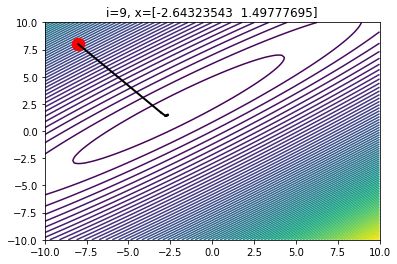
當(dāng)alpha的值合理時(shí)，10次迭代后的梯度下降情況

最速下降法

最速下降法和梯度下降法非常相似，但是最速下降法對(duì)每次迭代時(shí)要求步長(zhǎng)的值為最優(yōu)。下面是最速下降法的算法示例：

x_n = starting_pointalpha_k = get_optimizer(f(x_n - alpha * gradient(x_n)))x_n1 = x_n - alpha_n * gradient(x_n)while (f(x_n) != f(x_n1)): x_n = x_n1 alpha_k = get_optimizer(f(x_n - alpha * gradient(x_n))) x_n1 = x_n - alpha_n * gradient(x_n)

其中，x_n和x_n1是?n上的向量，是算法的輸入，gradient是函數(shù) f 在點(diǎn)x_n的梯度，alpha_k的數(shù)學(xué)表示如下：

因此，在對(duì)原始函數(shù)進(jìn)行優(yōu)化時(shí)，我們需要在每一次迭代中對(duì)一個(gè)內(nèi)部函數(shù)進(jìn)行優(yōu)化。這樣做的優(yōu)點(diǎn)是，這個(gè)內(nèi)部?jī)?yōu)化函數(shù)是一個(gè)單變量函數(shù)，它的優(yōu)化不會(huì)非常復(fù)雜（例如，我們可以使用牛頓法來作為這里的函數(shù)）。但是在更多情形下，在每一步中優(yōu)化這個(gè)函數(shù)都會(huì)帶來比較昂貴的花銷。

二次式函數(shù)的特殊情形

對(duì)于均方誤差函數(shù)：

其中，I是單位矩陣，y=Qw + b。為了簡(jiǎn)化討論，這里我們只考慮尋找權(quán)重w最優(yōu)值的情形（假設(shè)b是連續(xù)的）。將等式y(tǒng)=Qw + b帶入上式并進(jìn)行一定整理后，我們可以得到如下等式：

現(xiàn)在我們重新查看一下g(α)， 我們會(huì)發(fā)現(xiàn)，如果我們使用點(diǎn)αk處的梯度，由于其為最優(yōu)值，該梯度應(yīng)當(dāng)為0。因此我們有如下等式：

對(duì)上式進(jìn)行簡(jiǎn)化，并將f的梯度帶入后，我們可以得到對(duì)于αk的表示如下：

這就是在二次函數(shù)情形下αk的值。

對(duì)二次函數(shù)的收斂性分析

對(duì)于定義在?2上的二次函數(shù)，最速下降法一般用來在非常接近最優(yōu)值時(shí)使用，使用步數(shù)不超過十步。

二維中的最速下降在4次迭代后的情形

在上圖中，每一次迭代中的改變方向都是垂直的。在3到4次迭代后，我們可以發(fā)現(xiàn)導(dǎo)數(shù)的變化基本可以忽略不計(jì)了。

為什么最速下降法應(yīng)用很少？

最速下降法算法遠(yuǎn)遠(yuǎn)滿足了超參數(shù)調(diào)優(yōu)的需求，并且保證能找到局部最小值。但是為什么該算法應(yīng)用不多呢？最速下降法的問題在于，每一步都需要對(duì) aplha_k 進(jìn)行優(yōu)化，這樣做的成本相對(duì)高昂。

例如，對(duì)于二次函數(shù)，每次迭代都需要計(jì)算多次矩陣乘法以及向量點(diǎn)乘。但對(duì)于梯度下降，每一步只需要計(jì)算導(dǎo)數(shù)并更新值就可以了，這樣做的成本遠(yuǎn)遠(yuǎn)低于最速下降算法。

最速下降算法的另一個(gè)問題是對(duì)于非凸函數(shù)的優(yōu)化存在困難。對(duì)于非凸函數(shù)，aplha_k 可能沒有固定的值。

對(duì)于梯度下降法和最速下降法的對(duì)比

在這一部分，我們對(duì)梯度下降法和最速下降法進(jìn)行對(duì)比，并比較它們?cè)跁r(shí)間代價(jià)上的差異。首先，我們對(duì)比了兩種算法的時(shí)間花銷。我們會(huì)創(chuàng)建一個(gè)二次函數(shù)：f:?2???→?（該函數(shù)為一個(gè)2000x2000的矩陣）。我們將對(duì)該函數(shù)進(jìn)行優(yōu)化，并限制迭代次數(shù)為1000次。之后，我們會(huì)對(duì)兩種算法的時(shí)間花銷進(jìn)行對(duì)比，并查看 x_n 值與最優(yōu)點(diǎn)的距離。

我們先來看一下最速下降法：

0 Diff: 117727672.56583363 alpha value: 8.032725864804974e-06 100 Diff: 9264.791000127792 alpha value: 1.0176428564615889e-05 200 Diff: 1641.154644548893 alpha value: 1.0236993350903281e-05 300 Diff: 590.5089467763901 alpha value: 1.0254560482036439e-05 400 Diff: 279.2355946302414 alpha value: 1.0263893422517941e-05 500 Diff: 155.43169915676117 alpha value: 1.0270028681773919e-05 600 Diff: 96.61812579631805 alpha value: 1.0274280663010468e-05 700 Diff: 64.87719237804413 alpha value: 1.027728512597358e-05 800 Diff: 46.03102707862854 alpha value: 1.0279461929697766e-05 900 Diff: 34.00975978374481 alpha value: 1.0281092917213468e-05 Optimizer found with x = [-1.68825261 5.31853629 -3.45322318 ... 1.59365232 -2.85114689 5.04026352] and f(x)=-511573479.5792374 in 1000 iterationsTotal time taken: 1min 28s

下面是梯度下降法的情況，其中 alpha = 0.000001：

0 Diff: 26206321.312622845 alpha value: 1e-06 100 Diff: 112613.38076114655 alpha value: 1e-06 200 Diff: 21639.659786581993 alpha value: 1e-06 300 Diff: 7891.810685873032 alpha value: 1e-06 400 Diff: 3793.90934664011 alpha value: 1e-06 500 Diff: 2143.767760157585 alpha value: 1e-06 600 Diff: 1348.4947955012321 alpha value: 1e-06 700 Diff: 914.9099299907684 alpha value: 1e-06 800 Diff: 655.9336211681366 alpha value: 1e-06 900 Diff: 490.05882585048676 alpha value: 1e-06 Optimizer found with x = [-1.80862488 4.66644055 -3.08228401 ... 2.46891076 -2.57581774 5.34672724] and f(x)=-511336392.26658595 in 1000 iterationsTotal time taken: 1min 16s

我們可以發(fā)現(xiàn)，梯度下降法的速度比最速下降法略快（幾秒或幾分鐘）。但更重要的是，最速下降法采取的步長(zhǎng)比梯度下降法更加合理，盡管梯度下降法的α的值并非最優(yōu)。在上述示例中， 對(duì)于梯度下降算法，f(xprex)和f(curr)在第900次迭代時(shí)的差為450。而最速下降法在很多次迭代前就已經(jīng)達(dá)到這個(gè)值了（大約在第300次到第400次迭代之間）。

因此，我們嘗試限制最速下降法的迭代次數(shù)為300，輸出如下：

0 Diff: 118618752.30065191 alpha value: 8.569151292666038e-06 100 Diff: 8281.239207088947 alpha value: 1.1021416896567156e-05 200 Diff: 1463.1741587519646 alpha value: 1.1087402059869253e-05 300 Diff: 526.3014997839928 alpha value: 1.1106776689082503e-05 Optimizer found with x = [-1.33362899 5.89337889 -3.31827817 ... 1.77032789 -2.86779156 4.56444743] and f(x)=-511526291.3367646 in 400 iterationsTime taken: 35.8s

可以發(fā)現(xiàn)，最速下降法的速度實(shí)際更快。在此情形中，我們?cè)诿看蔚褂酶俚牟綌?shù)就能逼近最優(yōu)值。事實(shí)上，如果你的目標(biāo)是估計(jì)最優(yōu)值，最速下降法會(huì)比梯度下降法更合適。對(duì)于低維度的函數(shù)，10步的最速下降法就會(huì)比經(jīng)過1000次迭代的梯度下降法更接近最優(yōu)值。

下面這個(gè)例子中，我們使用了一個(gè)定義在?3?→?上的二次函數(shù)。10步后，最速下降法的得到函數(shù)值為 f(x) = -62434.18。而梯度下降法在1000步后得到的函數(shù)值為 f(x) = -61596.84。可以發(fā)現(xiàn)，最速下降法在10步后的結(jié)果就優(yōu)于梯度下降法在1000步后的結(jié)果。

需要記住的是，這種情形僅在處理二次函數(shù)的時(shí)候適用。整體而言，在每次迭代中都找到 αk的最優(yōu)值是較為困難的。對(duì)函數(shù) g(α) 求最優(yōu)值并不總能得到 αk 的最優(yōu)值。通常，我們會(huì)使用迭代的算法來對(duì)優(yōu)化函數(shù)求最小值。在這種情形下，最速下降法與梯度下降法相比就比較慢了。因此，最速下降法在實(shí)際應(yīng)用中并不常見。

總結(jié)

在本文中，我們學(xué)習(xí)了三種下降算法：

牛頓法（Newton's method）

牛頓法提供了對(duì)函數(shù)的二階近似，并在每一步都對(duì)函數(shù)進(jìn)行優(yōu)化。其最大的問題在于，在優(yōu)化過程中需要進(jìn)行矩陣轉(zhuǎn)換，對(duì)于多變量情形花銷過高（尤其是向量的特征較多的時(shí)候）。

梯度下降（Gradient Descent）

梯度下降是最常用的優(yōu)化算法。由于該算法在每步只對(duì)導(dǎo)數(shù)進(jìn)行計(jì)算，其花銷較低，速度更快。但是在使用該算法時(shí)，需要對(duì)步長(zhǎng)的超參數(shù)進(jìn)行多次的猜測(cè)和嘗試。

最速下降法（Steepest Descent）

最速下降法在每步都對(duì)函數(shù)的梯度向量尋找最優(yōu)步長(zhǎng)。它的問題在于，在每次迭代中需要對(duì)相關(guān)的函數(shù)進(jìn)行優(yōu)化，這會(huì)帶來很多花銷。對(duì)于二次函數(shù)的情形，盡管每步都涉及很多矩陣運(yùn)算，最速下降法的效果仍然更優(yōu)。