數字通信系統通常必須滿足規范和約束在時域(例如,建立時間)和頻域(例如,信噪比)中。作為一個額外的復雜功能,跨越連續時間和離散時間(采樣)信號邊界運行的系統設計人員必須應對混疊和成像問題。實際上,所有數字通信系統都屬于這一類,采樣數據約束可能對系統性能產生重大影響。在大多數數字通信系統中,連續時間到離散時間接口發生在數字 - 模擬(DAC)和模數(ADC)轉換過程中,這是數字和模擬域之間的接口。 。該接口的性質需要清楚的理解,因為與數字和模擬域之間的轉換相關聯的電平敏感偽像(例如,量化)經常與離散時間和連續時間之間的轉換的時間敏感問題(例如,混疊)混淆。 。這兩種現象是不同的,細微的區別在設計和調試系統中很重要。 (注意:所有數字信號必須固有地為離散時間,但模擬信號處理雖然通常是連續時間,但也可能處于離散時間 - 例如,使用開關電容電路。)
奈奎斯特定理表達了試圖用離散樣本表示連續時間信號的基本限制。基本上,具有每秒Fs采樣的采樣率的數據可以有效地表示帶寬高達Fs / 2Hz的信號。具有更大帶寬的采樣信號產生混疊:頻率大于Fs / 2的信號內容被折疊或混疊,返回到Fs / 2頻帶。這可能會產生嚴重的問題:一旦數據被采樣,就無法確定哪些信號分量來自所需頻段,哪些是別名。大多數數字通信系統處理帶限信號,要么是因為基本信道帶寬(如在ADSL雙絞線調制解調器中),要么是監管限制(如無線電廣播和蜂窩電話)。在許多情況下,信號帶寬被非常仔細地定義為應用標準的一部分;例如,用于蜂窩電話的GSM標準定義了大約200kHz的信號帶寬,IS-95蜂窩電話使用1.25MHz的帶寬,而DMT-ADSL雙絞線調制解調器利用1.1MHz的帶寬。在每種情況下,奈奎斯特準則可用于建立最小可接受的數據速率,以明確地表示這些信號:分別為400 kHz,2.5 MHz和2.2 MHz。必須小心使用濾波,以消除此所需帶寬之外的信號內容。 ADC之前的模擬濾波器通常稱為抗混疊濾波器,因為其功能是在A / D轉換器的采樣操作之前衰減超過奈奎斯特帶寬的信號。等效濾波功能遵循D / A轉換器,通常稱為平滑濾波器或重建濾波器。這種連續時間模擬濾波器可以衰減D / A轉換器輸出端出現的不需要的頻率圖像。
乍一看,抗混疊濾波器的要求相當簡單:通帶必須是當然準確地傳遞所需的輸入信號。阻帶必須充分衰減通帶外的任何干擾,使其殘留(濾波器之后的殘余)在A / D轉換器采樣后混疊到通帶中時不會損害系統性能。抗混疊濾波器的實際設計可能非常具有挑戰性。如果帶外干擾信號非常強并且非常接近所需信號的通過頻率,則對濾波器阻帶和過渡帶窄度的要求可能非常嚴格。嚴格的濾波器要求需要使用具有積極濾波器滾降功能的拓撲結構的高階濾波器。遺憾的是,具有這種特性的濾波器的拓撲結構(例如,Chebychev)通常對元件匹配提出了昂貴的要求,并且傾向于在通帶的邊緣引入相位失真,從而危及信號恢復。設計人員還必須了解抗混疊濾波器的失真要求:通常,模擬抗混疊濾波器的通帶失真應至少與A / D轉換器一樣好(因為任何帶外諧波)介紹將有別名)。即使不存在強干擾源,也必須在抗混疊濾波器設計中考慮噪聲。帶外噪聲混疊回基帶,就像帶外干擾一樣。例如,如果轉換器之前的濾波器帶寬為奈奎斯特頻帶的兩倍,則信噪比(SNR)將降低3 dB(假設為白噪聲),而4倍奈奎斯特的帶寬將導致降級6分貝。當然,如果SNR綽綽有余,寬帶噪聲可能不是主要的約束條件。
別名具有頻率轉換方面,可以通過欠采樣技術利用它。要理解欠采樣,必須仔細考慮奈奎斯特約束的定義。請注意,對帶寬, F s / 2的信號進行采樣,要求最小采樣率大于F s 。這個F s / 2帶寬理論上可以位于頻譜中的任何位置[例如, NF s 到( N +1/2)F s ],而不僅僅是從dc到 F s / 2。像混頻器一樣,混疊動作可用于將RF或IF頻率向下轉換到基帶。基本上,帶中的信號 NF s F s N-1/2)F s
欠采樣為A / D轉換器設計人員提出了更多挑戰:高速輸入信號不僅需要更寬的輸入帶寬,而且需要更高的輸入帶寬。 D轉換器的采樣保持(SHA)電路;它們還對A / D轉換器的抖動性能及其采樣時鐘提出了更嚴格的要求。為了說明,比較采樣100-kHz正弦波信號的基帶系統和采樣100-MHz正弦波信號的IF欠采樣系統。在基帶系統中,100 ps的抖動誤差產生最大信號誤差為滿量程的0.003%(峰 - 峰值) - 可能無關緊要。在IF欠采樣情況下,相同的100 ps誤差會產生最大信號誤差為滿量程的3%。

過采樣與欠采樣并不完全相反(實際上,系統可能同時進行過采樣和欠采樣)。過采樣包括以大于奈奎斯特準則建議的速率對所需信號進行采樣:例如,以1.6 MHz采樣200 kHz信號,而不是所需的最小400 kHz。過采樣率定義為:OSR =采樣率/(2×輸入帶寬)
過采樣具有幾個吸引人的優勢(圖2)。較高的采樣率可以顯著簡化抗混疊濾波器的過渡帶要求。在上面的示例中,對400 kHz的200 kHz帶寬信號進行采樣需要“完美”的墻壁抗混疊濾波器,因為201 kHz的干擾信號將在帶內混疊到199 kHz。 (由于“完美”濾波器是不可能的,大多數系統采用一定程度的過采樣,或者依靠系統規范來提供頻率保護頻帶,這可以排除緊鄰頻率的干擾。)另一方面,1.6 MHz的采樣移動第一個關鍵別名頻率輸出到1.4 MHz,允許抗混疊濾波器的過渡頻帶高達1.2 MHz。
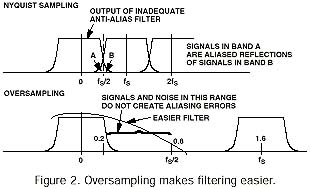
當然,如果頻率接近200 kHz的干擾信號非常強大根據所需信號,轉換器需要額外的動態范圍,以便能夠捕獲兩個信號而不會產生限幅(參見第IV部分,模擬對話 31-2,討論動態范圍問題。)轉換后,過采樣數據可以直接傳遞給數字解調器,或者抽取到接近奈奎斯特的數據速率。抽取涉及通過類似于模擬抗混疊濾波器的數字濾波操作來降低數字采樣率。精心設計的數字抽取濾波器提供了減少A / D轉換的量化噪聲的額外優勢。對于傳統的A / D轉換器,對于每個倍頻程(因子2)抽取,實現了對應于量化噪聲降低3dB的轉換增益。如上所述,使用1.6 MHz采樣率進行過采樣,并將閾值降至400 kHz的奈奎斯特速率,我們可以實現高達6 dB的SNR增益(兩個八度)。
噪聲整形轉換器,例如sigma-delta調制器,是過采樣轉換器的一種特殊情況。調制器的采樣率是其高速時鐘速率,抗混疊濾波器可以非常簡單。 Sigma delta調制器使用反饋電路來對量化噪聲的頻率內容進行整形,將其推向遠離感興趣的信號頻帶的頻率,在那里可以將其濾除。這僅在過采樣系統中是可能的,因為根據定義,過采樣系統提供超出感興趣的信號頻帶的頻率空間。傳統轉換器通過抽取允許3 dB /倍頻程轉換增益,Σ-Δ轉換器可提供9,15,21或更多dB /倍頻程增益,具體取決于調制器設計的性質(高階環路)或者級聯架構,提供更積極的性能增益。
在傳統的轉換器中,量化噪聲通常近似為“白色” - 在頻譜上均勻分布。對于N比特轉換器,在0到Fs / 2的帶寬范圍內,滿量程信號 - 量化噪聲比(SQNR)將為(6.02 N + 1.76)dB。對于大多數情況,“白色”噪聲近似效果相當好,但是當時鐘和單音模擬頻率通過簡單的整數比相關時會出現問題 - 例如,當模擬輸入恰好是時鐘頻率的1/4時。在這種情況下,量化噪聲傾向于“聚集”到馬刺中,這與白噪聲有相當大的不同。
雖然近年來有很多關于A / D轉換器的抗混疊和欠采樣操作的文章,但D / A轉換器輸出端的相應濾波器問題卻遠遠不夠。在D / A轉換器的情況下,不是令人擔憂的不可預測的干擾源,而是DAC輸出信號的非常可預測的頻率圖像。為了更好地理解DAC圖像現象,圖3(a,b)說明了時域和頻域的理想正弦波和DAC輸出。重要的是要意識到這些頻率圖像不是幅度量化的結果:它們甚至存在于“完美”的高分辨率DAC中。圖像的原因是D / A轉換器輸出在每個時鐘周期內僅與一次完全匹配所需信號。在剩余的時鐘周期內,DAC輸出和理想信號不同,從而產生誤差能量。該時域誤差的相應頻率圖表顯示為一組傅里葉級數圖像頻率(c)。對于以F 時鐘 更新的DAC合成的頻率為F out 的輸出信號,圖像出現在 NF clock ± F out 。根據
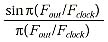
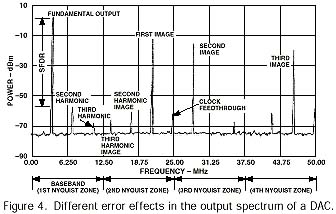
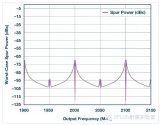
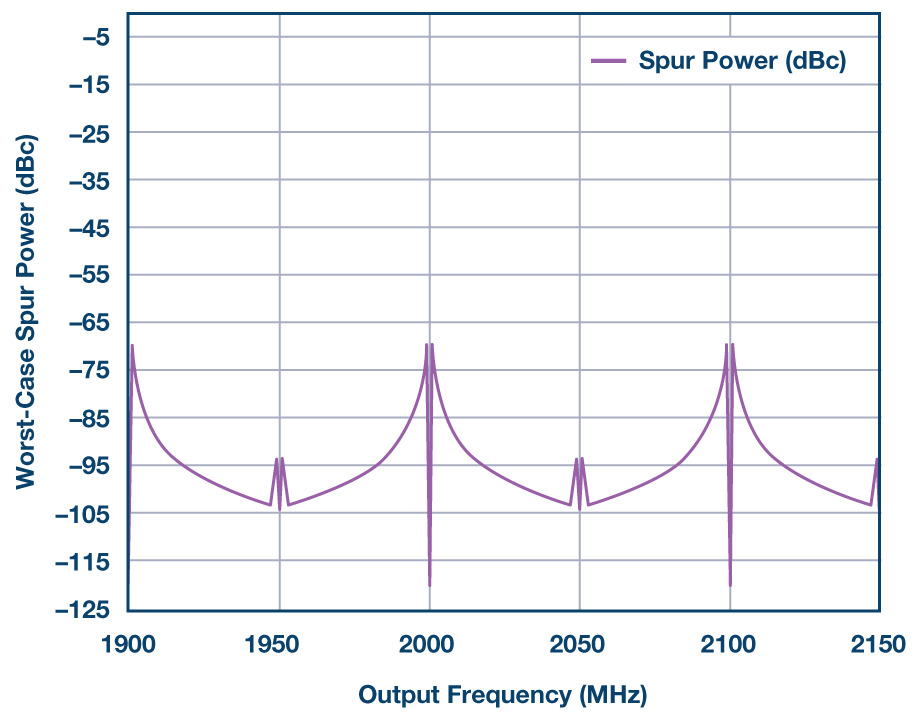
這些圖像的幅度隨著頻率的增加而下降,在時鐘頻率的整數倍周圍留下非常弱的圖像能量的“零點”。大多數DAC輸出都具有一定程度的時鐘饋通,可以在時鐘的倍數處表現為頻譜能量。這會產生如圖4所示的頻譜。
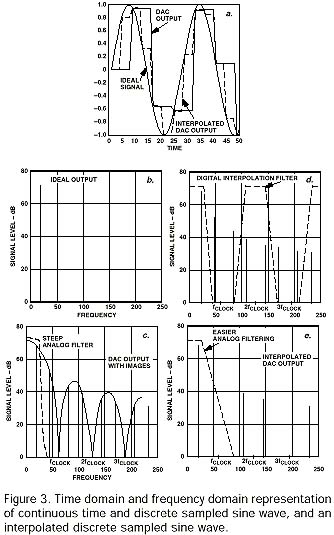
DAC重建濾波器的任務是傳遞所需的最高輸出頻率Foutmax,并阻止位于F 時鐘的最低圖像頻率 - F outmax ,表示平滑濾波器過渡帶F clock -2F outmax 。
這表明當一個人試圖合成接近奈奎斯特極限的信號時(F outmax = F < sub> clock / 2),濾波器轉換變得非常陡峭。為了保持濾波器問題易于處理,許多設計人員使用經驗法則,DAC時鐘應至少是最大所需輸出頻率的三倍。除了濾波器困難之外,高頻輸出可能會被sinx / x包絡明顯衰減:F 時鐘 / 3處的信號衰減1.65 dB,一個信號在F 時鐘 / 2衰減3.92 dB。
過采樣可以改善D / A濾波器問題,就像它在ADC情況下有所幫助一樣。 (事實上,更重要的是,因為人們不必擔心強干擾問題。)D / A需要插值濾波器。數字插值濾波器通過生成所需信號的中間數字樣本來增加D / A的有效數據速率,如圖3(a)所示。頻域結果顯示在(d,e)中:在這種情況下,2×插值抑制了DAC輸出的前兩個圖像,從F clock -2F outmax 到2F clock -2F outmax 的。這允許簡化濾波器并且可以允許更保守的極點放置 - 以減少通帶相位失真問題,這是模擬濾波器的頻繁副作用。數字插值濾波器可以用可編程DSP和ASIC實現,甚至可以通過與D / A轉換器(例如,AD9761,AD9774)的集成來實現。與模擬濾波器一樣,插值濾波器的關鍵性能考慮因素是通帶平坦度,阻帶抑制(抑制圖像多少?)和過渡帶的窄度(理論奈奎斯特帶寬的多少(F <通帶中允許sub> clock / 2)?
DAC可用于欠采樣應用,但功效低于ADC。可以使用帶通重建濾波器來選擇其中一個圖像(而不是基本圖像),而不是使用低通重建濾波器來拒絕不需要的圖像。這類似于ADC欠采樣,但有一些復雜性。如圖3所示,圖像幅度實際上是頻域中sinx / x包絡上的點。 sinx / x隨頻率的減小幅度表明較高頻率的圖像將被衰減,并且衰減量可以根據輸出頻率相對于時鐘頻率的倍數位于何處而變化很大。 sinx / x包絡是DAC“零階保持”效應的結果(DAC輸出在大部分時鐘周期內保持固定在目標輸出)。這對于基帶DAC是有利的,但對于欠采樣應用,輸出理想脈沖的“歸零”DAC不會受到較高頻率衰減的影響。由于理想的脈沖在物理上是不切實際的,因此實際的歸零DAC將會有一些頻域包絡。這種效應可以通過數字濾波進行預補償,但在較高輸出頻率下DAC動態性能的下降通常會限制DAC欠采樣方法的吸引力。
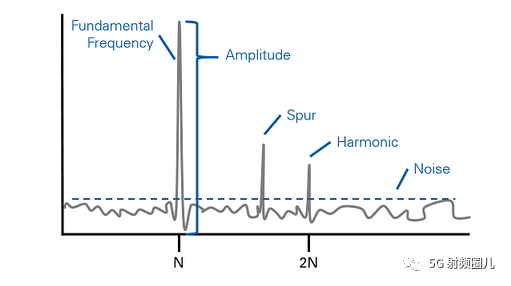
頻域圖像只是DAC輸出頻譜中眾多雜散能量源之一。雖然上面討論的圖像即使在D / A轉換器本身“完美”時也存在,但是大多數其他雜散能量源是D / A轉換器非理想性的結果。在通信應用中,發射機信號處理必須確保這些雜散輸出低于規定的電平,以確保它們不會對通信介質中的其他信號產生干擾。有幾種規格可用于測量頻域中D / A轉換器的動態性能(見圖4):
無雜散動態范圍(SFDR) - 所需信號(可能是單音或多音)與被測頻段中最高雜散信號之間的信號強度(dB)差異(圖4)。通常,最強的寄生響應是所需輸出信號的諧波之一。在某些應用中,SFDR可以在非常窄的范圍內指定,不包括任何諧波。對于窄帶發射器,DAC處理類似于單個強音的信號,SFDR通常是感興趣的主要規格。
總諧波失真(THD) - 雖然SFDR表示測量頻帶中最高單個雜散的強度,但THD增加了所有諧波雜散的能量(例如,前8個)。
雙音互調失真(IMD) - 如果D / A轉換器具有非線性,它將在合成信號之間產生混合動作。例如,如果非線性DAC試圖合成1.1和1.2 MHz的信號,則將以100 kHz(差頻)和2.3 MHz(和頻)生成二階互調產物。三階互調產物將在1.3 MHz(2×1.2 - 1.1)和1.0 MHz(2×1.1 - 1.2)下生成。該應用程序確定哪些互調產品存在最大問題,但三階產品通常更麻煩,因為它們的頻率往往非常接近原始信號的頻率。
信號到-noise-plus-distortion (SINAD)-THD僅測量不需要的諧波能量。 SINAD測量指定部分頻譜中的所有非信號能量,包括熱噪聲,量化噪聲,諧波雜散和非諧波相關的雜散信號。例如,CDMA(碼分多址)系統涉及指定帶寬中的總噪聲能量:SINAD是這些應用的更準確的品質因數。 SINAD可能是最難測量的,因為許多頻譜分析儀沒有足夠低的輸入噪聲。測量DAC SINAD的最簡單方法是使用具有顯著優越性能的ADC。
這些規范或其他來自它們的規范代表DAC在信號合成應用中的主要性能指標。除此之外,還有許多傳統的DAC規范,其中許多與視頻DAC或其他應用有關,在DAC數據表中仍然很普遍。這些包括積分非線性(INL),微分非線性(DNL),毛刺能量(更準確地說,毛刺脈沖),建立時間,差分增益和微分相位。雖然這些時域規范與真正的動態測量值之間可能存在一定的相關性,但時域規范在預測動態性能方面并不擅長。
即使在查看動態特性(例如SFDR和SINAD)時,記住要合成的信號的特定性質也非常重要。像QPSK這樣的簡單調制方法傾向于產生強窄帶信號。 DAC的SFDR性能在滿量程附近重現單音可能是該部件適用于該應用的良好指標。另一方面,現代系統通常具有具有許多不同特性的信號,例如同時合成的多個音調(用于寬帶無線電或離散多音調(DMT)調制方案)和直接序列擴頻調制(例如CDMA)。這些更復雜的信號往往會在DAC的中低規模轉換附近花費更多時間,對于D / A轉換器性能的不同方面比合成強單音正弦波的系統敏感。由于仿真模型還不夠精確,無法正確捕捉這些差異的微妙之處,因此最安全的方法是在極端模擬最終應用的條件下表征DAC。在各種條件下表征的這些要求說明了D / A轉換器數據表的大小和豐富程度的增長。
-
轉換器
+關注
關注
27文章
8741瀏覽量
147690 -
dac
+關注
關注
43文章
2308瀏覽量
191342 -
數字通信
+關注
關注
1文章
146瀏覽量
22525
發布評論請先 登錄
相關推薦




 數字通信系統中雜散信號的產生原因
數字通信系統中雜散信號的產生原因











評論