動力學主要研究作用于物體的力與物體運動的關系。
車輛動力學模型一般用于分析車輛的平順性和車輛操縱的穩定性。
對于車來說,研究車輛動力學,主要是研究車輛輪胎及其相關部件的受力情況。
比如縱向速度控制,通過控制輪胎轉速實現;
橫向航向控制,通過控制輪胎轉角實現。
正常情況下,車輛上的作用力沿著三個不同的軸分布:
縱軸上的力包括驅動力和制動力,以及滾動阻力和拖拽阻力作滾擺運動;
橫軸上的力包括轉向力、離心力和側風力,汽車繞橫軸作俯仰運動;
立軸上的力包括車輛上下振蕩施加的力,汽車繞立軸作偏擺或轉向運動。
無論是LQR或是MPC控制,都需要有車輛的模型作為基礎。
本文由社區開發者——卜大鵬撰寫,整理出Apollo控制算法中使用的車輛動力學模型的推導過程。
車輛動力學模型
以下,ENJOY
首先,根據牛頓第二定律結合車輛前后輪受力,有:

根據力矩平衡結合車輛前后輪受力和受力點到車輛重心距離,有:

上述兩式中,汽車質量m、轉動慣量Iz、前軸到重心距離lf和后軸到重心距離lr都是可測量的。
為了求解兩等式,需要分別求得車輛橫向加速度ay和前輪橫向受力Fyf和后輪橫向受力Fyr。
橫向加速度可以分解為由橫向位移產生的加速度和向心加速度。

y為橫向位移,psi為航向角,Vx為縱向速度。這樣橫向加速度就分解為位移和航向角的表達式。
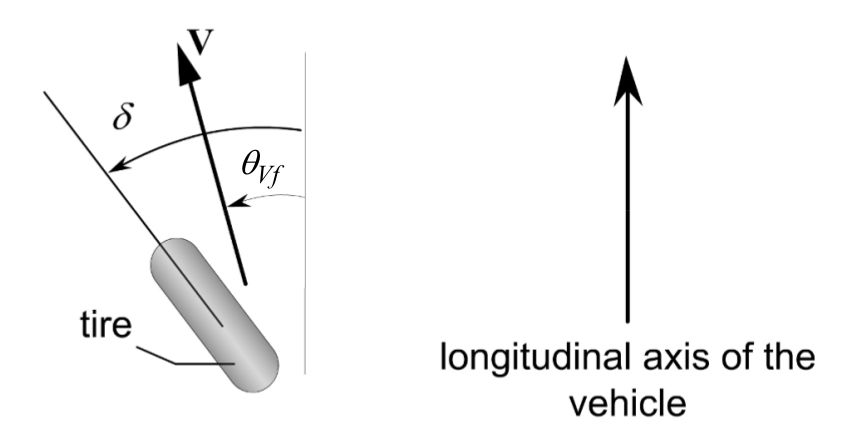
前輪橫向受力可以近似為公式4,其中Caf為前輪側偏剛度,delta為前輪轉角,theta_vf為前輪側偏角。

后輪橫向受力可以近似為公式5,其中Car為后輪側偏剛度,theta_vr為后輪側偏角。

公式4和公式5可以理解為實測數據標定后得到近似公式。
在簡化環境因素下,側偏剛度可以由簡化的輪胎模型求出,前輪轉角為可獲取量,只需想辦法表示出前后輪的側偏角。
至此,上文提到的各變量在車體上的示意圖如下:
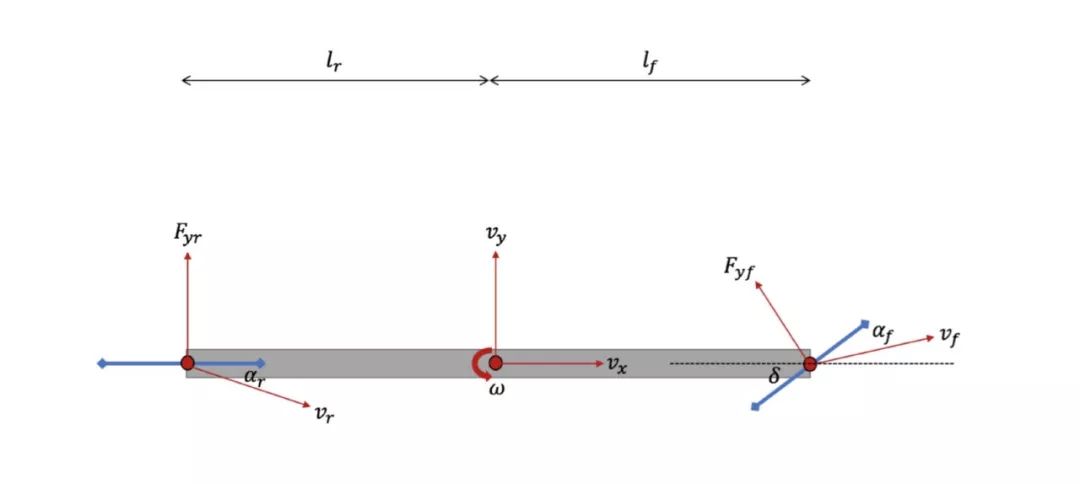
根據上圖可知,tan(theta)等于車輛橫向速度比縱向速度,而橫向速度由車輛自身橫向速度和繞重心轉動速度組成。
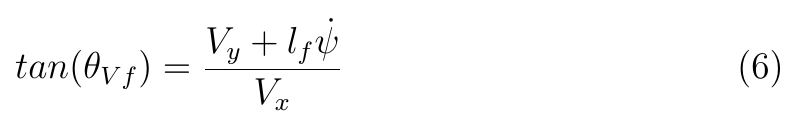
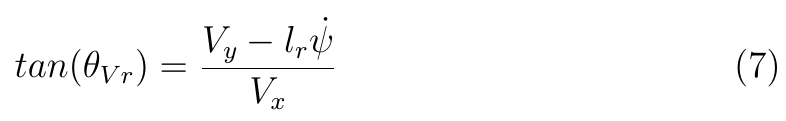
在小角度轉向假設下,有:


至此,把變化后的各變量表達式代入公式1和公式2,有:
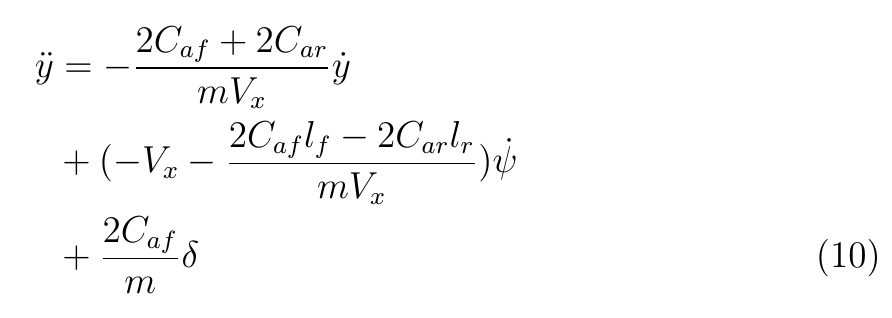
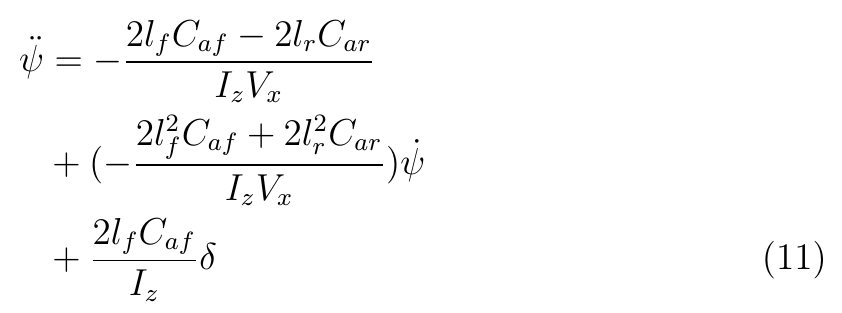
設e1為橫向偏差,e2為航向角偏差,可以得到如下關系。
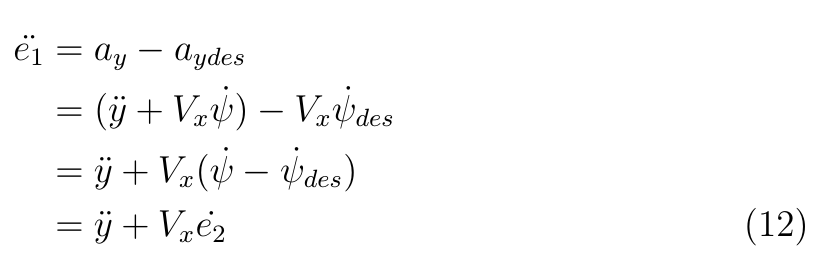
在勻速假設下,上式可進一步推導出:

帶入公式10和公式11可以得到兩個偏差的表達式:
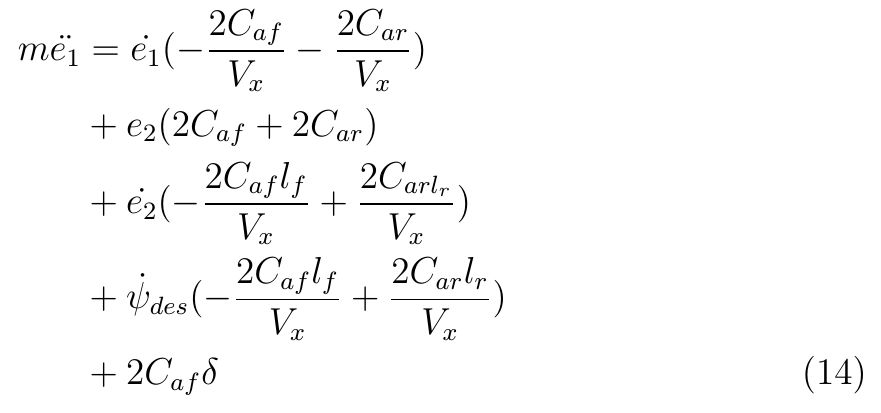
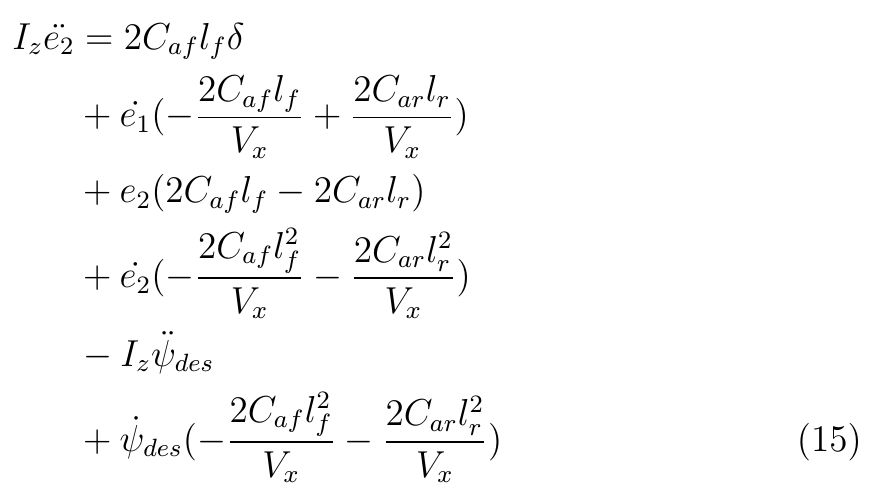
轉換為狀態空間的表達式:
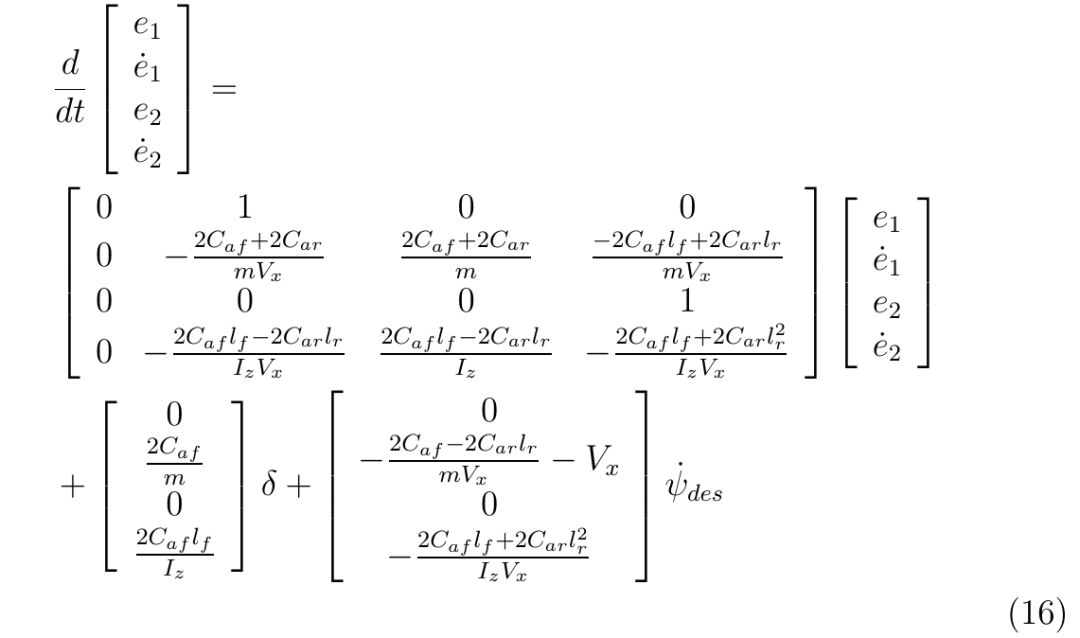
這樣就得到了在
小角度側偏角
勻速
不考慮環境因素
假設下,車輛的動力學模型表達式。
令:
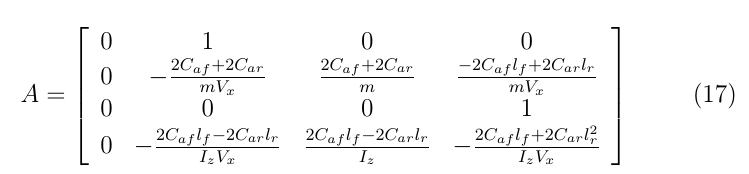

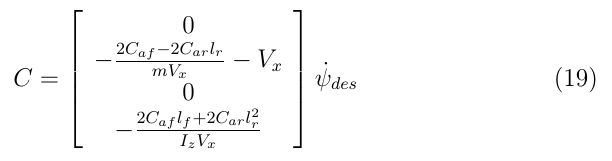


得到狀態方程:

式中,前輪側偏剛度Caf、后輪側偏剛度Car、車身質量m、轉動慣量Iz、前輪到重心距離lf、后輪到重心距離lr都是常量;
每個時刻的橫向偏差e1、航向偏差e2、縱向速度Vx、前輪轉角delta都是可測量量;
目標航向psi是可獲取量。
這樣每個運算周期通過傳感器測得的數值更新測量量就可以用這個模型通過相應算法實現目標軌跡的跟蹤了。
但因為需要使用計算機進行數值計算,推導截至到上面的連續模型還不夠,還需要對上述模型進行離散化。
對于連續系統有:
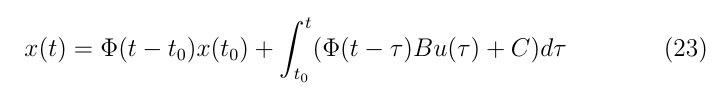
令采樣周期為T,t0=kT,t=(k+1)T,即考慮k到k+1時刻的狀態響應,有:
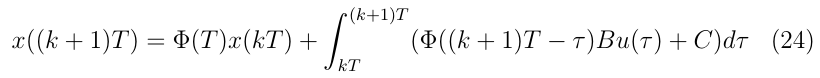
考慮在采樣周期內u不變,C為常數,有
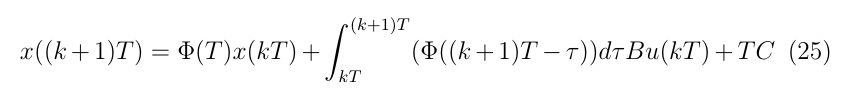
對上式積分中做變量替換,令t=(k+1)T-tau,有
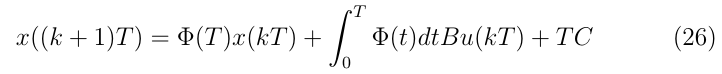
將上式與定常離散線性系統的狀態方程
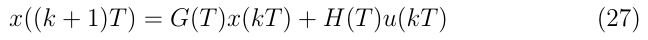
比較可知,要使兩式對任意x(kT)和u(kT)成立,有

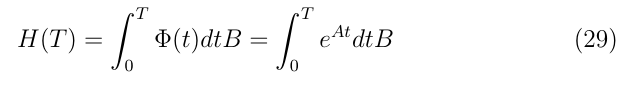
公式23到公式29即為連續狀態空間到離散狀態空間的精確離散化推導過程。為了便于后續計算,還需要對精確離散化進一步進行近似離散化,因為有

對上式分子分母同時做泰勒展開,取前兩項,有
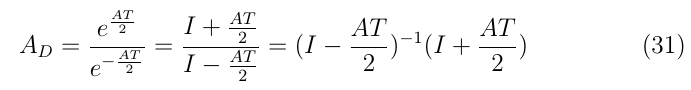
同樣,對式23進行泰勒展開,取前一項,有
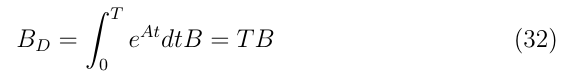
剩下的常數項,顯然有

至此,得到了連續模型轉換為后續算法可用的近似離散化模型
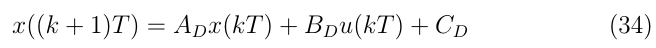
-
控制算法
+關注
關注
4文章
166瀏覽量
21757 -
動力學
+關注
關注
0文章
106瀏覽量
17000 -
Apollo
+關注
關注
5文章
342瀏覽量
18493
原文標題:開發者說 | Apollo控制算法之汽車動力學模型
文章出處:【微信號:Apollo_Developers,微信公眾號:Apollo開發者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于多體系統動力學的空氣懸架大客車平順性試驗仿真研究
帶齒輪傳動的機車-軌道空間耦合動力學模型
飛行器動力學參數在線辨識EKF算法實驗流程
熱分析動力學
車輛動力學控制系統(VDC)是什么意思
如何使用DSPACE實現嵌入式車輛動力學仿真平臺的開發設計
經緯恒潤自主研發的綜合車輛動力學仿真軟件ModelBase
綜合車輛動力學仿真軟件ModelBase的簡單介紹
鋼軌打磨對車輛系統動力學的影響
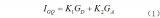




 Apollo控制算法中使用的車輛動力學模型的推導過程
Apollo控制算法中使用的車輛動力學模型的推導過程











評論