極大似然估計(jì)(Maximum likelihood estimation, 簡(jiǎn)稱(chēng)MLE)是很常用的參數(shù)估計(jì)方法,極大似然原理的直觀想法是,一個(gè)隨機(jī)試驗(yàn)如有若干個(gè)可能的結(jié)果A,B,C,... ,若在一次試驗(yàn)中,結(jié)果A出現(xiàn)了,那么可以認(rèn)為實(shí)驗(yàn)條件對(duì)A的出現(xiàn)有利,也即出現(xiàn)的概率P(A)較大。也就是說(shuō),如果已知某個(gè)隨機(jī)樣本滿(mǎn)足某種概率分布,但是其中具體的參數(shù)不清楚,參數(shù)估計(jì)就是通過(guò)若干次試驗(yàn),觀察其結(jié)果,利用結(jié)果推出參數(shù)的大概值。極大似然估計(jì)是建立在這樣的思想上:已知某個(gè)參數(shù)能使這個(gè)樣本出現(xiàn)的概率最大,我們當(dāng)然不會(huì)再去選擇其他小概率的樣本,所以干脆就把這個(gè)參數(shù)作為估計(jì)的真實(shí)值(請(qǐng)參見(jiàn)“百度百科”)。
本文以一個(gè)簡(jiǎn)單的離散型分布的例子,模擬投擲硬幣估計(jì)頭像(head)向上的概率。投擲硬幣落到地面后,不是head向上就是tail朝上,這是一個(gè)典型的伯努利實(shí)驗(yàn),形成一個(gè)伯努利分布,有著如下的離散概率分布函數(shù):
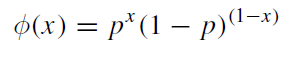
其中,x等于1或者0,即結(jié)果,這里用1表示head、0表示tail。
對(duì)于n次獨(dú)立的投擲,很容易寫(xiě)出其似然函數(shù):
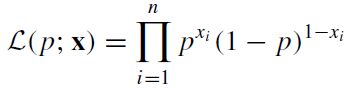
現(xiàn)在想用極大似然估計(jì)的方法把p估計(jì)出來(lái)。就是使得上面這個(gè)似然函數(shù)取極大值的情況下的p的取值,就是要估計(jì)的參數(shù)。
首先用Python把投擲硬幣模擬出來(lái):
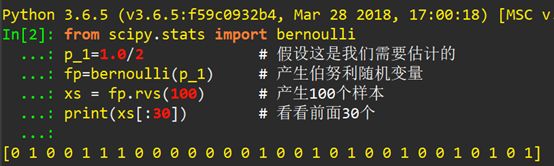
通過(guò)此模擬,使用sympy庫(kù)把似然函數(shù)寫(xiě)出來(lái):

從上面的結(jié)論可以看出,作100次伯努利實(shí)驗(yàn),出現(xiàn)positive、1及head的數(shù)目是53個(gè),相應(yīng)的0也就是tail的數(shù)目是47個(gè),比較接近我們?cè)O(shè)的初始值0.5即1.0/2(注意:現(xiàn)在我們假設(shè)p是未知的,要去估計(jì)它,看它經(jīng)過(guò)Python的極大似然估計(jì)是不是0.5!)。
下面,我們使用Python求解這個(gè)似然函數(shù)取極大值時(shí)的p值:
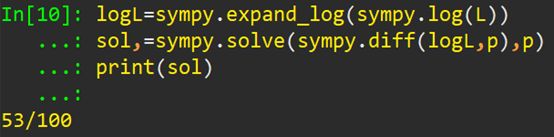
結(jié)果沒(méi)有什么懸念,53/100的值很接近0.5!
取對(duì)數(shù)后,上面Python的算法最后實(shí)際上是求解下式為0的p值:
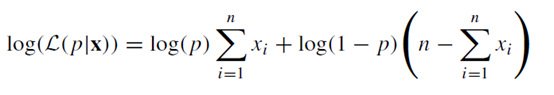
上式留給網(wǎng)友自行推導(dǎo),很多資料都可找到該式。這個(gè)式子,是著名的Logistic回歸參數(shù)估計(jì)的極大似然估計(jì)算法的基礎(chǔ)。
進(jìn)一步,為了更加直觀的理解投擲硬幣的伯努利實(shí)驗(yàn),我們給出以均值(均值為100*0.5=50)為中心對(duì)稱(chēng)的加總離散概率(概率質(zhì)量函數(shù)(probability mass function),Python里面使用pmf函數(shù)計(jì)算):
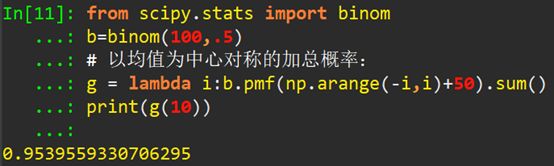
對(duì)于上面的Python代碼,可以通過(guò)下圖更好地去理解:
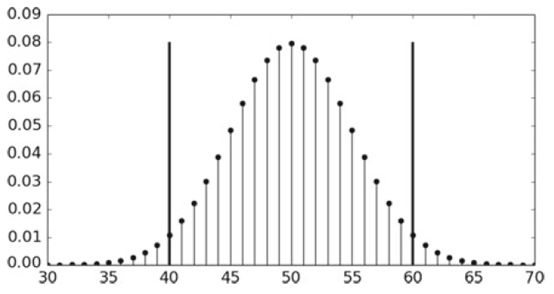
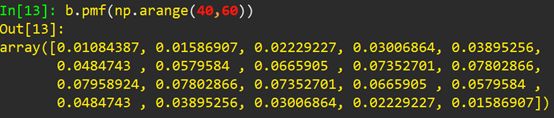
把這20個(gè)離散的概率全部顯示出來(lái),也可以看到在0.08左右取到它們的最大值:
本文針對(duì)簡(jiǎn)單的離散概率質(zhì)量函數(shù)的分布使用Python進(jìn)行了極大似然估計(jì),同時(shí)該方法可以應(yīng)用于連續(xù)分布的情形,只要通過(guò)其概率密度函數(shù)得出其似然函數(shù)即可。希望網(wǎng)友把本文的代碼實(shí)踐一遍,也可以和R語(yǔ)言、SAS等軟件得到的結(jié)論相比較,從而得到更好的極大似然估計(jì)的實(shí)現(xiàn)方法。
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4345瀏覽量
62874 -
python
+關(guān)注
關(guān)注
56文章
4807瀏覽量
84950 -
最大似然估計(jì)
+關(guān)注
關(guān)注
0文章
2瀏覽量
1661
原文標(biāo)題:用Python實(shí)現(xiàn)極大似然估計(jì)
文章出處:【微信號(hào):magedu-Linux,微信公眾號(hào):馬哥Linux運(yùn)維】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦



這6點(diǎn)幫你解決參數(shù)未知的重要問(wèn)題 | AI知識(shí)科普
巴斯卡分布中未知參數(shù)的估計(jì)
多傳感器的極大似然配準(zhǔn)算法研究
基于極大似然法的椒鹽噪聲濾波算法
基于平均似然比的魯棒性突發(fā)檢測(cè)
基于正交訓(xùn)練序列的MIMO系統(tǒng)聯(lián)合最大似然時(shí)頻同步和信道估計(jì)
最大似然檢測(cè)算法認(rèn)識(shí)與理解
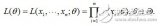
基于極大似然的非監(jiān)督噪聲功率譜估計(jì)方法





 如何用Python實(shí)現(xiàn)極大似然估計(jì)?
如何用Python實(shí)現(xiàn)極大似然估計(jì)?










評(píng)論