最大似然檢測算法認識與理解
最大似然檢測
最大似然檢測(Maximum Likelihood,ML)檢測,也被稱作最大似然序列估計(MLSE),從嚴格意義上講它不是均衡方案而是接收機方式,其中接收端的檢測處理顯式地考慮了無線信道時間彌散的影響。從根本上講,ML檢測器考慮了時間彌散對接收信號的影響,用整個接收信號來確定最有可能被發送的序列。為了實現最大似然檢測,通常使用Viterbi算法。然而,盡管基于Viterbi算法的最大似然檢測被廣泛應用于諸如GSM的2G通信,該算法還是因為太過復雜而無法應用在LTE上,這是因為更寬的傳輸帶寬將導致更廣泛的信道頻率選擇性和更高的采樣速率。
總的來說,信號信息經過信道估計和均衡后,通過資源逆映射映射到不同的物理信道上進行處理
一、最大似然
假設我們需要調查我們學校的男生和女生的身高分布。你怎么做啊?你說那么多人不可能一個一個去問吧,肯定是抽樣了。假設你在校園里隨便地活捉了100個男生和100個女生。他們共200個人(也就是200個身高的樣本數據,為了方便表示,下面,我說“人”的意思就是對應的身高)都在教室里面了。那下一步怎么辦啊?你開始喊:“男的左邊,女的右邊,其他的站中間!”。然后你就先統計抽樣得到的100個男生的身高。假設他們的身高是服從高斯分布的。但是這個分布的均值u和方差?2我們不知道,這兩個參數就是我們要估計的。記作θ=[u, ?]T。
用數學的語言來說就是:在學校那么多男生(身高)中,我們獨立地按照概率密度p(x|θ)抽取100了個(身高),組成樣本集X,我們想通過樣本集X來估計出未知參數θ。這里概率密度p(x|θ)我們知道了是高斯分布N(u,?)的形式,其中的未知參數是θ=[u, ?]T。抽到的樣本集是X={x1,x2,…,xN},其中xi表示抽到的第i個人的身高,這里N就是100,表示抽到的樣本個數。
由于每個樣本都是獨立地從p(x|θ)中抽取的,換句話說這100個男生中的任何一個,都是我隨便捉的,從我的角度來看這些男生之間是沒有關系的。那么,我從學校那么多男生中為什么就恰好抽到了這100個人呢?抽到這100個人的概率是多少呢?因為這些男生(的身高)是服從同一個高斯分布p(x|θ)的。那么我抽到男生A(的身高)的概率是p(xA|θ),抽到男生B的概率是p(xB|θ),那因為他們是獨立的,所以很明顯,我同時抽到男生A和男生B的概率是p(xA|θ)* p(xB|θ),同理,我同時抽到這100個男生的概率就是他們各自概率的乘積了。用數學家的口吻說就是從分布是p(x|θ)的總體樣本中抽取到這100個樣本的概率,也就是樣本集X中各個樣本的聯合概率,用下式表示:
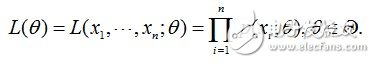
這個概率反映了,在概率密度函數的參數是θ時,得到X這組樣本的概率。因為這里X是已知的,也就是說我抽取到的這100個人的身高可以測出來,也就是已知的了。而θ是未知了,則上面這個公式只有θ是未知數,所以它是θ的函數。這個函數放映的是在不同的參數θ取值下,取得當前這個樣本集的可能性,因此稱為參數θ相對于樣本集X的似然函數(likehood function)。記為L(θ)。
這里出現了一個概念,似然函數。還記得我們的目標嗎?我們需要在已經抽到這一組樣本X的條件下,估計參數θ的值。怎么估計呢?似然函數有啥用呢?那咱們先來了解下似然的概念。
直接舉個例子:
某位同學與一位獵人一起外出打獵,一只野兔從前方竄過。只聽一聲槍響,野兔應聲到下,如果要你推測,這一發命中的子彈是誰打的?你就會想,只發一槍便打中,由于獵人命中的概率一般大于這位同學命中的概率,看來這一槍是獵人射中的。
這個例子所作的推斷就體現了極大似然法的基本思想。
再例如:下課了,一群男女同學分別去廁所了。然后,你閑著無聊,想知道課間是男生上廁所的人多還是女生上廁所的人比較多,然后你就跑去蹲在男廁和女廁的門口。蹲了五分鐘,突然一個美女走出來,你狂喜,跑過來告訴我,課間女生上廁所的人比較多,你要不相信你可以進去數數。呵呵,我才沒那么蠢跑進去數呢,到時還不得上頭條。我問你是怎么知道的。你說:“5分鐘了,出來的是女生,女生啊,那么女生出來的概率肯定是最大的了,或者說比男生要大,那么女廁所的人肯定比男廁所的人多”。看到了沒,你已經運用最大似然估計了。你通過觀察到女生先出來,那么什么情況下,女生會先出來呢?肯定是女生出來的概率最大的時候了,那什么時候女生出來的概率最大啊,那肯定是女廁所比男廁所多人的時候了,這個就是你估計到的參數了。
從上面這兩個例子,你得到了什么結論?
回到男生身高那個例子。在學校那么男生中,我一抽就抽到這100個男生(表示身高),而不是其他人,那是不是表示在整個學校中,這100個人(的身高)出現的概率最大啊。那么這個概率怎么表示?哦,就是上面那個似然函數L(θ)。所以,我們就只需要找到一個參數θ,其對應的似然函數L(θ)最大,也就是說抽到這100個男生(的身高)概率最大。這個叫做θ的最大似然估計量,記為:
![]()
有時,可以看到L(θ)是連乘的,所以為了便于分析,還可以定義對數似然函數,將其變成連加的:
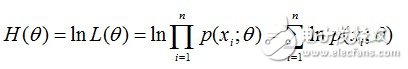
好了,現在我們知道了,要求θ,只需要使θ的似然函數L(θ)極大化,然后極大值對應的θ就是我們的估計。這里就回到了求最值的問題了。怎么求一個函數的最值?當然是求導,然后讓導數為0,那么解這個方程得到的θ就是了(當然,前提是函數L(θ)連續可微)。那如果θ是包含多個參數的向量那怎么處理啊?當然是求L(θ)對所有參數的偏導數,也就是梯度了,那么n個未知的參數,就有n個方程,方程組的解就是似然函數的極值點了,當然就得到這n個參數了。
最大似然估計你可以把它看作是一個反推。多數情況下我們是根據已知條件來推算結果,而最大似然估計是已經知道了結果,然后尋求使該結果出現的可能性最大的條件,以此作為估計值。比如,如果其他條件一定的話,抽煙者發生肺癌的危險時不抽煙者的5倍,那么如果現在我已經知道有個人是肺癌,我想問你這個人抽煙還是不抽煙。你怎么判斷?你可能對這個人一無所知,你所知道的只有一件事,那就是抽煙更容易發生肺癌,那么你會猜測這個人不抽煙嗎?我相信你更有可能會說,這個人抽煙。為什么?這就是“最大可能”,我只能說他“最有可能”是抽煙的,“他是抽煙的”這一估計值才是“最有可能”得到“肺癌”這樣的結果。這就是最大似然估計。
好了,極大似然估計就講到這,總結一下:
極大似然估計,只是一種概率論在統計學的應用,它是參數估計的方法之一。說的是已知某個隨機樣本滿足某種概率分布,但是其中具體的參數不清楚,參數估計就是通過若干次試驗,觀察其結果,利用結果推出參數的大概值。最大似然估計是建立在這樣的思想上:已知某個參數能使這個樣本出現的概率最大,我們當然不會再去選擇其他小概率的樣本,所以干脆就把這個參數作為估計的真實值。
求最大似然函數估計值的一般步驟:
(1)寫出似然函數;
(2)對似然函數取對數,并整理;
(3)求導數,令導數為0,得到似然方程;
(4)解似然方程,得到的參數即為所求;
?
最大似然譯碼算法在LTE上的應用
假定調制星座圖中的所有信號都是等概的,最大似然譯碼器對所有可能的見,和妥2值,從信號調制星座圖中選擇一對信號(二。,見2)使下面的距離量度最小
d2 r1,h1x 1+h2x 2 +d2 r2,?h1x 2?+h2x 1? =|h1?h1x 1?h2x 2|2+|r2,+h1x 2??h2x 1?|2
(1)
化簡得最大似然譯碼判決準則為:
x 1,x 2 =argmin(x 1,x 2)?C(|h1|2+|h2|2?1)(|x1|2+|x 2|2)+d2 x1,x 1 +d2 x2,x 2
(2)
上式中:C為調制符號對(x 1,x 2)所有可能的集合; x 1和x 2是通過合并接收信號和信道狀態信息構造產生的兩個判決統計。統計結果可以表示為
x1=h1?r1+h1r2?(3)
x2=h2?r1?h1r2? (4)
將式(3)和式(4)中的r1和r2分別代人式(5)中,統計結果可以表示為
x1=(|h1|2+ h2|2 x1+h1?n1+h2n2? (5)
x2=(|h1|2+ h2|2 x2?h1n2?+h2?n1 (6)
對于給定信道實現h1和h2而言,統計結果見xi(i=1,2)僅僅是xi(i=1,2)的函數,因此,可以將最大似然譯碼準則式(4)分為對于x1和x2的2個獨立譯碼算法,即
x 1=argminx2∈S(|h1|2+|h2|2?1)×|x 1|2+d2 x1,x 1 (7)
和
x 2=argminx2∈S(|h1|2+|h2|2?1)×|x 2|2+d2 x2,x 2 (8)
對于M-PSK信號星座圖而言,在給定信號衰落系數的前提下,(|h1|2+|h2|2?1)×|x i|2(i=1,2)對于所有信號都是恒定的,因此可以將式(7)和式 (8)的判決準則進一步簡化為
x 1=argminx2∈S(x1,x 1)=argminx2∈S|h1?r1+h2r1??x 1|2
x 2=argminx2∈S(x2,x 2)=argminx2∈S|h2?r1?h1r2??x2|2
上述最大似然檢測算法可以推廣到多個接收天線的情況。
- 第 1 頁:最大似然檢測算法認識與理解
- 第 2 頁:最大似然估計學習總結
本文導航
非常好我支持^.^
(162) 93.6%
不好我反對
(11) 6.4%
相關閱讀:
- [電子說] 智慧礦山ai算法系列解析 堵料檢測算法功能優勢 2023-09-28
- [工業控制] 基于改進FCOS的表面缺陷檢測算法 2023-09-28
- [電子說] 淺談圖像處理-harris角點檢測算法 2023-09-22
- [電子說] 更深層地理解深偽技術 2023-09-11
- [電子說] 大學畢業設計一席談之四十一 壓電信號的睡眠檢測算法(11)完善程序 2023-08-29
- [汽車電子] 基于Transformer的目標檢測算法難點 2023-08-24
- [電子說] 掌握基于Transformer的目標檢測算法的3個難點 2023-08-22
- [汽車電子] 基于Transformer的目標檢測算法 2023-08-16
( 發表人:李倩 )
