編者按：和Piotr Skalski一起，基于NumPy手寫神經(jīng)網(wǎng)絡(luò)，通過親自動手實(shí)踐，加深對神經(jīng)網(wǎng)絡(luò)內(nèi)部機(jī)制的理解。

Keras、TensorFlow、PyTorch等高層框架讓我們可以快速搭建復(fù)雜模型。然而，花一點(diǎn)時(shí)間了解下底層概念是值得的。前不久我發(fā)過一篇文章，以簡單的方式解釋了神經(jīng)網(wǎng)絡(luò)是如何工作的。但這是一篇高度理論性的文章，主要以數(shù)學(xué)為主（數(shù)學(xué)是神經(jīng)網(wǎng)絡(luò)超能力的來源）。我打算以實(shí)踐的方式繼續(xù)這一主題，在這篇文章中，我們將嘗試僅僅基于NumPy創(chuàng)建一個(gè)可以工作的神經(jīng)網(wǎng)絡(luò)。最后，我們將測試一下創(chuàng)建的模型——用它來解決簡單的分類問題，并和基于Keras搭建的神經(jīng)網(wǎng)絡(luò)比較一下。

顯然，今天的文章會包含很多Python代碼，我希望你不會因此覺得枯燥。我同時(shí)也把文中所有的代碼發(fā)在GitHub上：SkalskiP/ILearnDeepLearning.py

概覽

在開始編程之前，先讓我們準(zhǔn)備一份基本的路線圖。我們的目標(biāo)是創(chuàng)建一個(gè)特定架構(gòu)（層數(shù)、層大小、激活函數(shù)）的密集連接神經(jīng)網(wǎng)絡(luò)。然后訓(xùn)練這一神經(jīng)網(wǎng)絡(luò)并做出預(yù)測。

上面的示意圖展示了訓(xùn)練網(wǎng)絡(luò)時(shí)進(jìn)行的操作，以及單次迭代不同階段需要更新和讀取的參數(shù)。

初始化神經(jīng)網(wǎng)絡(luò)層

讓我們從初始化每一層的權(quán)重矩陣W和偏置向量b開始。下圖展示了網(wǎng)絡(luò)層l的權(quán)重矩陣和偏置向量，其中，上標(biāo)[l]表示當(dāng)前層的索引，n表示給定層中的神經(jīng)元數(shù)量。

我們的程序也將以類似的列表形式描述神經(jīng)網(wǎng)絡(luò)架構(gòu)。列表的每一項(xiàng)是一個(gè)字典，描述單個(gè)網(wǎng)絡(luò)層的基本參數(shù)：input_dim是網(wǎng)絡(luò)層輸入的信號向量的大小，output_dim是網(wǎng)絡(luò)層輸出的激活向量的大小，activation是網(wǎng)絡(luò)層所用的激活函數(shù)。

nn_architecture = [

{"input_dim": 2, "output_dim": 4, "activation": "relu"},

{"input_dim": 4, "output_dim": 6, "activation": "relu"},

{"input_dim": 6, "output_dim": 6, "activation": "relu"},

{"input_dim": 6, "output_dim": 4, "activation": "relu"},

{"input_dim": 4, "output_dim": 1, "activation": "sigmoid"},

]

如果你熟悉這一主題，你的腦海中大概已經(jīng)回蕩起焦急的聲音：“喂喂！搞錯(cuò)了！這里有些是不必要的……”這一次，你內(nèi)心的聲音是對的，一個(gè)網(wǎng)絡(luò)層的輸出向量同時(shí)也是下一層的輸入，所以其實(shí)只用列出兩者之一就夠了。不過，我故意使用這樣的表示法，使每一層的格式保持一致，也讓初次接觸這一主題的人更容易理解代碼。

def init_layers(nn_architecture, seed = 99):

np.random.seed(seed)

number_of_layers = len(nn_architecture)

params_values = {}

for idx, layer in enumerate(nn_architecture):

layer_idx = idx + 1

layer_input_size = layer["input_dim"]

layer_output_size = layer["output_dim"]

params_values['W' + str(layer_idx)] = np.random.randn(

layer_output_size, layer_input_size) * 0.1

params_values['b' + str(layer_idx)] = np.random.randn(

layer_output_size, 1) * 0.1

return params_values

上面的代碼初始化了網(wǎng)絡(luò)層的參數(shù)。注意我們用隨機(jī)的小數(shù)字填充矩陣W和向量b。這并不是偶然的。權(quán)重值無法使用相同的數(shù)字初始化，否則會造成破壞性的對稱問題。基本上，如果權(quán)重都一樣，不管輸入X是什么，隱藏層的所有單元也都一樣。這樣，我們就會陷入初始狀態(tài)，不管訓(xùn)練多久，網(wǎng)絡(luò)多深，都無望擺脫。線性代數(shù)不會原諒我們。

小數(shù)值增加了算法的效率。我們可以看看下面的sigmoid函數(shù)圖像，大數(shù)值處的函數(shù)圖像幾乎是扁平的，這會對神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)速度造成顯著影響。所有參數(shù)使用小隨機(jī)數(shù)是一個(gè)簡單的方法，但它保證了算法有一個(gè)足夠好的開始。

激活函數(shù)

激活函數(shù)只需一行代碼就可以定義，但它們給神經(jīng)網(wǎng)絡(luò)帶來了非線性和所需的表達(dá)力。“沒有它們，神經(jīng)網(wǎng)絡(luò)將變成線性函數(shù)的組合，也就是單個(gè)線性函數(shù)。”激活函數(shù)有很多種，但在這個(gè)項(xiàng)目中，我決定使用其中兩種——sigmoid和ReLU。為了同時(shí)支持前向傳播和反向傳播，我們還需要準(zhǔn)備好它們的導(dǎo)數(shù)。

def sigmoid(Z):

return1/(1+np.exp(-Z))

def relu(Z):

return np.maximum(0,Z)

def sigmoid_backward(dA, Z):

sig = sigmoid(Z)

return dA * sig * (1 - sig)

def relu_backward(dA, Z):

dZ = np.array(dA, copy = True)

dZ[Z <= 0] = 0;

return dZ;

前向傳播

我們設(shè)計(jì)的神經(jīng)網(wǎng)絡(luò)有一個(gè)簡單的架構(gòu)。輸入矩陣X傳入網(wǎng)絡(luò)，沿著隱藏單元傳播，最終得到預(yù)測向量Y_hat。為了讓代碼更易讀，我將前向傳播拆分成兩個(gè)函數(shù)——單層前向傳播，和整個(gè)神經(jīng)網(wǎng)絡(luò)前向傳播。

def single_layer_forward_propagation(A_prev, W_curr, b_curr, activation="relu"):

Z_curr = np.dot(W_curr, A_prev) + b_curr

if activation is"relu":

activation_func = relu

elif activation is"sigmoid":

activation_func = sigmoid

else:

raiseException('Non-supported activation function')

return activation_func(Z_curr), Z_curr

這部分代碼大概是最直接，最容易理解的。給定來自上一層的輸入信號，我們計(jì)算仿射變換Z，接著應(yīng)用選中的激活函數(shù)。基于NumPy，我們可以對整個(gè)網(wǎng)絡(luò)層和整批樣本一下子進(jìn)行矩陣操作，無需迭代，這大大加速了計(jì)算。除了計(jì)算結(jié)果外，函數(shù)還返回了一個(gè)反向傳播時(shí)需要用到的中間值Z。

基于單層前向傳播函數(shù)，編寫整個(gè)前向傳播步驟很容易。這是一個(gè)略微復(fù)雜一點(diǎn)的函數(shù)，它的角色不僅是進(jìn)行預(yù)測，還包括組織中間值。

def full_forward_propagation(X, params_values, nn_architecture):

memory = {}

A_curr = X

for idx, layer in enumerate(nn_architecture):

layer_idx = idx + 1

A_prev = A_curr

activ_function_curr = layer["activation"]

W_curr = params_values["W" + str(layer_idx)]

b_curr = params_values["b" + str(layer_idx)]

A_curr, Z_curr = single_layer_forward_propagation(A_prev, W_curr, b_curr, activ_function_curr)

memory["A" + str(idx)] = A_prev

memory["Z" + str(layer_idx)] = Z_curr

return A_curr, memory

損失函數(shù)

損失函數(shù)可以監(jiān)測進(jìn)展，確保我們向著正確的方向移動。“一般來說，損失函數(shù)是為了顯示我們離‘理想’解答還有多遠(yuǎn)。”損失函數(shù)根據(jù)我們計(jì)劃解決的問題而選用，Keras之類的框架提供了很多選項(xiàng)。因?yàn)槲矣?jì)劃將神經(jīng)網(wǎng)絡(luò)用于二元分類問題，我決定使用交叉熵：

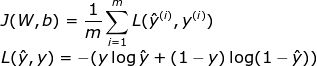
為了取得更多關(guān)于學(xué)習(xí)過程的信息，我決定另外實(shí)現(xiàn)一個(gè)計(jì)算精確度的函數(shù)。

def get_cost_value(Y_hat, Y):

m = Y_hat.shape[1]

cost = -1 / m * (np.dot(Y, np.log(Y_hat).T) + np.dot(1 - Y, np.log(1 - Y_hat).T))

return np.squeeze(cost)

def get_accuracy_value(Y_hat, Y):

Y_hat_ = convert_prob_into_class(Y_hat)

return (Y_hat_ == Y).all(axis=0).mean()

反向傳播

不幸的是，很多缺乏經(jīng)驗(yàn)的深度學(xué)習(xí)愛好者都覺得反向傳播很嚇人，難以理解。微積分和線性代數(shù)的組合經(jīng)常會嚇退那些沒有經(jīng)過扎實(shí)的數(shù)學(xué)訓(xùn)練的人。所以不要過于擔(dān)心你現(xiàn)在還不能理解這一切。相信我，我們都經(jīng)歷過這個(gè)過程。

def single_layer_backward_propagation(dA_curr, W_curr, b_curr, Z_curr, A_prev, activation="relu"):

m = A_prev.shape[1]

if activation is"relu":

backward_activation_func = relu_backward

elif activation is"sigmoid":

backward_activation_func = sigmoid_backward

else:

raiseException('Non-supported activation function')

dZ_curr = backward_activation_func(dA_curr, Z_curr)

dW_curr = np.dot(dZ_curr, A_prev.T) / m

db_curr = np.sum(dZ_curr, axis=1, keepdims=True) / m

dA_prev = np.dot(W_curr.T, dZ_curr)

return dA_prev, dW_curr, db_curr

人們經(jīng)常搞混反向傳播和梯度下降，但事實(shí)上它們不一樣。前者是為了高效地計(jì)算梯度，后者則是為了基于計(jì)算出的梯度進(jìn)行優(yōu)化。在神經(jīng)網(wǎng)絡(luò)中，我們計(jì)算損失函數(shù)在參數(shù)上的梯度，但反向傳播可以用來計(jì)算任何函數(shù)的導(dǎo)數(shù)。反向傳播算法的精髓在于遞歸地使用求導(dǎo)的鏈?zhǔn)椒▌t，通過組合導(dǎo)數(shù)已知的函數(shù)，計(jì)算函數(shù)的導(dǎo)數(shù)。下面的公式描述了單個(gè)網(wǎng)絡(luò)層上的反向傳播過程。由于本文的重點(diǎn)在實(shí)際實(shí)現(xiàn)，所以我將省略求導(dǎo)過程。從公式上我們可以很明顯地看到，為什么我們需要在前向傳播時(shí)記住中間層的A、Z矩陣的值。

和前向傳播一樣，我決定將計(jì)算拆分成兩個(gè)函數(shù)。之前給出的是單個(gè)網(wǎng)絡(luò)層的反向傳播函數(shù)，基本上就是以NumPy方式重寫上面的數(shù)學(xué)公式。而定義完整反向傳播過程的函數(shù)，主要是讀取、更新三個(gè)字典中的值。

def full_backward_propagation(Y_hat, Y, memory, params_values, nn_architecture):

grads_values = {}

m = Y.shape[1]

Y = Y.reshape(Y_hat.shape)

dA_prev = - (np.divide(Y, Y_hat) - np.divide(1 - Y, 1 - Y_hat));

for layer_idx_prev, layer in reversed(list(enumerate(nn_architecture))):

layer_idx_curr = layer_idx_prev + 1

activ_function_curr = layer["activation"]

dA_curr = dA_prev

A_prev = memory["A" + str(layer_idx_prev)]

Z_curr = memory["Z" + str(layer_idx_curr)]

W_curr = params_values["W" + str(layer_idx_curr)]

b_curr = params_values["b" + str(layer_idx_curr)]

dA_prev, dW_curr, db_curr = single_layer_backward_propagation(

dA_curr, W_curr, b_curr, Z_curr, A_prev, activ_function_curr)

grads_values["dW" + str(layer_idx_curr)] = dW_curr

grads_values["db" + str(layer_idx_curr)] = db_curr

return grads_values

基于單個(gè)網(wǎng)絡(luò)層的反向傳播函數(shù)，我們從最后一層開始迭代計(jì)算所有參數(shù)上的導(dǎo)數(shù)，并最終返回包含所需梯度的python字典。

更新參數(shù)值

反向傳播是為了計(jì)算梯度，以根據(jù)梯度進(jìn)行優(yōu)化，更新網(wǎng)絡(luò)的參數(shù)值。為了完成這一任務(wù)，我們將使用兩個(gè)字典作為函數(shù)參數(shù)：params_values，其中保存了當(dāng)前參數(shù)值；grads_values，其中保存了用于更新參數(shù)值所需的梯度信息。現(xiàn)在我們只需在每個(gè)網(wǎng)絡(luò)層上應(yīng)用以下等式即可。這是一個(gè)非常簡單的優(yōu)化算法，但我決定使用它作為更高級的優(yōu)化算法的起點(diǎn)（大概會是我下一篇文章的主題）。

def update(params_values, grads_values, nn_architecture, learning_rate):

for idx, layer in enumerate(nn_architecture):

layer_idx = idx + 1

params_values["W" + str(layer_idx)] -= learning_rate * grads_values["dW" + str(layer_idx)]

params_values["b" + str(layer_idx)] -= learning_rate * grads_values["db" + str(layer_idx)]

return params_values;

整合一切

萬事俱備只欠東風(fēng)。最困難的部分已經(jīng)完成了——我們已經(jīng)準(zhǔn)備好了所需的函數(shù)，現(xiàn)在只需以正確的順序把它們放到一起。

def train(X, Y, nn_architecture, epochs, learning_rate):

params_values = init_layers(nn_architecture, 2)

cost_history = []

accuracy_history = []

for i in range(epochs):

Y_hat, cashe = full_forward_propagation(X, params_values, nn_architecture)

cost = get_cost_value(Y_hat, Y)

cost_history.append(cost)

accuracy = get_accuracy_value(Y_hat, Y)

accuracy_history.append(accuracy)

grads_values = full_backward_propagation(Y_hat, Y, cashe, params_values, nn_architecture)

params_values = update(params_values, grads_values, nn_architecture, learning_rate)

return params_values, cost_history, accuracy_history

大衛(wèi)對戰(zhàn)歌利亞

該是看看我們的模型能不能解決一個(gè)簡單的分類問題的時(shí)候了。我生成了一個(gè)包含兩個(gè)分類的數(shù)據(jù)點(diǎn)的數(shù)據(jù)集，如下圖所示。

作為對比，我用高層框架Keras搭建了一個(gè)模型。兩個(gè)模型采用相同的架構(gòu)和學(xué)習(xí)率。不過這仍然是一場不公平的較量，因?yàn)槲覀兊哪Ｐ陀玫亩际亲詈唵蔚姆桨浮Ｗ罱K，基于NumPy和Keras的模型在測試集上都取得了類似的精確度（95%）。不過，我們的模型收斂的速度要慢很多倍。在我看來，這主要是因?yàn)槲覀兊哪Ｐ腿狈η‘?dāng)?shù)膬?yōu)化算法。

再見

希望我的文章拓展了你的視野，增加了你對神經(jīng)網(wǎng)絡(luò)內(nèi)部運(yùn)作機(jī)制的理解——這將是對我投入精力撰寫本文的最好回報(bào)。我在編寫代碼和說明的時(shí)候也學(xué)到了很多東西，親自動手實(shí)踐能讓你學(xué)到很多東西。

如你有任何疑問，或者找到了代碼中的錯(cuò)誤，請留言告知。如果你喜歡這篇文章，可以在Twitter（PiotrSkalski92）和Medium（piotr.skalski92）上關(guān)注我，也可以上GitHub（SkalskiP）和Kaggle（skalskip）查看我的其他項(xiàng)目。本文是“神經(jīng)網(wǎng)絡(luò)的奧秘”系列的第三篇，如果你還沒有讀過前兩篇，可以看一下https://towardsdatascience.com/preventing-deep-neural-network-from-overfitting-953458db800a

保持好奇心！