▌概述

本文主要介紹一種降維方法，PCA（Principal Component Analysis，主成分分析）。降維致力于解決三類問題：

1.降維可以緩解維度災難問題；

2.降維可以在壓縮數據的同時讓信息損失最小化；

3.理解幾百個維度的數據結構很困難，兩三個維度的數據通過可視化更容易理解。

下面，將從簡介、計算步驟、應用三方面進行理解PCA的降維作用。

▌PCA簡介

在理解特征提取與處理時，涉及高維特征向量的問題往往容易陷入維度災難。隨著數據集維度的增加，算法學習需要的樣本數量呈指數級增加。有些應用中，遇到這樣的大數據是非常不利的，而且從大數據集中學習需要更多的內存和處理能力。另外，隨著維度的增加，數據的稀疏性會越來越高。在高維向量空間中探索同樣的數據集比在同樣稀疏的數據集中探索更加困難。

主成分分析也稱為卡爾胡寧-勒夫變換（Karhunen-Loeve Transform），是一種用于探索高維數據結構的技術。PCA通常用于高維數據集的探索與可視化。還可以用于數據壓縮，數據預處理等。PCA可以把可能具有相關性的高維變量合成線性無關的低維變量，稱為主成分（ principal components）。新的低維數據集會盡可能的保留原始數據的變量。

PCA將數據投射到一個低維子空間實現降維。例如，二維數據集降維就是把點投射成一條線，數據集的每個樣本都可以用一個值表示，不需要兩個值。三維數據集可以降成二維，就是把變量映射成一個平面。一般情況下，nn維數據集可以通過映射降成kk維子空間，其中k≤n。

假如你是一本養花工具宣傳冊的攝影師，你正在拍攝一個水壺。水壺是三維的，但是照片是二維的，為了更全面的把水壺展示給客戶，你需要從不同角度拍幾張圖片。下圖是你從四個方向拍的照片：

第一張圖里水壺的背面可以看到，但是看不到前面。第二張圖是拍前面，可以看到壺嘴，這張圖可以提供了第一張圖缺失的信息，但是壺把看不到了。從第三張俯視圖里無法看出壺的高度。第四張圖是你真正想要的，水壺的高度，頂部，壺嘴和壺把都清晰可見。

PCA的設計理念與此類似，它可以將高維數據集映射到低維空間的同時，盡可能的保留更多變量。PCA旋轉數據集與其主成分對齊，將最多的變量保留到第一主成分中。假設我們有下圖所示的數據集：

數據集看起來像一個從原點到右上角延伸的細長扁平的橢圓。要降低整個數據集的維度，我們必須把點映射成一條線。下圖中的兩條線都是數據集可以映射的，映射到哪條線樣本變化最大？

顯然，樣本映射到黑色虛線的變化比映射到紅色點線的變化要大的多。實際上，這條黑色虛線就是第一主成分。第二主成分必須與第一主成分正交，也就是說第二主成分必須是在統計學上獨立的，會出現在與第一主成分垂直的方向，如下圖所示：

后面的每個主成分也會盡量多的保留剩下的變量，唯一的要求就是每一個主成分需要和前面的主成分正交。 現在假設數據集是三維的，散點圖看起來像是沿著一個軸旋轉的圓盤。

這些點可以通過旋轉和變換使圓盤完全變成二維的。現在這些點看著像一個橢圓，第三維上基本沒有變量，可以被忽略。當數據集不同維度上的方差分布不均勻的時候，PCA最有用。（如果是一個球殼形數據集，PCA不能有效的發揮作用，因為各個方向上的方差都相等；沒有丟失大量的信息維度一個都不能忽略）。

▌PCA的計算步驟

在介紹PCA的運行步驟之前，有一些術語需要說明一下。

方差，協方差和協方差矩陣（對此概念不是很理解可以參考附錄鏈接）

如何通俗易懂地解釋「協方差」與「相關系數」的概念？中“GRAYLAMB”的回答。 （https://www.zhihu.com/question/20852004）

方差（Variance）是度量一組數據的分散程度。方差是各個樣本與樣本均值的差的平方和的均值：

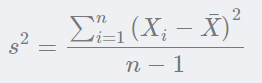
協方差（Covariance）是度量兩個變量的變動的同步程度，也就是度量兩個變量線性相關性程度。

如果兩個變量的協方差為0，則統計學上認為二者線性無關。注意兩個無關的變量并非完全獨立，只是沒有線性相關性而已。計算公式如下：

如果協方差大于0表示一個變量增大是另一個變量也會增大，即正相關，協方差小于0表示一個變量增大是另一個變量會減小，即負相關。

協方差矩陣（Covariance matrix）由數據集中兩兩變量的協方差組成。矩陣的第(i,j)(i,j)個元素是數據集中第ii和第jj個元素的協方差。例如，三維數據的協方差矩陣如下所示：

讓我們計算下表數據的協方差矩陣：

可以有python中的numpy包計算均值和協方差：

importnumpyasnpX=[[2,0,-1.4],[2.2,0.2,-1.5],[2.4,0.1,-1],[1.9,0,-1.2]]print(np.mean(X,axis=0))print(np.cov(np.array(X).T))

得到三個變量的樣本均值分別是2.125，0.075和-1.275；協方差矩陣為：

▌特征向量和特征值

（可以直觀的理解：“特征向量是坐標軸，特征值是坐標”）

向量是具有大小（magnitude）和方向（direction）的幾何概念。

特征向量（eigenvector）是由滿足如下公式的矩陣得到的一個非零向量：

其中，是特征向量，A是方陣，λ是特征值。經過A變換之后，特征向量的方向保持不變，只是其大小發生了特征值倍數的變化。也就是說，一個特征向量左乘一個矩陣之后等于等比例放縮（scaling）特征向量。德語單詞eigen的意思是“屬于…或…專有（ belonging to or peculiar to）”；矩陣的特征向量是屬于并描述數據集結構的向量。

特征向量和特征值只能由方陣得出，且并非所有方陣都有特征向量和特征值。如果一個矩陣有特征向量和特征值，那么它的每個維度都有一對特征向量和特征值。矩陣的主成分是由其協方差矩陣的特征向量，按照對應的特征值大小排序得到的。最大的特征值就是第一主成分，第二大的特征值就是第二主成分，以此類推。

讓我們來計算下面矩陣的特征向量和特征值：

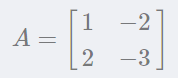
根據前面的公式AA乘以特征向量，必然等于特征值乘以特征向量。我們建立特征方程求解：

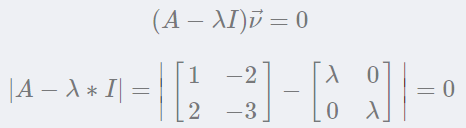
從特征方程可以看出，矩陣與單位矩陣和特征值乘積的矩陣行列式為0，即：

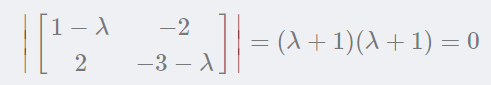
矩陣的兩個特征值都等于-1。現在再用特征值來解特征向量。 把λ=?1帶入：

得：

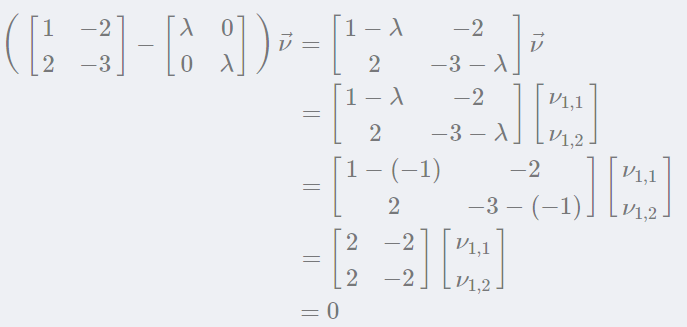
所以有：

任何滿足方程的非零向量（取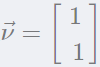）都可以作為特征向量：?

PCA需要單位特征向量，也就是L2范數等于1的特征向量。?

于是單位特征向量是：

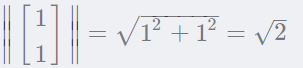
于是單位特征向量是：

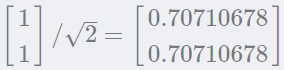
這里可以通過numpy檢驗手算的特征向量是否正確。eig函數返回特征值和特征向量的元組：

importnumpyasnpw,v=np.linalg.eig(np.array([[1,-2],[2,-3]]))print('特征值：{} 特征向量：{}'.format(w,v))

輸出（這里特征值不同為1，是由于python編譯器對浮點數據精度要求所致）：

特征值：[-0.99999998 -1.00000002]

特征向量：[[ 0.70710678 0.70710678] [ 0.70710678 0.70710678]]

▌用PCA降維

讓我們用PCA方法把下表二維數據降成一維：

PCA第一步是用樣本數據減去樣本均值：

然后，我們計算數據的主成分。前面介紹過，矩陣的主成分是其協方差矩陣的特征向量按照對應的特征值大小排序得到的。主成分可以通過兩種方法計算：第一種方法是計算數據協方差矩陣。因為協方差矩陣是方陣，所以我們可以用前面的方法計算特征值和特征向量。第二種方法是用數據矩陣的奇異值分解（singular value decomposition）來找協方差矩陣的特征向量和特征值的平方根。我們先介紹第一種方法，然后介紹scikit-learn的PCA實現，也就是第二種方法。上述數據集的解釋變量協方差矩陣如下：

用前面介紹過的方法，特征值是1.25057433和0.03398123，單位特征向量是：

下面我們把數據映射到主成分上。第一主成分是最大特征值對應的特征向量，因此我們要建一個轉換矩陣，它的每一列都是主成分的特征向量。如果我們要把5維數據降成3維，那么我們就要用一個3維矩陣做轉換矩陣。在本例中，我們將把我們的二維數據映射成一維，因此我們只需要用特征向量中的第一主成分作為轉換矩陣。最后，我們用數據矩陣右乘轉換矩陣。下面就是第一主成分映射的結果：

通過numpy包中的矩陣調用實現過程如下：

importnumpyasnpx=np.mat([[0.9,2.4,1.2,0.5,0.3,1.8,0.5,0.3,2.5,1.3],[1,2.6,1.7,0.7,0.7,1.4,0.6,0.6,2.6,1.1]])x=x.TT=x-x.mean(axis=0)C=np.cov(x.T)w,v=np.linalg.eig(C)v_=np.mat(v[:,0])#每個特征值對應的是特征矩陣的每個列向量v_=v_.T#默認以行向量保存，轉換成公式中的列向量形式y=T*v_print(y)

分割線==================

▌PCA的運用

高維數據可視化

二維或三維數據更容易通過可視化發現模式。一個高維數據集是無法用圖形表示的，但是我們可以通過降維方法把它降成二維或三維數據來可視化。 Fisher1936年收集了三種鳶尾花分別50個樣本數據（Iris Data）：Setosa、Virginica、Versicolour。解釋變量是花瓣（petals）和萼片（sepals）長度和寬度的測量值，響應變量是花的種類。鳶尾花數據集經常用于分類模型測試，scikit-learn中也有。讓我們把iris數據集降成方便可視化的二維數據：

%matplotlibinlineimportmatplotlib.pyplotaspltfromsklearn.decompositionimportPCAfromsklearn.datasetsimportload_iris

首先，我們導入鳶尾花數據集和PCA估計器。PCA類把主成分的數量作為超參數，和其他估計器一樣，PCA也用fit_transform()返回降維的數據矩陣：

data=load_iris()y=data.targetX=data.datapca=PCA(n_components=2)reduced_X=pca.fit_transform(X)

最后，我們把圖形畫出來：

red_x,red_y=[],[]blue_x,blue_y=[],[]green_x,green_y=[],[]foriinrange(len(reduced_X)):ify[i]==0:red_x.append(reduced_X[i][0])red_y.append(reduced_X[i][1])elify[i]==1:blue_x.append(reduced_X[i][0])blue_y.append(reduced_X[i][1])else:green_x.append(reduced_X[i][0])green_y.append(reduced_X[i][1])plt.scatter(red_x,red_y,c='r',marker='x')plt.scatter(blue_x,blue_y,c='b',marker='D')plt.scatter(green_x,green_y,c='g',marker='.')plt.show()

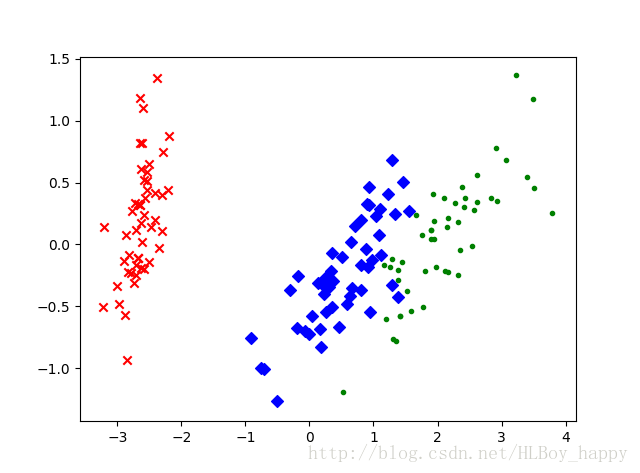
降維的數據如上圖所示。每個數據集中三個類都用不同的符號標記。從這個二維數據圖中可以明顯看出，有一個類與其他兩個重疊的類完全分離。這個結果可以幫助我們選擇分類模型。

臉部識別

現在讓我們用PCA來解決一個臉部識別問題。臉部識別是一個監督分類任務，用于從照片中認出某個人。本例中，我們用劍橋大學AT&T實驗室的Our Database of Faces數據集（http://www.cl.cam.ac.uk/Research/DTG/attarchive/pub/data/att_faces.zip），這個數據集包含40個人每個人10張照片。這些照片是在不同的光照條件下拍攝的，每張照片的表情也不同。照片都是黑白的，尺寸為92 x 112像素。雖然這些圖片都不大，但是每張圖片的按像素強度排列的特征向量也有（92 x 112=）10304維。這些高維數據的訓練可能需要很多樣本才能避免擬合過度。而我們樣本量并不大，所有我們用PCA計算一些主成分來表示這些照片。

我們可以把照片的像素強度矩陣轉換成向量，然后用所有的訓練照片的向量建一個矩陣。每個照片都是數據集主成分的線性組合。在臉部識別理論中，這些主成分稱為特征臉（eigenfaces）。特征臉可以看成是臉部的標準化組成部分。數據集中的每張臉都可以通過一些標準臉的組合生成出來，或者說是最重要的特征臉線性組合的近似值。

fromosimportwalk,pathimportnumpyasnpimportmahotasasmhfromsklearn.cross_validationimporttrain_test_splitfromsklearn.cross_validationimportcross_val_scorefromsklearn.preprocessingimportscalefromsklearn.decompositionimportPCAfromsklearn.linear_modelimportLogisticRegressionfromsklearn.metricsimportclassification_reportX=[]y=[]

下面我們把照片導入Numpy數組，然后把它們的像素矩陣轉換成向量：

fordir_path,dir_names,file_namesinwalk('C:/Users/HLB/Desktop/firstblog/att_faces/'):#walk()函數內存放的是數據的絕對路徑，同時注意斜杠的方向。forfninfile_names:iffn[-3:]=='pgm':image_filename=path.join(dir_path,fn)X.append(scale(mh.imread(image_filename,as_grey=True).reshape(10304).astype('float32')))y.append(dir_path)X=np.array(X)

然后，我們用交叉檢驗建立訓練集和測試集，在訓練集上用PCA：

X_train,X_test,y_train,y_test=train_test_split(X,y)pca=PCA(n_components=150)

我們把所有樣本降到150維，然后訓練一個邏輯回歸分類器。數據集包括40個類；scikit-learn底層會自動用one versus all策略創建二元分類器：

X_train_reduced=pca.fit_transform(X_train)X_test_reduced=pca.transform(X_test)print('訓練集數據的原始維度是：{}'.format(X_train.shape))print('PCA降維后訓練集數據是：{}'.format(X_train_reduced.shape))classifier=LogisticRegression()accuracies=cross_val_score(classifier,X_train_reduced,y_train)

訓練集數據的原始維度是：(300, 10304) PCA降維后訓練集數據是：(300, 150)

最后，我們用交叉驗證和測試集評估分類器的性能。分類器的平均綜合評價指標（F1 score）是0.88，但是需要花費更多的時間訓練，在更多訓練實例的應用中可能會更慢。

print('交叉驗證準確率是：{} {}'.format(np.mean(accuracies),accuracies))classifier.fit(X_train_reduced,y_train)predictions=classifier.predict(X_test_reduced)print(classification_report(y_test,predictions))

最終的分析結果：

交叉驗證準確率是：0.829757290513[0.830357140.833333330.8255814]precisionrecallf1-scoresupportC:/Users/HLB/Desktop/firstblog/att_faces/s11.001.001.001C:/Users/HLB/Desktop/firstblog/att_faces/s101.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s111.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s121.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s131.001.001.004C:/Users/HLB/Desktop/firstblog/att_faces/s141.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s151.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s161.000.750.864C:/Users/HLB/Desktop/firstblog/att_faces/s171.001.001.004C:/Users/HLB/Desktop/firstblog/att_faces/s181.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s191.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s21.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s201.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s211.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s221.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s231.001.001.004C:/Users/HLB/Desktop/firstblog/att_faces/s241.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s251.001.001.004C:/Users/HLB/Desktop/firstblog/att_faces/s261.001.001.005C:/Users/HLB/Desktop/firstblog/att_faces/s270.501.000.671C:/Users/HLB/Desktop/firstblog/att_faces/s281.000.670.803C:/Users/HLB/Desktop/firstblog/att_faces/s291.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s31.001.001.001C:/Users/HLB/Desktop/firstblog/att_faces/s301.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s311.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s321.001.001.001C:/Users/HLB/Desktop/firstblog/att_faces/s331.001.001.001C:/Users/HLB/Desktop/firstblog/att_faces/s341.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s351.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s360.671.000.802C:/Users/HLB/Desktop/firstblog/att_faces/s370.501.000.671C:/Users/HLB/Desktop/firstblog/att_faces/s381.001.001.005C:/Users/HLB/Desktop/firstblog/att_faces/s391.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s41.001.001.001C:/Users/HLB/Desktop/firstblog/att_faces/s401.001.001.001C:/Users/HLB/Desktop/firstblog/att_faces/s51.000.830.916C:/Users/HLB/Desktop/firstblog/att_faces/s61.001.001.003C:/Users/HLB/Desktop/firstblog/att_faces/s71.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s81.001.001.002C:/Users/HLB/Desktop/firstblog/att_faces/s91.001.001.001avg/total0.980.970.97100

▌總結

本文主要介紹PCA降維問題。高維數據不能輕易可視化。估計器訓練高維數據集時，也可能出現維度災難。通過主成分分析法緩解這些問題，將可能解釋變量具有相關性的高維數據集，通過將數據映射到一個低維子空間，降維成一個線性無關的低維數據集。最后拓展用PCA將四維的鳶尾花數據集降成二維數據進行可視化；并將PCA用在一個臉部識別系統。