以下的幾幅圖是我認為在解釋機器學習基本概念時最有啟發(fā)性的條目列表。
1. Test and training error: 為什么低訓練誤差并不總是一件好的事情呢:以模型復雜度為變量的測試及訓練錯誤函數(shù)。
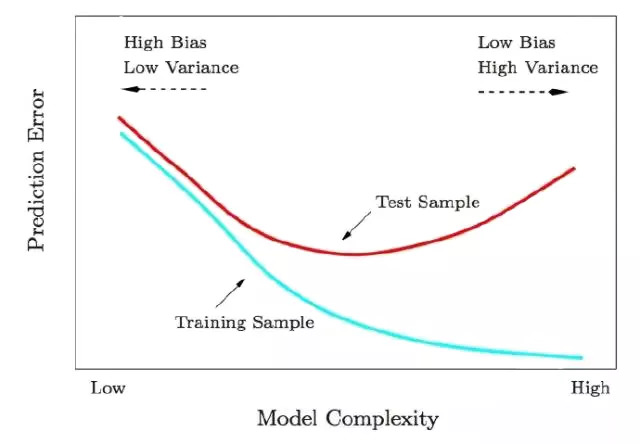
2. Under and overfitting: 低度擬合或者過度擬合的例子。多項式曲線有各種各樣的命令M,以紅色曲線表示,由綠色曲線適應數(shù)據(jù)集后生成。
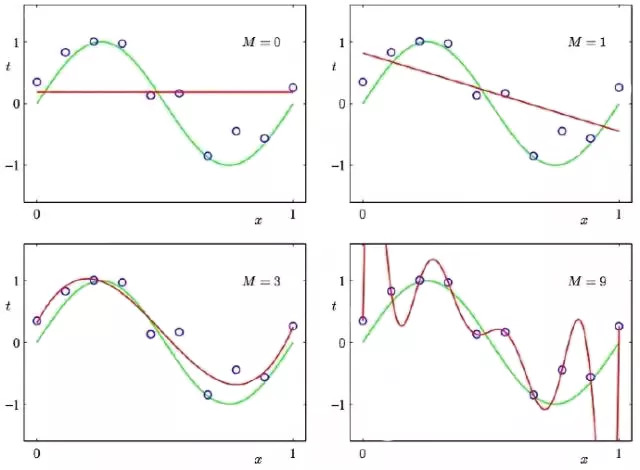
3. Occam’s razor:為什么貝葉斯推理可以具體化奧卡姆剃刀原理。這張圖給了為什么復雜模型原來是小概率事件這個問題一個基本的直觀的解釋。水平軸代表了可能的數(shù)據(jù)集D空間。貝葉斯定理以他們預測的數(shù)據(jù)出現(xiàn)的程度成比例地反饋模型。這些預測被數(shù)據(jù)D上歸一化概率分布量化。數(shù)據(jù)的概率給出了一種模型Hi,P(D|Hi)被稱作支持Hi模型的證據(jù)。一個簡單的模型H1僅可以做到一種有限預測,以P(D|H1)展示;一個更加強大的模型H2,舉例來說,可以比模型H1擁有更加自由的參數(shù),可以預測更多種類的數(shù)據(jù)集。這也表明,無論如何,H2在C1域中對數(shù)據(jù)集的預測做不到像H1那樣強大。假設相等的先驗概率被分配給這兩種模型,之后數(shù)據(jù)集落在C1區(qū)域,不那么強大的模型H1將會是更加合適的模型。
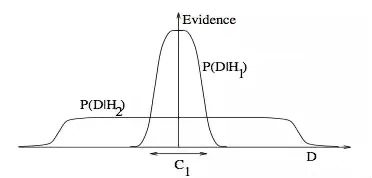
4. Feature combinations:(1)為什么集體相關的特征單獨來看時無關緊要,這也是(2)線性方法可能會失敗的原因。
5. Irrelevant features:為什么無關緊要的特征會損害KNN,聚類,以及其它以相似點聚集的方法。左右的圖展示了兩類數(shù)據(jù)很好地被分離在縱軸上。右圖添加了一條不切題的橫軸,它破壞了分組,并且使得許多點成為相反類的近鄰。
6. Basis functions:非線性的基礎函數(shù)是如何使一個低維度的非線性邊界的分類問題,轉變?yōu)橐粋€高維度的線性邊界問題。Andrew Moore的支持向量機SVM(Support Vector Machine)教程幻燈片中有:一個單維度的非線性帶有輸入x的分類問題轉化為一個2維的線性可分的z=(x,x^2)問題。
7. Discriminative vs. Generative:為什么判別式學習比產生式更加簡單:兩類方法的分類條件的密度舉例,有一個單一的輸入變量x(左圖),連同相應的后驗概率(右圖)。注意到左側的分類條件密度p(x|C1)的模式,在左圖中以藍色線條表示,對后驗概率沒有影響。右圖中垂直的綠線展示了x中的決策邊界,它給出了最小的誤判率。
8. Loss functions:學習算法可以被視作優(yōu)化不同的損失函數(shù):應用于支持向量機中的“鉸鏈”錯誤函數(shù)圖形,以藍色線條表示,為了邏輯回歸,隨著錯誤函數(shù)被因子1/ln(2)重新調整,它通過點(0,1),以紅色線條表示。黑色線條表示誤分,均方誤差以綠色線條表示。
9. Geometry of least squares:帶有兩個預測的最小二乘回歸的N維幾何圖形。結果向量y正交投影到被輸入向量x1和x2所跨越的超平面。投影y^代表了最小二乘預測的向量。
10. Sparsity:為什么Lasso算法(L1正規(guī)化或者拉普拉斯先驗)給出了稀疏的解決方案(比如:帶更多0的加權向量):lasso算法的估算圖像(左)以及嶺回歸算法的估算圖像(右)。展示了錯誤的等值線以及約束函數(shù)。分別的,當紅色橢圓是最小二乘誤差函數(shù)的等高線時,實心的藍色區(qū)域是約束區(qū)域|β1| + |β2| ≤ t以及β12 + β22 ≤ t2。
-
模型
+關注
關注
1文章
3295瀏覽量
49038 -
貝葉斯
+關注
關注
0文章
77瀏覽量
12585 -
機器學習
+關注
關注
66文章
8437瀏覽量
132898
原文標題:【通俗易懂】10幅圖解釋機器學習中的基本概念
文章出處:【微信號:Imgtec,微信公眾號:Imagination Tech】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
相關推薦




 機器學習是什么?10幅圖帶你詳細的了解機器學習
機器學習是什么?10幅圖帶你詳細的了解機器學習










評論