金屬是一種高導(dǎo)電材料,能夠非常好地反射入射的電磁波—光、微波及無線電波。當(dāng)通過 RF 模塊和波動(dòng)光學(xué)模塊模擬頻域電磁波問題時(shí),您可以通過其中的幾個(gè)選項(xiàng)來模擬金屬物體。這里,我們將介紹阻抗、過渡邊界條件和完美電導(dǎo)體邊界條件,并說明每類條件何時(shí)使用。
什么是金屬?
對(duì)于什么是金屬這個(gè)問題,我們可以從用于求解電磁波問題的 Maxwell 控制方程組開始。考慮以下頻域形式的 Maxwell 方程組:
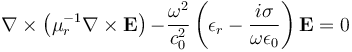
上述方程通過 RF 模塊和波動(dòng)光學(xué)模塊的電磁波,頻域接口求解。方程求解了工作(角)頻率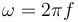 ?下的電場(chǎng)?
?下的電場(chǎng)?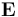 。其他輸入項(xiàng)包括以下材料屬性:?是?相對(duì)磁導(dǎo)率、?是?相對(duì)介電常數(shù),
。其他輸入項(xiàng)包括以下材料屬性:?是?相對(duì)磁導(dǎo)率、?是?相對(duì)介電常數(shù),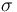 ?是電導(dǎo)率。
?是電導(dǎo)率。
出于本文的討論目的,我們將假設(shè)集膚深度相對(duì)較小且有損耗的材料都是金屬。有損耗材料指任何介電常數(shù)或磁導(dǎo)率為復(fù)數(shù)值、或電導(dǎo)率非零的材料。也就是說,有損耗材料會(huì)向控制方程引入一個(gè)虛數(shù)值項(xiàng)。這會(huì)在材料內(nèi)產(chǎn)生電流,集膚深度是電流進(jìn)入材料內(nèi)深度的測(cè)量指標(biāo)。
工作頻率非零時(shí),電磁感應(yīng)都會(huì)將有損耗材料中的電流推向邊界處。集膚深度是指電流減小到 63% 時(shí)進(jìn)入材料的距離,可以通過以下公式計(jì)算:
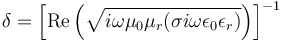
其中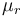 ?和?
?和?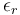 ?都可以是復(fù)數(shù)值。
?都可以是復(fù)數(shù)值。
在極高的頻率(接近光學(xué)波段)下,材料接近等離子共振,我們實(shí)際上會(huì)通過復(fù)數(shù)值介電常數(shù)來表征金屬。但當(dāng)在低于這些頻率下對(duì)金屬進(jìn)行模擬時(shí),我們可以假設(shè)介電常數(shù)為一、磁導(dǎo)率為實(shí)數(shù)值,電導(dǎo)率非常高。因此上述方程可以簡(jiǎn)化為:
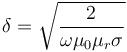
不過在您開始利用 COMSOL Multiphysics 進(jìn)行模擬前,首先應(yīng)計(jì)算或粗略估算所有模擬材料的集膚深度。集膚深度和零件尺寸信息,這兩點(diǎn)將確定能否使用阻抗邊界條件或過渡邊界條件。
阻抗邊界條件
既然已經(jīng)知道了集膚深度,我們希望能將該值與模擬物體的特征尺寸進(jìn)行對(duì)比。有幾種定義方式。根據(jù)具體情況,特征尺寸可以定義為體積與表面積的比值,或模擬物體最薄部分的厚度。
我們假設(shè)一個(gè)的物體;也就是說,物體遠(yuǎn)大于集膚深度。雖然會(huì)有電流進(jìn)入物體內(nèi)部,但集膚效應(yīng)會(huì)將這些電流推到表面上。因此,從模擬的角度來看,我們可以將電流看作在表面上方流動(dòng)。此時(shí)就可以使用阻抗邊界條件,它會(huì)將邊界“背后”的所有材料處理為無限大。從電磁波的角度來看,這一點(diǎn)成立,因?yàn)?img src="http://file.elecfans.com/web1/M00/5C/5A/o4YBAFt07v6Afd53AAAB4HDN93Q794.png" />?說明波不會(huì)穿透物體。
如果集膚深度遠(yuǎn)小于物體,就可以使用阻抗邊界條件。
借助阻抗邊界條件 (IBC),我們可以假定電流完全在表面之上,因此不必再模擬模型金屬域內(nèi)任何部分的 Maxwell 方程組。所以,不必再對(duì)這些域的內(nèi)部進(jìn)行網(wǎng)格剖分,并能顯著減少計(jì)算工作量。此外,IBC 還計(jì)算了由有限電導(dǎo)率造成的損耗。對(duì)于 IBC 適用情況以及與解析結(jié)果的對(duì)比,您可以查看腔體諧振器的 Q 因子和諧振頻率教程案例。
隨著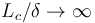 ,IBC 將逐漸更精確;對(duì)于類似球體的光滑物體,即使?
,IBC 將逐漸更精確;對(duì)于類似球體的光滑物體,即使?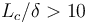 ,它仍能保持精確。對(duì)于類似楔形的鋒利物體,拐角處會(huì)略微不精確,這屬于局部影響,也是向模擬引入尖角后的一個(gè)固有問題。
,它仍能保持精確。對(duì)于類似楔形的鋒利物體,拐角處會(huì)略微不精確,這屬于局部影響,也是向模擬引入尖角后的一個(gè)固有問題。
現(xiàn)在,如果我們要處理類似鋁箔這種一個(gè)維度遠(yuǎn)小于其他維度的物體呢?此時(shí),一個(gè)方向上的集膚深度可能會(huì)與厚度相當(dāng),因此電磁場(chǎng)將部分穿透材料。此時(shí)就不再適合使用 IBC,我們將使用過渡邊界條件。
過渡邊界條件
過渡邊界條件 (TBC) 適用于模擬物體的厚度與特征尺寸和曲率相比較小的導(dǎo)電材料層。即使厚度是集膚深度的數(shù)倍,還是可以使用 TBC。
TBC 會(huì)將材料屬性及膜厚度作為輸入項(xiàng),并通過膜厚度及切向阻抗來計(jì)算阻抗。這些可以用于將膜兩側(cè)表面的電流關(guān)聯(lián)起來。也就是說,TBC 會(huì)造成所傳輸電場(chǎng)的下降。
從計(jì)算的角度來看,為了計(jì)算 TBC 兩側(cè)的電場(chǎng),邊界處的自由度數(shù)將增加一倍,如下圖所示。此外,還將計(jì)算通過膜厚度的總損耗。有關(guān)該邊界條件使用的示例,您可以查看分光器教程案例,它利用一個(gè)復(fù)數(shù)值介電常數(shù)模擬了銀薄層。
過渡邊界條件會(huì)計(jì)算邊界兩側(cè)的表面電流。
增加表面粗糙度
截至目前,TBC 和 IBC 都假定表面是完美的。我們一般認(rèn)為平面邊界在幾何上是完美的。彎曲邊界可以在所用有限元網(wǎng)格的精度內(nèi)被解析,即幾何的離散誤差。
與平滑表面相比,粗糙表面會(huì)阻礙電流。
但所有真實(shí)表面都存在一定的粗糙度,而且可能很大。表面的不完美將影響電流的純切向流動(dòng),并會(huì)有效降低表面電導(dǎo)率(如上圖所示)。在 COMSOL 軟件中,我們可以通過向 IBC 和 TBC 條件增加表面粗糙度特征來分析該影響。
對(duì)于 IBC,輸入是表面高度粗糙度的均方根 (RMS)。對(duì)于 TBC,輸入為膜厚度變化的均方根。粗糙度的幅值應(yīng)大于集膚深度,并遠(yuǎn)小于零件的特征尺寸。表面的等效電導(dǎo)率會(huì)隨粗糙度的升高而降低,如 E. Hammerstad 和 O. Jensen 在 “微帶線計(jì)算機(jī)輔助設(shè)計(jì)的精確模型” 論文中的介紹。雪球模型是第二個(gè)粗糙度模型,用到了 P. G. Huray 在“信號(hào)完整性基礎(chǔ)” 中提到的關(guān)系式。
完美電導(dǎo)體邊界條件
我們還應(yīng)該再分析一種理想化的情況 — 完美電導(dǎo)體 (PEC) 邊界條件。對(duì)于無線電和微波領(lǐng)域的許多應(yīng)用而言,金屬邊界處的損耗要遠(yuǎn)小于系統(tǒng)內(nèi)的其他損耗。例如在微波電路中,電介質(zhì)基板處的損耗通常遠(yuǎn)大于任何金屬噴鍍處的損耗。
PEC 邊界是一種無損耗表面;能夠 100% 反射入射波。該邊界條件可以滿足許多模擬需求,可以用在模型開發(fā)的早期階段。有時(shí),查看您的設(shè)備在零材料損耗下的表現(xiàn)也會(huì)很有意思。
此外,您可以將 PEC 邊界條件作為對(duì)稱條件使用,簡(jiǎn)化您的模擬。根據(jù)對(duì)場(chǎng)的預(yù)先判斷,您可以使用 PEC 邊界條件以及其補(bǔ)充,完美磁導(dǎo)體 (PMC) 邊界條件,來使電場(chǎng)強(qiáng)制對(duì)稱。計(jì)算完美導(dǎo)體球的雷達(dá)截面教程案例介紹了如何將 PEC 和 PMC 邊界條件作為對(duì)稱條件使用。
最后,COMSOL Multiphysics 中還包括表面電流、磁場(chǎng)和電場(chǎng)邊界條件。提供這些條件主要是考慮數(shù)學(xué)上的完整性,因?yàn)槲覀冇肋h(yuǎn)也無法事先得知表面上的電流和電場(chǎng)。
小結(jié)
在本篇文章中,我們重點(diǎn)介紹了如何借助阻抗、過渡及完美電導(dǎo)體邊界條件來模擬金屬表面,并說明了每種邊界的應(yīng)用場(chǎng)景。不過,如果您無法使用其中任意一種邊界條件呢?或者您模擬零件的特征尺寸與集膚深度類似?此時(shí),您將不能再使用邊界條件;您需要顯式模擬金屬域,類似于對(duì)其他所有材料的處理。這是該系列的下一個(gè)主題,請(qǐng)繼續(xù)關(guān)注。
-
阻抗
+關(guān)注
關(guān)注
17文章
961瀏覽量
46185 -
導(dǎo)電材料
+關(guān)注
關(guān)注
0文章
60瀏覽量
10975
原文標(biāo)題:模擬電磁波問題中的金屬物體——選擇合適的邊界條件
文章出處:【微信號(hào):COMSOL-China,微信公眾號(hào):COMSOL】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
頻域內(nèi)電磁波仿真所使用多種域和邊界條件
HFSS v9邊界條件和激勵(lì)設(shè)置培訓(xùn)
對(duì)流傳質(zhì)的Neuman-type邊界條件如何編寫?
HFSS的三種吸收邊界條件
LPS25HBT設(shè)計(jì)外殼的邊界條件是什么?
不同電磁邊界設(shè)置的仿真研究
時(shí)變電磁場(chǎng)的邊界條件
基于MARMOUSI的PML邊界條件的研究

壓力邊界條件對(duì)方形腔液力變矩器CFD計(jì)算的影響分析
什么是電磁場(chǎng)的邊界條件
傳導(dǎo)冷卻模塊仿真的邊界條件
對(duì)Fluent邊界條件進(jìn)行簡(jiǎn)易分類
AN50019:MOSFET封裝的熱邊界條件研究





 阻抗、過渡邊界條件和完美電導(dǎo)體邊界條件
阻抗、過渡邊界條件和完美電導(dǎo)體邊界條件










評(píng)論