排序算法大體可分為兩種:
一種是比較排序,時間復雜度O(nlogn) ~ O(n^2),主要有:冒泡排序,選擇排序,插入排序,歸并排序,堆排序,快速排序等。
另一種是非比較排序,時間復雜度可以達到O(n),主要有:計數(shù)排序,基數(shù)排序,桶排序等。
這里我們來探討一下常用的比較排序算法,非比較排序算法將在下一篇文章中介紹。下表給出了常見比較排序算法的性能:
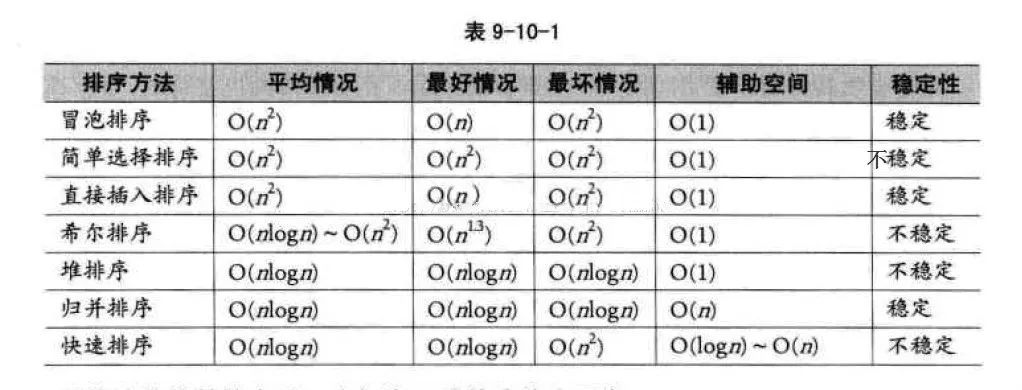
有一點我們很容易忽略的是排序算法的穩(wěn)定性(騰訊校招2016筆試題曾考過)。
排序算法穩(wěn)定性的簡單形式化定義為:如果Ai= Aj,排序前Ai在Aj之前,排序后Ai還在Aj之前,則稱這種排序算法是穩(wěn)定的。通俗地講就是保證排序前后兩個相等的數(shù)的相對順序不變。
對于不穩(wěn)定的排序算法,只要舉出一個實例,即可說明它的不穩(wěn)定性;而對于穩(wěn)定的排序算法,必須對算法進行分析從而得到穩(wěn)定的特性。需要注意的是,排序算法是否為穩(wěn)定的是由具體算法決定的,不穩(wěn)定的算法在某種條件下可以變?yōu)榉€(wěn)定的算法,而穩(wěn)定的算法在某種條件下也可以變?yōu)椴环€(wěn)定的算法。
例如,對于冒泡排序,原本是穩(wěn)定的排序算法,如果將記錄交換的條件改成A[i] >= A[i + 1],則兩個相等的記錄就會交換位置,從而變成不穩(wěn)定的排序算法。
其次,說一下排序算法穩(wěn)定性的好處。排序算法如果是穩(wěn)定的,那么從一個鍵上排序,然后再從另一個鍵上排序,前一個鍵排序的結(jié)果可以為后一個鍵排序所用。基數(shù)排序就是這樣,先按低位排序,逐次按高位排序,低位排序后元素的順序在高位也相同時是不會改變的。
冒泡排序(Bubble Sort)
冒泡排序是一種極其簡單的排序算法,也是我所學的第一個排序算法。它重復地走訪過要排序的元素,依次比較相鄰兩個元素,如果他們的順序錯誤就把他們調(diào)換過來,直到?jīng)]有元素再需要交換,排序完成。這個算法的名字由來是因為越小(或越大)的元素會經(jīng)由交換慢慢“浮”到數(shù)列的頂端。
冒泡排序算法的運作如下:
比較相鄰的元素,如果前一個比后一個大,就把它們兩個調(diào)換位置。
對每一對相鄰元素作同樣的工作,從開始第一對到結(jié)尾的最后一對。這步做完后,最后的元素會是最大的數(shù)。
針對所有的元素重復以上的步驟,除了最后一個。
持續(xù)每次對越來越少的元素重復上面的步驟,直到?jīng)]有任何一對數(shù)字需要比較。
由于它的簡潔,冒泡排序通常被用來對于程序設(shè)計入門的學生介紹算法的概念。冒泡排序的代碼如下:
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- O(n^2)
// 最優(yōu)時間復雜度 ---- 如果能在內(nèi)部循環(huán)第一次運行時,使用一個旗標來表示有無需要交換的可能,可以把最優(yōu)時間復雜度降低到O(n)
// 平均時間復雜度 ---- O(n^2)
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 穩(wěn)定
voidSwap(intA[],inti,intj)
{
inttemp = A[i];
A[i] = A[j];
A[j] = temp;
}
voidBubbleSort(intA[],intn)
{
for(intj = 0;j1;j++) // 每次最大元素就像氣泡一樣"浮"到數(shù)組的最后
{
for(inti = 0;i1 - j;i++)// 依次比較相鄰的兩個元素,使較大的那個向后移
{
if(A[i] > A[i + 1])// 如果條件改成A[i] >= A[i + 1],則變?yōu)椴环€(wěn)定的排序算法
{
Swap(A,i,i + 1);
}
}
}
}
intmain()
{
intA[] = {6,5,3,1,8,7,2,4};// 從小到大冒泡排序
intn = sizeof(A) / sizeof(int);
BubbleSort(A,n);
printf("冒泡排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
上述代碼對序列{ 6, 5, 3, 1, 8, 7, 2, 4 }進行冒泡排序的實現(xiàn)過程如下
使用冒泡排序為一列數(shù)字進行排序的過程如右圖所示:
盡管冒泡排序是最容易了解和實現(xiàn)的排序算法之一,但它對于少數(shù)元素之外的數(shù)列排序是很沒有效率的。
冒泡排序的改進:雞尾酒排序
雞尾酒排序,也叫定向冒泡排序,是冒泡排序的一種改進。此算法與冒泡排序的不同處在于從低到高然后從高到低,而冒泡排序則僅從低到高去比較序列里的每個元素。他可以得到比冒泡排序稍微好一點的效能。
雞尾酒排序的代碼如下:
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- O(n^2)
// 最優(yōu)時間復雜度 ---- 如果序列在一開始已經(jīng)大部分排序過的話,會接近O(n)
// 平均時間復雜度 ---- O(n^2)
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 穩(wěn)定
voidSwap(intA[],inti,intj)
{
inttemp = A[i];
A[i] = A[j];
A[j] = temp;
}
voidCocktailSort(intA[],intn)
{
intleft = 0;// 初始化邊界
intright = n - 1;
while(leftright)
{
for(inti = left;i// 前半輪,將最大元素放到后面
{
if(A[i] > A[i + 1])
{
Swap(A,i,i + 1);
}
}
right--;
for(inti = right;i > left;i--) // 后半輪,將最小元素放到前面
{
if(A[i - 1] > A[i])
{
Swap(A,i - 1,i);
}
}
left++;
}
}
intmain()
{
intA[] = {6,5,3,1,8,7,2,4}; // 從小到大定向冒泡排序
intn = sizeof(A) / sizeof(int);
CocktailSort(A,n);
printf("雞尾酒排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
使用雞尾酒排序為一列數(shù)字進行排序的過程如右圖所示:
以序列(2,3,4,5,1)為例,雞尾酒排序只需要訪問一次序列就可以完成排序,但如果使用冒泡排序則需要四次。但是在亂數(shù)序列的狀態(tài)下,雞尾酒排序與冒泡排序的效率都很差勁。
選擇排序(Selection Sort)
選擇排序也是一種簡單直觀的排序算法。它的工作原理很容易理解:初始時在序列中找到最小(大)元素,放到序列的起始位置作為已排序序列;然后,再從剩余未排序元素中繼續(xù)尋找最小(大)元素,放到已排序序列的末尾。以此類推,直到所有元素均排序完畢。
注意選擇排序與冒泡排序的區(qū)別:冒泡排序通過依次交換相鄰兩個順序不合法的元素位置,從而將當前最小(大)元素放到合適的位置;而選擇排序每遍歷一次都記住了當前最小(大)元素的位置,最后僅需一次交換操作即可將其放到合適的位置。
選擇排序的代碼如下:
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- O(n^2)
// 最優(yōu)時間復雜度 ---- O(n^2)
// 平均時間復雜度 ---- O(n^2)
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 不穩(wěn)定
voidSwap(intA[],inti,intj)
{
inttemp = A[i];
A[i] = A[j];
A[j] = temp;
}
voidSelectionSort(intA[],intn)
{
for(inti = 0;i1;i++) // i為已排序序列的末尾
{
intmin = i;
for(intj = i + 1;j// 未排序序列
{
if(A[j]// 找出未排序序列中的最小值
{
min = j;
}
}
if(min != i)
{
Swap(A,min,i);// 放到已排序序列的末尾,該操作很有可能把穩(wěn)定性打亂,所以選擇排序是不穩(wěn)定的排序算法
}
}
}
intmain()
{
intA[] = {8,5,2,6,9,3,1,4,0,7};// 從小到大選擇排序
intn = sizeof(A) / sizeof(int);
SelectionSort(A,n);
printf("選擇排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
上述代碼對序列{ 8, 5, 2, 6, 9, 3, 1, 4, 0, 7 }進行選擇排序的實現(xiàn)過程如右圖:
使用選擇排序為一列數(shù)字進行排序的宏觀過程:
選擇排序是不穩(wěn)定的排序算法,不穩(wěn)定發(fā)生在最小元素與A[i]交換的時刻。
比如序列:{ 5, 8, 5, 2, 9 },一次選擇的最小元素是2,然后把2和第一個5進行交換,從而改變了兩個元素5的相對次序。
插入排序(Insertion Sort)
插入排序是一種簡單直觀的排序算法。它的工作原理非常類似于我們抓撲克牌
對于未排序數(shù)據(jù)(右手抓到的牌),在已排序序列(左手已經(jīng)排好序的手牌)中從后向前掃描,找到相應(yīng)位置并插入。
插入排序在實現(xiàn)上,通常采用in-place排序(即只需用到O(1)的額外空間的排序),因而在從后向前掃描過程中,需要反復把已排序元素逐步向后挪位,為最新元素提供插入空間。
具體算法描述如下:
從第一個元素開始,該元素可以認為已經(jīng)被排序
取出下一個元素,在已經(jīng)排序的元素序列中從后向前掃描
如果該元素(已排序)大于新元素,將該元素移到下一位置
重復步驟3,直到找到已排序的元素小于或者等于新元素的位置
將新元素插入到該位置后
重復步驟2~5
插入排序的代碼如下:
#include // 分類 ------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- 最壞情況為輸入序列是降序排列的,此時時間復雜度O(n^2)
// 最優(yōu)時間復雜度 ---- 最好情況為輸入序列是升序排列的,此時時間復雜度O(n)
// 平均時間復雜度 ---- O(n^2)
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 穩(wěn)定
voidInsertionSort(intA[],intn)
{
for(inti = 1;i// 類似抓撲克牌排序
{
intget = A[i]; // 右手抓到一張撲克牌
intj = i - 1;// 拿在左手上的牌總是排序好的
while(j >= 0 && A[j] > get)// 將抓到的牌與手牌從右向左進行比較
{
A[j + 1] = A[j];// 如果該手牌比抓到的牌大,就將其右移
j--;
}
A[j + 1] = get;// 直到該手牌比抓到的牌小(或二者相等),將抓到的牌插入到該手牌右邊(相等元素的相對次序未變,所以插入排序是穩(wěn)定的)
}
}
intmain()
{
intA[] = {6,5,3,1,8,7,2,4};// 從小到大插入排序
intn = sizeof(A) / sizeof(int);
InsertionSort(A,n);
printf("插入排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
上述代碼對序列{ 6, 5, 3, 1, 8, 7, 2, 4 }進行插入排序的實現(xiàn)過程如下
使用插入排序為一列數(shù)字進行排序的宏觀過程:
插入排序不適合對于數(shù)據(jù)量比較大的排序應(yīng)用。但是,如果需要排序的數(shù)據(jù)量很小,比如量級小于千,那么插入排序還是一個不錯的選擇。 插入排序在工業(yè)級庫中也有著廣泛的應(yīng)用,在STL的sort算法和stdlib的qsort算法中,都將插入排序作為快速排序的補充,用于少量元素的排序(通常為8個或以下)。
插入排序的改進:二分插入排序
對于插入排序,如果比較操作的代價比交換操作大的話,可以采用二分查找法來減少比較操作的次數(shù),我們稱為二分插入排序,代碼如下:
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- O(n^2)
// 最優(yōu)時間復雜度 ---- O(nlogn)
// 平均時間復雜度 ---- O(n^2)
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 穩(wěn)定
voidInsertionSortDichotomy(intA[],intn)
{
for(inti = 1;i)
{
intget = A[i];// 右手抓到一張撲克牌
intleft = 0;// 拿在左手上的牌總是排序好的,所以可以用二分法
intright = i - 1;// 手牌左右邊界進行初始化
while(left// 采用二分法定位新牌的位置
{
intmid = (left + right) / 2;
if(A[mid] > get)
right = mid - 1;
else
left = mid + 1;
}
for(intj = i - 1;j >= left;j--)// 將欲插入新牌位置右邊的牌整體向右移動一個單位
{
A[j + 1] = A[j];
}
A[left] = get;// 將抓到的牌插入手牌
}
}
intmain()
{
intA[] = {5,2,9,4,7,6,1,3,8};// 從小到大二分插入排序
intn = sizeof(A) / sizeof(int);
InsertionSortDichotomy(A,n);
printf("二分插入排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
當n較大時,二分插入排序的比較次數(shù)比直接插入排序的最差情況好得多,但比直接插入排序的最好情況要差,所當以元素初始序列已經(jīng)接近升序時,直接插入排序比二分插入排序比較次數(shù)少。二分插入排序元素移動次數(shù)與直接插入排序相同,依賴于元素初始序列。
插入排序的更高效改進:希爾排序(Shell Sort)
希爾排序,也叫遞減增量排序,是插入排序的一種更高效的改進版本。希爾排序是不穩(wěn)定的排序算法。
希爾排序是基于插入排序的以下兩點性質(zhì)而提出改進方法的:
插入排序在對幾乎已經(jīng)排好序的數(shù)據(jù)操作時,效率高,即可以達到線性排序的效率
但插入排序一般來說是低效的,因為插入排序每次只能將數(shù)據(jù)移動一位
希爾排序通過將比較的全部元素分為幾個區(qū)域來提升插入排序的性能。這樣可以讓一個元素可以一次性地朝最終位置前進一大步。然后算法再取越來越小的步長進行排序,算法的最后一步就是普通的插入排序,但是到了這步,需排序的數(shù)據(jù)幾乎是已排好的了(此時插入排序較快)。假設(shè)有一個很小的數(shù)據(jù)在一個已按升序排好序的數(shù)組的末端。如果用復雜度為O(n^2)的排序(冒泡排序或直接插入排序),可能會進行n次的比較和交換才能將該數(shù)據(jù)移至正確位置。而希爾排序會用較大的步長移動數(shù)據(jù),所以小數(shù)據(jù)只需進行少數(shù)比較和交換即可到正確位置。
希爾排序的代碼如下:
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- 根據(jù)步長序列的不同而不同。已知最好的為O(n(logn)^2)
// 最優(yōu)時間復雜度 ---- O(n)
// 平均時間復雜度 ---- 根據(jù)步長序列的不同而不同。
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 不穩(wěn)定
voidShellSort(intA[],intn)
{
inth = 0;
while(h// 生成初始增量
{
h = 3 * h + 1;
}
while(h >= 1)
{
for(inti = h;i)
{
intj = i - h;
intget = A[i];
while(j >= 0 && A[j] > get)
{
A[j + h] = A[j];
j = j - h;
}
A[j + h] = get;
}
h = (h - 1) / 3;// 遞減增量
}
}
intmain()
{
intA[] = {5,2,9,4,7,6,1,3,8};// 從小到大希爾排序
intn = sizeof(A) / sizeof(int);
ShellSort(A,n);
printf("希爾排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
以23, 10, 4, 1的步長序列進行希爾排序:
希爾排序是不穩(wěn)定的排序算法,雖然一次插入排序是穩(wěn)定的,不會改變相同元素的相對順序,但在不同的插入排序過程中,相同的元素可能在各自的插入排序中移動,最后其穩(wěn)定性就會被打亂。
比如序列:{3, 5,10,8, 7, 2, 8, 1, 20, 6 },h=2時分成兩個子序列{3, 10, 7, 8, 20 } 和{5, 8, 2, 1, 6 } ,未排序之前第二個子序列中的8在前面,現(xiàn)在對兩個子序列進行插入排序,得到{3,7,8,10, 20 } 和 {1,2,5,6,8} ,即{3, 1,7,2, 8, 5,10, 6, 20, 8 } ,兩個8的相對次序發(fā)生了改變。
歸并排序(Merge Sort)
歸并排序是創(chuàng)建在歸并操作上的一種有效的排序算法,效率為O(nlogn),1945年由馮·諾伊曼首次提出。
歸并排序的實現(xiàn)分為遞歸實現(xiàn)與非遞歸(迭代)實現(xiàn)。遞歸實現(xiàn)的歸并排序是算法設(shè)計中分治策略的典型應(yīng)用,我們將一個大問題分割成小問題分別解決,然后用所有小問題的答案來解決整個大問題。非遞歸(迭代)實現(xiàn)的歸并排序首先進行是兩兩歸并,然后四四歸并,然后是八八歸并,一直下去直到歸并了整個數(shù)組。
歸并排序算法主要依賴歸并(Merge)操作。歸并操作指的是將兩個已經(jīng)排序的序列合并成一個序列的操作,歸并操作步驟如下:
申請空間,使其大小為兩個已經(jīng)排序序列之和,該空間用來存放合并后的序列
設(shè)定兩個指針,最初位置分別為兩個已經(jīng)排序序列的起始位置
比較兩個指針所指向的元素,選擇相對小的元素放入到合并空間,并移動指針到下一位置
重復步驟3直到某一指針到達序列尾
將另一序列剩下的所有元素直接復制到合并序列尾
歸并排序的代碼如下:
#include
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- O(nlogn)
// 最優(yōu)時間復雜度 ---- O(nlogn)
// 平均時間復雜度 ---- O(nlogn)
// 所需輔助空間 ------ O(n)
// 穩(wěn)定性 ------------ 穩(wěn)定
voidMerge(intA[],intleft,intmid,intright)// 合并兩個已排好序的數(shù)組A[left...mid]和A[mid+1...right]
{
intlen = right - left + 1;
int *temp = newint[len]; // 輔助空間O(n)
intindex = 0;
inti = left; // 前一數(shù)組的起始元素
intj = mid + 1;// 后一數(shù)組的起始元素
while(iright)
{
temp[index++] = A[i]// 帶等號保證歸并排序的穩(wěn)定性
}
while(imid)
{
temp[index++] = A[i++];
}
while(jright)
{
temp[index++] = A[j++];
}
for(intk = 0;k)
{
A[left++] = temp[k];
}
}
voidMergeSortRecursion(intA[],intleft,intright)// 遞歸實現(xiàn)的歸并排序(自頂向下)
{
if(left == right)// 當待排序的序列長度為1時,遞歸開始回溯,進行merge操作
return;
intmid = (left + right) / 2;
MergeSortRecursion(A,left,mid);
MergeSortRecursion(A,mid + 1,right);
Merge(A,left,mid,right);
}
voidMergeSortIteration(intA[],intlen)// 非遞歸(迭代)實現(xiàn)的歸并排序(自底向上)
{
intleft,mid,right;// 子數(shù)組索引,前一個為A[left...mid],后一個子數(shù)組為A[mid+1...right]
for(inti = 1;i2)// 子數(shù)組的大小i初始為1,每輪翻倍
{
left = 0;
while(left + i// 后一個子數(shù)組存在(需要歸并)
{
mid = left + i - 1;
right = mid + i1;// 后一個子數(shù)組大小可能不夠
Merge(A,left,mid,right);
left = right + 1; // 前一個子數(shù)組索引向后移動
}
}
}
intmain()
{
intA1[] = {6,5,3,1,8,7,2,4};// 從小到大歸并排序
intA2[] = {6,5,3,1,8,7,2,4};
intn1 = sizeof(A1) / sizeof(int);
intn2 = sizeof(A2) / sizeof(int);
MergeSortRecursion(A1,0,n1 - 1);// 遞歸實現(xiàn)
MergeSortIteration(A2,n2); // 非遞歸實現(xiàn)
printf("遞歸實現(xiàn)的歸并排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A1[i]);
}
printf("n");
printf("非遞歸實現(xiàn)的歸并排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A2[i]);
}
printf("n");
return0;
}
上述代碼對序列{ 6, 5, 3, 1, 8, 7, 2, 4 }進行歸并排序的實例如下
使用歸并排序為一列數(shù)字進行排序的宏觀過程:
歸并排序除了可以對數(shù)組進行排序,還可以高效的求出數(shù)組小和(即單調(diào)和)以及數(shù)組中的逆序?qū)Γ斠娺@篇博文。
堆排序(Heap Sort)
堆排序是指利用堆這種數(shù)據(jù)結(jié)構(gòu)所設(shè)計的一種選擇排序算法。堆是一種近似完全二叉樹的結(jié)構(gòu)(通常堆是通過一維數(shù)組來實現(xiàn)的),并滿足性質(zhì):以最大堆(也叫大根堆、大頂堆)為例,其中父結(jié)點的值總是大于它的孩子節(jié)點。
我們可以很容易的定義堆排序的過程:
由輸入的無序數(shù)組構(gòu)造一個最大堆,作為初始的無序區(qū)
把堆頂元素(最大值)和堆尾元素互換
把堆(無序區(qū))的尺寸縮小1,并調(diào)用heapify(A, 0)從新的堆頂元素開始進行堆調(diào)整
重復步驟2,直到堆的尺寸為1
堆排序的代碼如下:
#include // 分類 -------------- 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) ---------- 數(shù)組
// 最差時間復雜度 ---- O(nlogn)
// 最優(yōu)時間復雜度 ---- O(nlogn)
// 平均時間復雜度 ---- O(nlogn)
// 所需輔助空間 ------ O(1)
// 穩(wěn)定性 ------------ 不穩(wěn)定
voidSwap(intA[],inti,intj)
{
inttemp = A[i];
A[i] = A[j];
A[j] = temp;
}
voidHeapify(intA[],inti,intsize)// 從A[i]向下進行堆調(diào)整
{
intleft_child = 2 * i + 1; // 左孩子索引
intright_child = 2 * i + 2;// 右孩子索引
intmax = i;// 選出當前結(jié)點與其左右孩子三者之中的最大值
if(left_childA[max])
max = left_child;
if(right_childA[max])
max = right_child;
if(max != i)
{
Swap(A,i,max);// 把當前結(jié)點和它的最大(直接)子節(jié)點進行交換
Heapify(A,max,size);// 遞歸調(diào)用,繼續(xù)從當前結(jié)點向下進行堆調(diào)整
}
}
intBuildHeap(intA[],intn) // 建堆,時間復雜度O(n)
{
intheap_size = n;
for(inti = heap_size / 2 - 1;i >= 0;i--)// 從每一個非葉結(jié)點開始向下進行堆調(diào)整
Heapify(A,i,heap_size);
returnheap_size;
}
voidHeapSort(intA[],intn)
{
intheap_size = BuildHeap(A,n);// 建立一個最大堆
while(heap_size > 1)// 堆(無序區(qū))元素個數(shù)大于1,未完成排序
{
// 將堆頂元素與堆的最后一個元素互換,并從堆中去掉最后一個元素
// 此處交換操作很有可能把后面元素的穩(wěn)定性打亂,所以堆排序是不穩(wěn)定的排序算法
Swap(A,0, --heap_size);
Heapify(A,0,heap_size); // 從新的堆頂元素開始向下進行堆調(diào)整,時間復雜度O(logn)
}
}
intmain()
{
intA[] = {5,2,9,4,7,6,1,3,8};// 從小到大堆排序
intn = sizeof(A) / sizeof(int);
HeapSort(A,n);
printf("堆排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
堆排序算法的演示:
動畫中在排序過程之前簡單的表現(xiàn)了創(chuàng)建堆的過程以及堆的邏輯結(jié)構(gòu)。
堆排序是不穩(wěn)定的排序算法,不穩(wěn)定發(fā)生在堆頂元素與A[i]交換的時刻。
比如序列:{ 9, 5, 7,5 },堆頂元素是9,堆排序下一步將9和第二個5進行交換,得到序列{5, 5, 7,9},再進行堆調(diào)整得到{7, 5,5,9},重復之前的操作最后得到{ 5,5, 7,9}從而改變了兩個5的相對次序。
快速排序(Quick Sort)
快速排序是由東尼·霍爾所發(fā)展的一種排序算法。在平均狀況下,排序n個元素要O(nlogn)次比較。在最壞狀況下則需要O(n^2)次比較,但這種狀況并不常見。事實上,快速排序通常明顯比其他O(nlogn)算法更快,因為它的內(nèi)部循環(huán)可以在大部分的架構(gòu)上很有效率地被實現(xiàn)出來。
快速排序使用分治策略(Divide and Conquer)來把一個序列分為兩個子序列。步驟為:
從序列中挑出一個元素,作為”基準”(pivot).
把所有比基準值小的元素放在基準前面,所有比基準值大的元素放在基準的后面(相同的數(shù)可以到任一邊),這個稱為分區(qū)(partition)操作。
對每個分區(qū)遞歸地進行步驟1~2,遞歸的結(jié)束條件是序列的大小是0或1,這時整體已經(jīng)被排好序了。
快速排序的代碼如下:
#include // 分類 ------------ 內(nèi)部比較排序
// 數(shù)據(jù)結(jié)構(gòu) --------- 數(shù)組
// 最差時間復雜度 ---- 每次選取的基準都是最大(或最小)的元素,導致每次只劃分出了一個分區(qū),需要進行n-1次劃分才能結(jié)束遞歸,時間復雜度為O(n^2)
// 最優(yōu)時間復雜度 ---- 每次選取的基準都是中位數(shù),這樣每次都均勻的劃分出兩個分區(qū),只需要logn次劃分就能結(jié)束遞歸,時間復雜度為O(nlogn)
// 平均時間復雜度 ---- O(nlogn)
// 所需輔助空間 ------ 主要是遞歸造成的棧空間的使用(用來保存left和right等局部變量),取決于遞歸樹的深度,一般為O(logn),最差為O(n)
// 穩(wěn)定性 ---------- 不穩(wěn)定
voidSwap(intA[],inti,intj)
{
inttemp = A[i];
A[i] = A[j];
A[j] = temp;
}
intPartition(intA[],intleft,intright)// 劃分函數(shù)
{
intpivot = A[right]; // 這里每次都選擇最后一個元素作為基準
inttail = left - 1;// tail為小于基準的子數(shù)組最后一個元素的索引
for(inti = left;i// 遍歷基準以外的其他元素
{
if(A[i]// 把小于等于基準的元素放到前一個子數(shù)組末尾
{
Swap(A, ++tail,i);
}
}
Swap(A,tail + 1,right); // 最后把基準放到前一個子數(shù)組的后邊,剩下的子數(shù)組既是大于基準的子數(shù)組
// 該操作很有可能把后面元素的穩(wěn)定性打亂,所以快速排序是不穩(wěn)定的排序算法
returntail + 1;// 返回基準的索引
}
voidQuickSort(intA[],intleft,intright)
{
if(left >= right)
return;
intpivot_index = Partition(A,left,right);// 基準的索引
QuickSort(A,left,pivot_index - 1);
QuickSort(A,pivot_index + 1,right);
}
intmain()
{
intA[] = {5,2,9,4,7,6,1,3,8};// 從小到大快速排序
intn = sizeof(A) / sizeof(int);
QuickSort(A,0,n - 1);
printf("快速排序結(jié)果:");
for(inti = 0;i)
{
printf("%d ",A[i]);
}
printf("n");
return0;
}
使用快速排序法對一列數(shù)字進行排序的過程:
快速排序是不穩(wěn)定的排序算法,不穩(wěn)定發(fā)生在基準元素與A[tail+1]交換的時刻。
比如序列:{ 1, 3, 4, 2, 8, 9, 8, 7, 5 },基準元素是5,一次劃分操作后5要和第一個8進行交換,從而改變了兩個元素8的相對次序。
Java系統(tǒng)提供的Arrays.sort函數(shù)。對于基礎(chǔ)類型,底層使用快速排序。對于非基礎(chǔ)類型,底層使用歸并排序。請問是為什么?
答:這是考慮到排序算法的穩(wěn)定性。對于基礎(chǔ)類型,相同值是無差別的,排序前后相同值的相對位置并不重要,所以選擇更為高效的快速排序,盡管它是不穩(wěn)定的排序算法;而對于非基礎(chǔ)類型,排序前后相等實例的相對位置不宜改變,所以選擇穩(wěn)定的歸并排序。
-
排序算法
+關(guān)注
關(guān)注
0文章
53瀏覽量
10088
發(fā)布評論請先 登錄
相關(guān)推薦
嵌入式stm32實用的排序算法 - 交換排序
基于C語言的幾種排序算法的分析
基于Hadoop的幾種排序算法研究

經(jīng)典排序算法和JS實現(xiàn)案例分析
常用的非比較排序算法:計數(shù)排序,基數(shù)排序,桶排序的詳細資料概述
解析數(shù)據(jù)結(jié)構(gòu)的常用七大排序算法
熟練掌握常用的排序算法





 常用排序算法分析
常用排序算法分析











評論