一、簡(jiǎn)介
隱含狄利克雷分布(Latent Dirichlet Allocation,簡(jiǎn)稱(chēng)LDA)是由 David M. Blei、Andrew Y. Ng、Michael I. Jordan 在2003年提出的,是一種詞袋模型,它認(rèn)為文檔是一組詞構(gòu)成的集合,詞與詞之間是無(wú)序的。一篇文檔可以包含多個(gè)主題,文檔中的每個(gè)詞都是由某個(gè)主題生成的,LDA給出文檔屬于每個(gè)主題的概率分布,同時(shí)給出每個(gè)主題上詞的概率分布。LDA是一種無(wú)監(jiān)督學(xué)習(xí),在文本主題識(shí)別、文本分類(lèi)、文本相似度計(jì)算和文章相似推薦等方面都有應(yīng)用。
本文將從貝葉公式、Gamma函數(shù)、二項(xiàng)分布、Beta分布、多項(xiàng)式分布、Dirichlet分布、共軛先驗(yàn)分布、馬氏鏈及其平穩(wěn)分布、MCMC、Gibbs Sampling、EM算法、Unigram Model、貝葉斯Unigram Model、PLSA、LDA 幾方面介紹LDA模型,需要讀者具備一定的概率論和微積分知識(shí)。
二、基礎(chǔ)知識(shí)
▌1.1 貝葉公式
貝葉斯學(xué)派的最基本的觀點(diǎn)是:任一個(gè)未知量θ都可看作一個(gè)隨機(jī)變量,應(yīng)該用一個(gè)概率分布去描述對(duì)θ的未知狀況,這個(gè)概率分布是在抽樣前就有關(guān)于θ的先驗(yàn)信息的概率陳述,這個(gè)概率分布被稱(chēng)為先驗(yàn)分布。
從貝葉斯觀點(diǎn)看,樣本 的產(chǎn)生要分兩步進(jìn)行,首先設(shè)想從先驗(yàn)分布 p(θ) 產(chǎn)生一個(gè)樣本?θ',這一步是“老天爺”做的,人們是看不到的,故用“設(shè)想”二字。第二步是從總體分布?p(X|θ')?產(chǎn)生一個(gè)樣本
的產(chǎn)生要分兩步進(jìn)行,首先設(shè)想從先驗(yàn)分布 p(θ) 產(chǎn)生一個(gè)樣本?θ',這一步是“老天爺”做的,人們是看不到的,故用“設(shè)想”二字。第二步是從總體分布?p(X|θ')?產(chǎn)生一個(gè)樣本 ,這個(gè)樣本是具體的,人們能看得到的,此樣本 X 發(fā)生的概率是與如下聯(lián)合密度函數(shù)成正比。
,這個(gè)樣本是具體的,人們能看得到的,此樣本 X 發(fā)生的概率是與如下聯(lián)合密度函數(shù)成正比。

這個(gè)聯(lián)合密度函數(shù)是綜合了總體信息和樣本信息,常稱(chēng)為似然函數(shù),記為 L(θ')。
由于θ'是設(shè)想出來(lái)的,它仍然是未知的,它是按先驗(yàn)分布p(θ)產(chǎn)生的,要把先驗(yàn)信息進(jìn)行綜合,不能只考慮θ',而應(yīng)對(duì)θ的一切可能加以考慮,故要用p(θ)參與進(jìn)一步綜合,所以樣本 X 和參數(shù)θ的聯(lián)合分布(三種可用的信息都綜合進(jìn)去了):

我們的任務(wù)是要對(duì)未知數(shù)θ 作出統(tǒng)計(jì)推斷,在沒(méi)有樣本信息時(shí),人們只能根據(jù)先驗(yàn)分布對(duì)θ 作出推斷。在有樣本觀察值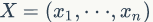 之后,我們應(yīng)該依據(jù)?p(X,θ)?對(duì)?θ 作出推斷,為此我們把?p(X,θ)?作如下分解:
之后,我們應(yīng)該依據(jù)?p(X,θ)?對(duì)?θ 作出推斷,為此我們把?p(X,θ)?作如下分解:

其中p(X)是X 的邊緣密度函數(shù)。

它與θ 無(wú)關(guān),p(X) 中不含θ 的任何信息。因此能用來(lái)對(duì)θ 作出推斷的僅是條件分布 p(θ|X):

這就是貝葉斯公式的密度函數(shù)形式,在樣本 X 給定下,θ 的條件分布被稱(chēng)為θ 的后驗(yàn)分布。它是集中了總體、樣本和先驗(yàn)等三種信息中有關(guān)θ 的一切信息,而又是排除一切與θ無(wú)關(guān)的信息之后得到的結(jié)果,故基于后驗(yàn)分布p(θ|X) 對(duì)θ 進(jìn)行統(tǒng)計(jì)推斷是更合理的。
一般說(shuō)來(lái),先驗(yàn)分布p(θ) 是反映人們?cè)诔闃忧皩?duì)θ 的認(rèn)識(shí),后驗(yàn)分布p(θ|X) 是反映人們?cè)诔闃雍髮?duì)θ 的認(rèn)識(shí),之間的差異是由于樣本的出現(xiàn)后人們對(duì)θ 認(rèn)識(shí)的一種調(diào)整,所以后驗(yàn)分布p(θ|X) 可以看作是人們用總體信息和樣本信息(抽樣信息)對(duì)先驗(yàn)分布p(θ) 作調(diào)整的結(jié)果。下面我們介紹三種估計(jì)方法:
1. 最大似然估計(jì)(ML)
最大似然估計(jì)是找到參數(shù)θ 使得樣本 X 的聯(lián)合概率最大,并不會(huì)考慮先驗(yàn)知識(shí),頻率學(xué)派和貝葉斯學(xué)派都承認(rèn)似然函數(shù),頻率學(xué)派認(rèn)為參數(shù)θ 是客觀存在的,只是未知。求參數(shù)θ 使似然函數(shù)最大,ML估計(jì)問(wèn)題可以用下面公式表示:

通常可以令導(dǎo)數(shù)為 0 求得θ 的值。ML估計(jì)不會(huì)把先驗(yàn)知識(shí)考慮進(jìn)去,很容易出現(xiàn)過(guò)擬合的現(xiàn)象。我們舉個(gè)例子,拋一枚硬幣,假設(shè)正面向上的概率為 p,拋了 N 次,正面出現(xiàn) 次,反面出現(xiàn)
次,反面出現(xiàn) 次,c=1?表示正面,c=0? 表示反面,我們用 ML 估計(jì):
次,c=1?表示正面,c=0? 表示反面,我們用 ML 估計(jì):
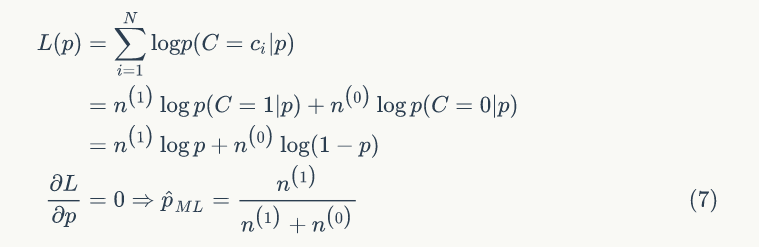
如果 ?,?
?,? ,則
,則 ?,似乎比我們認(rèn)知的 0.5 高了很多。
?,似乎比我們認(rèn)知的 0.5 高了很多。
2. 最大后驗(yàn)估計(jì)(MAP)
MAP 是為了解決 ML 缺少先驗(yàn)知識(shí)的缺點(diǎn),剛好公式 (5) 后驗(yàn)概率集中了樣本信息和先驗(yàn)信息,所以 MAP 估計(jì)問(wèn)題可以用下面公式表示:

MAP 不僅希望似然函數(shù)最大,還希望自己出現(xiàn)的先驗(yàn)概率也最大,加入先驗(yàn)概率,起到正則化的作用,如果θ 服從高斯分布,相當(dāng)于加一個(gè) L2 范數(shù)正則化,如果θ 服從拉普拉斯分布,相當(dāng)于加一個(gè) L1 范數(shù)正則化。我們繼續(xù)前面拋硬幣的例子,大部分人認(rèn)為應(yīng)該等于0.5,那么還有少數(shù)人認(rèn)為 p 取其他值,我們認(rèn)為 p 的取值服從 Beta 分布。

我們?nèi)?α=5,β=5,即 p 以最大的概率取0.5,得到 。
。
3. 貝葉斯估計(jì)
前面介紹的 ML 和 MAP 屬于點(diǎn)估計(jì),貝葉斯估計(jì)不再把參數(shù)θ 看成一個(gè)未知的確定值,而是看成未知的隨機(jī)變量,利用貝葉斯定理結(jié)合新的樣本信息和參數(shù)θ 的先驗(yàn)分布,來(lái)得到θ 的新的概率分布(后驗(yàn)分布)。貝葉斯估計(jì)的本質(zhì)是通過(guò)貝葉斯決策得到參數(shù)θ 的最優(yōu)估計(jì) ,使得貝葉斯期望損失最小。貝葉斯期望損失為:
,使得貝葉斯期望損失最小。貝葉斯期望損失為:

 是損失函數(shù),我們希望
是損失函數(shù),我們希望 ?最小。如果?
?最小。如果? ,則:
,則:

所以貝葉斯估計(jì)值為在樣本 X 條件下θ 的期望值,貝葉斯估計(jì)的步驟為:
確定參數(shù)θ 的先驗(yàn)分布 P(θ)
利用貝葉斯公式,求θ的后驗(yàn)分布:

求出貝葉斯的估計(jì)值:

我們繼續(xù)前面的拋硬幣的例子,后驗(yàn)概率:

其中 ,所以可以得:
,所以可以得:

▌1.2 Gamma函數(shù)

通過(guò)分部積分的方法,可以得到一個(gè)遞歸性質(zhì)。

 函數(shù)可以當(dāng)成是階乘在實(shí)數(shù)集上的延拓,
函數(shù)可以當(dāng)成是階乘在實(shí)數(shù)集上的延拓, 。
。
▌1.3 二項(xiàng)分布
在概率論中,試驗(yàn) E 只有兩個(gè)可能結(jié)果: A 及 ,則稱(chēng)E 為伯努利(Bernoulli)試驗(yàn)。設(shè) p(A)=p,則
,則稱(chēng)E 為伯努利(Bernoulli)試驗(yàn)。設(shè) p(A)=p,則 。將 E 獨(dú)立重復(fù)地進(jìn)行 n 次,則稱(chēng)這一串重復(fù)的獨(dú)立試驗(yàn)為 n 重伯努利試驗(yàn),這里重復(fù)是指在每次試驗(yàn)中?p(A)=p?保持不變,獨(dú)立是指各次試驗(yàn)的結(jié)果互不影響。以 X 表示 n 重伯努利試驗(yàn)中事件 A 發(fā)生的次數(shù),稱(chēng)隨機(jī)變量 X 服從參數(shù)為 n,p 的二項(xiàng)分布,記為X~B(n,p) 。
。將 E 獨(dú)立重復(fù)地進(jìn)行 n 次,則稱(chēng)這一串重復(fù)的獨(dú)立試驗(yàn)為 n 重伯努利試驗(yàn),這里重復(fù)是指在每次試驗(yàn)中?p(A)=p?保持不變,獨(dú)立是指各次試驗(yàn)的結(jié)果互不影響。以 X 表示 n 重伯努利試驗(yàn)中事件 A 發(fā)生的次數(shù),稱(chēng)隨機(jī)變量 X 服從參數(shù)為 n,p 的二項(xiàng)分布,記為X~B(n,p) 。

▌1.4 Beta分布
Beta分布是指一組定義在(0,1)區(qū)間的連續(xù)概率分布,其概率密度函數(shù)是:

1)

證明:

令 t=x+y,當(dāng) y=0,t=x ; y=∞,t=∞,可得:

令 x=μt,可得:

2)期望
證明:

▌1.5 多項(xiàng)式分布
多項(xiàng)式分布是二項(xiàng)式分布的推廣,二項(xiàng)式分布做 n 次伯努利試驗(yàn),規(guī)定每次試驗(yàn)的結(jié)果只有兩個(gè),而多項(xiàng)式分布在 N 次獨(dú)立試驗(yàn)中結(jié)果有 K 種,且每種結(jié)果都有一個(gè)確定的概率 p,仍骰子是典型的多項(xiàng)式分布。

其中

▌1.6 Dirichlet分布
Dirichlet 分布是 Beta 分布在高維度上的推廣,概率密度函數(shù)是:

▌1.7 共軛先驗(yàn)分布
在貝葉斯中,如果后驗(yàn)分布與先驗(yàn)分布屬于同類(lèi)分布,則先驗(yàn)分布與后驗(yàn)分布被稱(chēng)為共軛分布,而先驗(yàn)分布被稱(chēng)為似然函數(shù)的共軛先驗(yàn)。
1.Beta-Binomial共軛
1)先驗(yàn)分布

2)二項(xiàng)式似然函數(shù)

3)后驗(yàn)分布

即可以表達(dá)為

取一個(gè)特殊情況理解

Beta(p|1,1)恰好是均勻分布 uniform(0,1) ,假設(shè)有一個(gè)不均勻的硬幣拋出正面的概率為 p,拋出 n 次后出現(xiàn)正面和反面的次數(shù)分別是 n1 和 n2 ,開(kāi)始我們對(duì)硬幣不均勻性一無(wú)所知,所以應(yīng)該假設(shè) p~uniform(0,1) ,當(dāng)有了試驗(yàn)樣本,我們加入樣本信息對(duì) p 的分布進(jìn)行修正, p 的分布由均勻分布變?yōu)锽eta 分布。
2.Dirichlet-Multinomial共軛
1)先驗(yàn)分布

2)多項(xiàng)分布似然函數(shù)

3)后驗(yàn)分布

即可以表達(dá)為

▌1.8 馬氏鏈及其平穩(wěn)分布
馬氏鏈的數(shù)學(xué)定義很簡(jiǎn)單,狀態(tài)轉(zhuǎn)移的概率只依賴(lài)于前一個(gè)狀態(tài)。

看一個(gè)馬氏鏈的具體例子,馬氏鏈表示股市模型,共有三種狀態(tài):牛市(Bull market)、熊市(Bear market)、橫盤(pán)(Stagnant market),每一個(gè)轉(zhuǎn)態(tài)都以一定的概率轉(zhuǎn)化到下一個(gè)狀態(tài),如圖1.1所示。

圖1.1
這個(gè)概率轉(zhuǎn)化圖可以以矩陣的形式表示,如果我們定義矩陣 P 某一位置 (i,j) 的值為P(j|i),表示從狀態(tài) i 轉(zhuǎn)化到狀態(tài) j的概率,這樣我們可以得到馬爾科夫鏈模型的狀態(tài)轉(zhuǎn)移矩陣為:

假設(shè)初始概率分布為

從第60輪開(kāi)始 的值保持不變,為[0.625? 0.3125? 0.0625]? 。我們更改初始概率,
的值保持不變,為[0.625? 0.3125? 0.0625]? 。我們更改初始概率, ,從55輪開(kāi)始
,從55輪開(kāi)始
的值保持不變,為[0.625 0.3125 0.0625]。兩次給定不同的初始概率分布,最終都收斂到概率分布π=[0.625 0.3125 0.0625] ,也就是說(shuō)收斂的行為和初始概率分布π0 無(wú)關(guān),這個(gè)收斂的行為主要是由概率轉(zhuǎn)移矩陣 P 決定的,可以計(jì)算下 。
。

當(dāng) n 足夠大的時(shí)候, 矩陣的每一行都是穩(wěn)定地收斂到?π=[0.625? 0.3125? 0.0625]? 這個(gè)概率分布。這個(gè)收斂現(xiàn)象并不是這個(gè)馬氏鏈獨(dú)有的,而是絕大多數(shù)馬氏鏈獨(dú)有的。關(guān)于馬氏鏈的收斂有如下定理:
矩陣的每一行都是穩(wěn)定地收斂到?π=[0.625? 0.3125? 0.0625]? 這個(gè)概率分布。這個(gè)收斂現(xiàn)象并不是這個(gè)馬氏鏈獨(dú)有的,而是絕大多數(shù)馬氏鏈獨(dú)有的。關(guān)于馬氏鏈的收斂有如下定理:
定理1.1如果一個(gè)非周期馬氏鏈具有轉(zhuǎn)移概率矩陣 P,且它的任何兩個(gè)狀態(tài)是連通的,那么 存在且與 i 無(wú)關(guān),我們有:?
存在且與 i 無(wú)關(guān),我們有:?

關(guān)于上述定理,給出幾點(diǎn)解釋?zhuān)?/p>
1) 馬氏鏈的狀態(tài)數(shù)可以是有限的,也可以是無(wú)限的,因此可以用于連續(xù)概率分布和離散概率分布。
2) 非周期馬氏鏈:馬氏鏈的狀態(tài)轉(zhuǎn)化不是循環(huán)的,如果是循環(huán)的則永遠(yuǎn)不會(huì)收斂,我們遇到的一般都是非周期馬氏鏈。對(duì)于任意某一狀態(tài)i,d 為集合 的最大公約數(shù),如果 d=1,則該狀態(tài)為非周期。?
的最大公約數(shù),如果 d=1,則該狀態(tài)為非周期。?
3) 任何兩個(gè)狀態(tài)是連通的:從任意一個(gè)狀態(tài)可以通過(guò)有限步到達(dá)其他的任意狀態(tài),不會(huì)出現(xiàn)條件概率一直為0導(dǎo)致不可達(dá)的情況。
4)π稱(chēng)為馬氏鏈的平穩(wěn)分布。
如果從一個(gè)具體的初始狀態(tài) x0 開(kāi)始,沿著馬氏鏈按照概率轉(zhuǎn)移矩陣做跳轉(zhuǎn),那么可以得到一個(gè)轉(zhuǎn)移序列 ,由于馬氏鏈的收斂行為,
,由于馬氏鏈的收斂行為, 都將是平穩(wěn)分布?π(x)?的樣本。
都將是平穩(wěn)分布?π(x)?的樣本。
▌1.9 MCMC
1. 接受-拒絕采樣
對(duì)于不常見(jiàn)的概率分布π(x) 樣本,使用接受-拒絕采樣對(duì)可采樣的分布 q(x) 進(jìn)行采樣得到,如圖1.2所示,采樣得到 Mq(x) 的一個(gè)樣本 x0,從均勻分布 (0,Mq(x0))中采樣得到一個(gè)值μ0 ,如果μ0 落在圖中灰色區(qū)域則拒絕這次采樣,否則接受樣本 x0,重復(fù)上面過(guò)程得到 n 個(gè)接受的樣本,則這些樣本服從π(x)分布,具體過(guò)程見(jiàn)算法1.1。

圖1.2

下面我們來(lái)證明下接受-拒絕方法采樣得到的樣本服從π(x) 分布。
證明:accept x 服從π(x) 分布,即 p(x|accept) =π(x)。

2. MCMC
給定概率分布 p(x),希望能夠生成它對(duì)應(yīng)的樣本,由于馬氏鏈能收斂到平穩(wěn)分布,有一個(gè)很好的想法:如果我們能構(gòu)造一個(gè)轉(zhuǎn)移矩陣為 P 的馬氏鏈,使得該馬氏鏈的平穩(wěn)分布恰好是p(x),那么我們從任何一個(gè)初始狀態(tài)出發(fā)沿著馬氏鏈轉(zhuǎn)移,得到一個(gè)轉(zhuǎn)移序列 ,如果馬氏鏈在第 n 步已經(jīng)收斂了,于是我們可以得到?p(x) 的樣本?
,如果馬氏鏈在第 n 步已經(jīng)收斂了,于是我們可以得到?p(x) 的樣本? ,所以關(guān)鍵問(wèn)題是如何構(gòu)造轉(zhuǎn)移矩陣 ,我們是基于下面的定理。
,所以關(guān)鍵問(wèn)題是如何構(gòu)造轉(zhuǎn)移矩陣 ,我們是基于下面的定理。
定理1.2(細(xì)致平穩(wěn)條件)如果非周期馬氏鏈的轉(zhuǎn)移矩陣 P 和分布π(x) 滿(mǎn)足:

則π(x) 是馬氏鏈的平穩(wěn)分布。
證明很簡(jiǎn)單,有公式(34)得:

πP=π,滿(mǎn)足馬氏鏈的收斂性質(zhì)。這樣我們就有了新的思路尋找轉(zhuǎn)移矩陣 P,即只要我們找到矩陣 P 使得概率分布π(x) 滿(mǎn)足細(xì)致平穩(wěn)條件即可。
假設(shè)有一個(gè)轉(zhuǎn)移矩陣為 Q 的馬氏鏈(Q(i,j) 表示從狀態(tài) i 轉(zhuǎn)移到狀態(tài) j 的概率),通常情況下很難滿(mǎn)足細(xì)致平穩(wěn)條件的,即:

我們對(duì)公式(36)進(jìn)行改造,使細(xì)致平穩(wěn)條件成立,引入 α (i,j) 。

α(i,j)如何取值才能使公式(37)成立?最簡(jiǎn)單的我們可以取:

Q' (i,j)=Q (i,j)α(i,j) ,Q' (j,i)=Q (j,i)α(j,i) ,所以我們有:

轉(zhuǎn)移矩陣 Q' 滿(mǎn)足細(xì)致平穩(wěn)條件,因此馬氏鏈Q(jìng)' 的平穩(wěn)分布就是π(x)!
我們可以得到一個(gè)非常好的結(jié)論,轉(zhuǎn)移矩陣Q' 可以通過(guò)任意一個(gè)馬氏鏈轉(zhuǎn)移矩陣 Q 乘以α(i,j) 得到, α(i,j)一般稱(chēng)為接受率,其取值范圍為[0,1] ,可以理解為一個(gè)概率值,在原來(lái)的馬氏鏈上,從狀態(tài) i 以Q (i,j) 的概率跳轉(zhuǎn)到狀態(tài) j 的時(shí)候,我們以一定的概率α(i,j) 接受這個(gè)轉(zhuǎn)移,很像前面介紹的接受-拒絕采樣,那里以一個(gè)常見(jiàn)的分布通過(guò)一定的接受-拒絕概率得到一個(gè)不常見(jiàn)的分布,這里以一個(gè)常見(jiàn)的馬氏鏈狀態(tài)轉(zhuǎn)移矩陣Q通過(guò)一定的接受-拒絕概率得到新的馬氏鏈狀態(tài)轉(zhuǎn)移矩陣Q'。

圖1.3
總結(jié)下MCMC的采樣過(guò)程。

MCMC采樣算法有一個(gè)問(wèn)題,如果接受率α(xt,x') 比較小,馬氏鏈容易原地踏步,拒絕大量的跳轉(zhuǎn),收斂到平穩(wěn)分布π(x) 的速度很慢,有沒(méi)有辦法可以使α(xt,x')變大?
3. M-H采樣
M-H采樣可以解決MCMC采樣接受概率過(guò)低問(wèn)題,回到公式(37),若α(i,j)=0.1,α(j,i)=0.2,即:

公式(40)兩邊同時(shí)擴(kuò)大5倍,仍然滿(mǎn)足細(xì)致平穩(wěn)條件,即:

所以我們可以把公式(37)中的α(i,j) 和α(j,i) 同比例放大,使得其中最大的放大到 1,這樣提高了采樣中的接受率,細(xì)致平穩(wěn)條件也沒(méi)有打破,所以可以取:


提出一個(gè)問(wèn)題:按照MCMC中介紹的方法把 Q→Q' ,是否可以保證Q' 每行加和為1?

▌1.10 Gibbs Sampling
對(duì)于高維的情形,由于接受率α≤1,M-H 算法效率不夠高,我們能否找到一個(gè)轉(zhuǎn)移矩陣 Q 使得接受率α=1 呢?從二維分布開(kāi)始,假設(shè)p(x,y) 是一個(gè)二維聯(lián)合概率分布,考察某個(gè)特征維度相同的兩個(gè)點(diǎn) A(x1,y1) 和 B(x1,y2) ,容易發(fā)現(xiàn)下面等式成立:

所以可得:

也就是:

觀察細(xì)致平穩(wěn)條件公式,我們發(fā)現(xiàn)在 x=x1 這條直線上,如果用條件分布p(y|x1) 作為任何兩點(diǎn)之間的轉(zhuǎn)移概率,那么任何兩點(diǎn)之間的轉(zhuǎn)移都滿(mǎn)足細(xì)致平穩(wěn)條件。同樣的,在 y=y1 這條直線上任取兩點(diǎn) A(x1,y1) 和 C(x2,y1) ,我們可以得到:


圖1.4
基于上面的發(fā)現(xiàn),我們可以構(gòu)造分布 p(x,y) 的馬氏鏈的狀態(tài)轉(zhuǎn)移矩陣 Q。

有了上面的轉(zhuǎn)移矩陣 Q ,很容易驗(yàn)證對(duì)于平面任意兩點(diǎn) X,Y,都滿(mǎn)足細(xì)致平穩(wěn)條件。

所以這個(gè)二維空間上的馬氏鏈將收斂到平穩(wěn)分布p(x,y),稱(chēng)為Gibbs Sampling 算法。

整個(gè)采樣過(guò)程中,我們通過(guò)輪換坐標(biāo)軸,得到樣本(x0,y0),(x0,y1),(x1,y1),... ,馬氏鏈?zhǔn)諗亢螅罱K得到的樣本就是p(x,y)的樣本。當(dāng)然坐標(biāo)軸輪換不是必須的,我們也可以每次隨機(jī)選擇一個(gè)坐標(biāo)軸進(jìn)行采樣,在 t 時(shí)刻,可以在 x 軸和 y 軸之間隨機(jī)的選擇一個(gè)坐標(biāo)軸,然后按照條件概率做轉(zhuǎn)移。

圖1.5
二維可以很容易推廣到高維的情況,在 n 維空間中對(duì)于概率分布p(x1,x2,...xn) 。

▌1.11 EM算法
我們先介紹凸函數(shù)的概念,f的定義域是實(shí)數(shù)集,若x∈R且f''(x)≥0,則 f是凸函數(shù),若f''(x)>0,則f是嚴(yán)格凸函數(shù);若x是向量且 hessian 矩陣H是半正定矩陣,則f是凸函數(shù),若H是正定矩陣,則f是嚴(yán)格凸函數(shù)。
定理1.3(Jensen不等式)f的定義域是實(shí)數(shù)集,且是凸函數(shù),則有:

如果f是嚴(yán)格凸函數(shù),只有當(dāng) X 是常量,公式(49)等式成立即E[f(X)]=f(E[X])。

圖1.6
假設(shè)訓(xùn)練集 ,每個(gè)樣本相互獨(dú)立,我們需要估計(jì)模型?p(x,z) 的參數(shù)?θ,由于含有隱變量?z,所以很難直接用最大似然求解,如果?z 已知,那么就可以用最大似然求解。
,每個(gè)樣本相互獨(dú)立,我們需要估計(jì)模型?p(x,z) 的參數(shù)?θ,由于含有隱變量?z,所以很難直接用最大似然求解,如果?z 已知,那么就可以用最大似然求解。

其實(shí)我們的目標(biāo)是找到 z 和θ使 l(θ) 最大,也就是分別對(duì) Z 和θ求偏導(dǎo),然后令其為 0,理想是美好的,現(xiàn)實(shí)是殘酷的,公式(49)求偏導(dǎo)后變的很復(fù)雜,求導(dǎo)前要是能把求和符號(hào)從對(duì)數(shù)函數(shù)中提出來(lái)就好了。EM算法可以有效地解決這個(gè)問(wèn)題,引入 ?表示?
?表示? 的概率分布
的概率分布 。由公式(50)可得:
。由公式(50)可得:

最后一步是利用 Jensen 不等式 所以 f 是凹函數(shù),
所以 f 是凹函數(shù),

是

的期望,所以有:

由公式(51)可知,我們可以不斷地最大化下界,以提高 l(θ),最終達(dá)到最大值。如果固定 θ,那么l(θ) 的下界就取決于 ,可以通過(guò)調(diào)整這個(gè)概率,使得下界不斷地上升逼近 ?l(θ),最終相等,然后固定
,可以通過(guò)調(diào)整這個(gè)概率,使得下界不斷地上升逼近 ?l(θ),最終相等,然后固定 ,調(diào)整 θ,使下界達(dá)到最大值,此時(shí)?θ 為新的值,再固定 θ,調(diào)整
,調(diào)整 θ,使下界達(dá)到最大值,此時(shí)?θ 為新的值,再固定 θ,調(diào)整 ,反復(fù)直到收斂到?l(θ) 的最大值。現(xiàn)在我們有兩個(gè)問(wèn)題需要證明,1. 下界何時(shí)等于 l(θ);2. 為什么可以收斂到最大值。
,反復(fù)直到收斂到?l(θ) 的最大值。現(xiàn)在我們有兩個(gè)問(wèn)題需要證明,1. 下界何時(shí)等于 l(θ);2. 為什么可以收斂到最大值。
第一個(gè)問(wèn)題,由Jensen不等式定理中等式成立條件可知,X 為常量,即:

再由 得:
得:

下面我們先給出 EM 算法,然后再討論第二個(gè)問(wèn)題,E步:固定 θ,根據(jù)公式(53)選擇 Qi 使得下界等于 l(θ),M步:最大化下界,得到新的θ 值。EM算法如下:

在我們開(kāi)始討論第二個(gè)問(wèn)題, 是EM迭代過(guò)程的參數(shù)估計(jì),我們需要證明
是EM迭代過(guò)程的參數(shù)估計(jì),我們需要證明 ,也就是EM算法是單調(diào)地提高
,也就是EM算法是單調(diào)地提高 。
。

第一個(gè)不等式是因?yàn)椋?/p>

公式(57)中, 。
。
第二個(gè)不等式是因?yàn)?img src="http://file.elecfans.com/web1/M00/56/E3/pIYBAFtDB3SAJf3wAAADKq_0JMI797.png" />是為了

三、LDA
▌2.1 Unigram Model
假設(shè)我們的詞典中一共有 V 個(gè)詞,Unigram Model就是認(rèn)為上帝按照下面游戲規(guī)則產(chǎn)生文本的。


Game 2.1 Unigram Model
骰子各個(gè)面的概率記為 ,對(duì)于一篇文檔
,對(duì)于一篇文檔 ,生成該文檔的概率為:
,生成該文檔的概率為:

假設(shè)我們預(yù)料是由 m 篇文檔組成即 ,每篇文檔是相互獨(dú)立的,則該預(yù)料的概率為:
,每篇文檔是相互獨(dú)立的,則該預(yù)料的概率為:

假設(shè)預(yù)料中總共有 N 個(gè)詞,每個(gè)詞 wi 的詞頻為 ni,那么 服從多項(xiàng)式分布,可參考1.5節(jié)的多項(xiàng)式分布概念。
服從多項(xiàng)式分布,可參考1.5節(jié)的多項(xiàng)式分布概念。

此時(shí)公式(60)為:

我們需要估計(jì)模型中的參數(shù) ,可以用最大似然估計(jì):
,可以用最大似然估計(jì):

于是參數(shù) pk 的估計(jì)值就是:

▌2.2 貝葉斯Unigram Model
對(duì)于以上模型,統(tǒng)計(jì)學(xué)家中貝葉斯學(xué)派就不同意了,為什么上帝只有一個(gè)固定的篩子呢,在貝葉斯學(xué)派看來(lái),一切參數(shù)都是隨機(jī)變量,模型中 不是唯一固定的,而是服從一個(gè)分布,所以貝葉斯Unigram Model游戲規(guī)則變?yōu)椋?/p>
不是唯一固定的,而是服從一個(gè)分布,所以貝葉斯Unigram Model游戲規(guī)則變?yōu)椋?/p>


Game 2.2 貝葉斯Unigram Model
上帝這個(gè)壇子里面有些骰子數(shù)量多,有些骰子數(shù)量少,所以從概率分布的角度看,壇子里面的骰子 服從一個(gè)概率分布
服從一個(gè)概率分布 ,這個(gè)分布稱(chēng)為參數(shù)
,這個(gè)分布稱(chēng)為參數(shù) 的先驗(yàn)分布。先驗(yàn)分布?
的先驗(yàn)分布。先驗(yàn)分布?
 是服從多項(xiàng)式分布的,
是服從多項(xiàng)式分布的, ,回顧1.7節(jié)可知,
,回顧1.7節(jié)可知, 

于是,在給定了參數(shù)
 時(shí)候,語(yǔ)料中各個(gè)詞出現(xiàn)的次數(shù)服從多項(xiàng)式分布
時(shí)候,語(yǔ)料中各個(gè)詞出現(xiàn)的次數(shù)服從多項(xiàng)式分布 ,所以后驗(yàn)分布為:
,所以后驗(yàn)分布為:

對(duì)參數(shù)


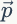

 分布。可以用? 的期望值作為參數(shù)?
分布。可以用? 的期望值作為參數(shù)?


接下來(lái)我們計(jì)算語(yǔ)料產(chǎn)生的概率,開(kāi)始并不知道上帝到底用哪個(gè)骰子,所以每個(gè)骰子都有可能被使用,使用的概率由 決定的,對(duì)于每個(gè)具體的骰子,由該骰子產(chǎn)生預(yù)料的概率為
決定的,對(duì)于每個(gè)具體的骰子,由該骰子產(chǎn)生預(yù)料的概率為 ,所以語(yǔ)料產(chǎn)生的概率為:
,所以語(yǔ)料產(chǎn)生的概率為:

▌2.3 PLSA
1. PLSA Model
概率隱語(yǔ)義分析,是主題模型的一種。上面介紹的Unigram Model相對(duì)簡(jiǎn)單,沒(méi)有考慮文檔有多個(gè)主題的情況,一般一篇文檔可以由多個(gè)主題(Topic)組成,文檔中的每個(gè)詞都是由一個(gè)固定的Topic生成的,所以PLSA的游戲規(guī)則為:

2. EM算法推導(dǎo)PLSA
PLSA 模型中 doc-topic 和 topic-word 的每個(gè)面的概率值是固定的,所以屬于點(diǎn)估計(jì),但是PLSA模型既含有觀測(cè)變量di,wj,又含有隱變量 zk,就不能簡(jiǎn)單地直接使用極大似然估計(jì)法估計(jì)模型參數(shù),我們可以采用EM算法估計(jì)參數(shù)。我們先介紹推導(dǎo)過(guò)程用到的符號(hào)含義:
 :表示語(yǔ)料中 N 篇文檔;
:表示語(yǔ)料中 N 篇文檔;
 :表示語(yǔ)料中 M 個(gè)詞組;
:表示語(yǔ)料中 M 個(gè)詞組;
 :表示詞 wj 在文檔 di 中出現(xiàn)的頻次,
:表示詞 wj 在文檔 di 中出現(xiàn)的頻次, ;
;
 :表示 K 個(gè)主題,每篇文檔可以有多個(gè)主題;
:表示 K 個(gè)主題,每篇文檔可以有多個(gè)主題;
 wj 在給定文檔?di 中出現(xiàn)的概率;
wj 在給定文檔?di 中出現(xiàn)的概率;
 :表示主題 zk 在給定文檔?di 下出現(xiàn)的概率;
:表示主題 zk 在給定文檔?di 下出現(xiàn)的概率;
 :表示詞?wj? 在給定主題?zk 下出現(xiàn)的概率。
:表示詞?wj? 在給定主題?zk 下出現(xiàn)的概率。
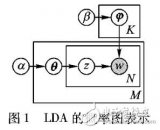
一般給定語(yǔ)料di,wj是可以觀測(cè)的,zk 是隱變量,不可以直觀地觀測(cè)到。我們定義“doc-word”的生成模型,如圖1.8所示。


圖2.3
下面進(jìn)入正題,用EM算法進(jìn)行模型參數(shù)估計(jì),似然函數(shù)為:

對(duì)于給定訓(xùn)練預(yù)料,希望公式 (69) 最大化。 


引入 表示 zk 的概率分布
表示 zk 的概率分布

,根據(jù)Jensen不等式得:

當(dāng)

時(shí),
公式(71)不等式中等號(hào)成立,所以只需要最大化:

根據(jù)拉格朗日乘子法

所以可得:

總結(jié)EM算法為:
1.E-step 隨機(jī)初始化變量 , 計(jì)算隱變量后驗(yàn)概率。
計(jì)算隱變量后驗(yàn)概率。

2.M-step 最大化似然函數(shù),更新變量 ,
,

3.重復(fù)1、2兩步,直到收斂。
▌2.4 LDA
對(duì)于 PLSA 模型,貝葉斯學(xué)派表示不同意,為什么上帝只有一個(gè) doc-topic 骰子,為什么上帝只有固定 K 個(gè)topic-word骰子? 是模型的參數(shù),一切參數(shù)都是隨機(jī)變量,模型中
是模型的參數(shù),一切參數(shù)都是隨機(jī)變量,模型中 不是唯一固定的,類(lèi)似 2.2 節(jié)貝葉斯 Unigram Model 和 2.1 節(jié) Unigram Model 的關(guān)系。所以 LDA 游戲規(guī)則為:
不是唯一固定的,類(lèi)似 2.2 節(jié)貝葉斯 Unigram Model 和 2.1 節(jié) Unigram Model 的關(guān)系。所以 LDA 游戲規(guī)則為:

假設(shè)我們訓(xùn)練語(yǔ)料有 M 篇 doc,詞典中有 V 個(gè)word,K 個(gè)topic。對(duì)于第m 篇文檔有 Nm 個(gè)詞。
 ,第 m 篇文檔的主題分布概率,
,第 m 篇文檔的主題分布概率,

;
 ,主題為 k 的詞的概率分布,
,主題為 k 的詞的概率分布, ;
;
 :第 m 篇文檔中屬于 topic k 的詞的個(gè)數(shù),
:第 m 篇文檔中屬于 topic k 的詞的個(gè)數(shù),

;
 :topic k 產(chǎn)生詞 t 的個(gè)數(shù),
:topic k 產(chǎn)生詞 t 的個(gè)數(shù),

;
 :
: 先驗(yàn)分布超參數(shù);
先驗(yàn)分布超參數(shù);
 :
: 先驗(yàn)分布超參數(shù);
先驗(yàn)分布超參數(shù);
 :第 m 篇文檔中第 n 個(gè)詞的主題;
:第 m 篇文檔中第 n 個(gè)詞的主題;
 :第 m 篇文檔中第 n 個(gè)詞。
:第 m 篇文檔中第 n 個(gè)詞。
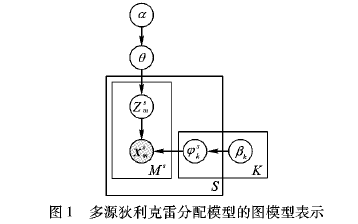
LDA的概率圖模型表示如圖2.4所示。

圖2.4
1. 聯(lián)合概率分布

1) :第一步對(duì)?
:第一步對(duì)? 分布進(jìn)行采樣得到樣本
分布進(jìn)行采樣得到樣本 (也就是從第一個(gè)壇子中抽取 doc-topic 骰子 );第二步 doc-topic 骰子有 K 個(gè)面,每個(gè)面表示一個(gè)主題,那么在一次投擲骰子過(guò)程中,每個(gè)主題的概率為
(也就是從第一個(gè)壇子中抽取 doc-topic 骰子 );第二步 doc-topic 骰子有 K 個(gè)面,每個(gè)面表示一個(gè)主題,那么在一次投擲骰子過(guò)程中,每個(gè)主題的概率為

,第 m 篇文檔有Nm個(gè)詞,所以需要投擲Nm 次骰子,為該篇文檔中的每個(gè)詞生成一個(gè)主題, 第 n 個(gè)詞對(duì)應(yīng)的主題為
,整篇文檔的主題表示為 。在?Nm 次投擲過(guò)程中,每個(gè)主題出現(xiàn)的次數(shù)為
。在?Nm 次投擲過(guò)程中,每個(gè)主題出現(xiàn)的次數(shù)為

,那么 服從多項(xiàng)式分布
服從多項(xiàng)式分布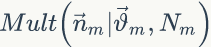 (只生成每個(gè)詞的主題,并未由主題產(chǎn)生具體的詞)。可以采用貝葉斯估計(jì)對(duì)參數(shù)?
(只生成每個(gè)詞的主題,并未由主題產(chǎn)生具體的詞)。可以采用貝葉斯估計(jì)對(duì)參數(shù)? 進(jìn)行估計(jì)。
進(jìn)行估計(jì)。
 ?的先驗(yàn)分布為?
?的先驗(yàn)分布為?
后驗(yàn)分布為(推導(dǎo)過(guò)程可以參考1.7節(jié))

 的貝葉斯估計(jì)值為
的貝葉斯估計(jì)值為

下面我們計(jì)算第 m 篇文檔的主題概率分布:

整個(gè)語(yǔ)料中的 M 篇文檔是相互獨(dú)立的,所以可以得到語(yǔ)料中主題的概率為:

2)

:第一步對(duì) 分布進(jìn)行 K?采樣得到樣本
分布進(jìn)行 K?采樣得到樣本 (從第二個(gè)壇子中獨(dú)立地抽取了 K 個(gè)topic-word骰子
(從第二個(gè)壇子中獨(dú)立地抽取了 K 個(gè)topic-word骰子 );第二步根據(jù)之前得到的主題
);第二步根據(jù)之前得到的主題 ,為每個(gè)?
,為每個(gè)? 生成對(duì)應(yīng)的詞
生成對(duì)應(yīng)的詞 ,
,


,第 k 個(gè)主題有 個(gè)詞,所以需要投擲?
個(gè)詞,所以需要投擲?



,那么 服從多項(xiàng)式分布
服從多項(xiàng)式分布 ,可以采用貝葉斯估計(jì)對(duì)參數(shù)?
,可以采用貝葉斯估計(jì)對(duì)參數(shù)? 進(jìn)行估計(jì)。
進(jìn)行估計(jì)。
 的先驗(yàn)分布為?
的先驗(yàn)分布為?
 后驗(yàn)分布為(推導(dǎo)過(guò)程可以參考1.7節(jié))
后驗(yàn)分布為(推導(dǎo)過(guò)程可以參考1.7節(jié))

 的貝葉斯估計(jì)值為
的貝葉斯估計(jì)值為

下面我們計(jì)算第k 個(gè)主題的詞概率分布:

整個(gè)語(yǔ)料中的 K 個(gè)主題是相互獨(dú)立的,所以可以得到語(yǔ)料中詞的概率為:

由公式(74)、(78)、(82) 可得聯(lián)合概率分布為:

2. Gibbs Sampling
上面我們已經(jīng)推導(dǎo)出參數(shù)的貝葉斯估計(jì)公式,但是仍然存在一個(gè)問(wèn)題,公式中的 無(wú)法根據(jù)語(yǔ)料直接得到,如果我們知道語(yǔ)料中的每個(gè)詞的主題,即得到
無(wú)法根據(jù)語(yǔ)料直接得到,如果我們知道語(yǔ)料中的每個(gè)詞的主題,即得到 ,那么就可以推斷出
,那么就可以推斷出 ,進(jìn)一步就可以得出貝葉斯的參數(shù)估計(jì)。我們需要利用 Gibbs Sampling 對(duì)?
,進(jìn)一步就可以得出貝葉斯的參數(shù)估計(jì)。我們需要利用 Gibbs Sampling 對(duì)? 進(jìn)行采樣來(lái)得到
進(jìn)行采樣來(lái)得到 
 。 先介紹一些符號(hào)定義。
。 先介紹一些符號(hào)定義。
 下標(biāo)索引;
下標(biāo)索引;
 :表示去除下標(biāo)為 i 的詞;
:表示去除下標(biāo)為 i 的詞;
 :第 m 篇文檔中第 n 個(gè)詞為 t;
:第 m 篇文檔中第 n 個(gè)詞為 t;
 :第 m 篇文檔中第 n 個(gè)詞的主題為 k;
:第 m 篇文檔中第 n 個(gè)詞的主題為 k;
 :除去下標(biāo)為 i 這個(gè)詞,剩下的所有詞中,詞 t 屬于主題 k 的統(tǒng)計(jì)次數(shù),
:除去下標(biāo)為 i 這個(gè)詞,剩下的所有詞中,詞 t 屬于主題 k 的統(tǒng)計(jì)次數(shù),

(這里假設(shè) );
);
 :除去下標(biāo)為 i 的這個(gè)詞,第 m 篇文檔中主題 m 產(chǎn)生詞的個(gè)數(shù),?
:除去下標(biāo)為 i 的這個(gè)詞,第 m 篇文檔中主題 m 產(chǎn)生詞的個(gè)數(shù),?

(這里假設(shè) );
); :語(yǔ)料的主題;
:語(yǔ)料的主題;
 :語(yǔ)料的單詞。
:語(yǔ)料的單詞。

1) 的計(jì)算過(guò)程類(lèi)似
的計(jì)算過(guò)程類(lèi)似 ,僅僅在計(jì)算的時(shí)候不考慮下標(biāo)為 i 的這個(gè)詞,我們假設(shè)
,僅僅在計(jì)算的時(shí)候不考慮下標(biāo)為 i 的這個(gè)詞,我們假設(shè) ;當(dāng)已知語(yǔ)料時(shí),
;當(dāng)已知語(yǔ)料時(shí), 可以從語(yǔ)料中統(tǒng)計(jì)出來(lái),所以可以認(rèn)為是常量。
可以從語(yǔ)料中統(tǒng)計(jì)出來(lái),所以可以認(rèn)為是常量。

2)我們是推斷 i=(m,n)詞 t 的主題為 k 的條件概率
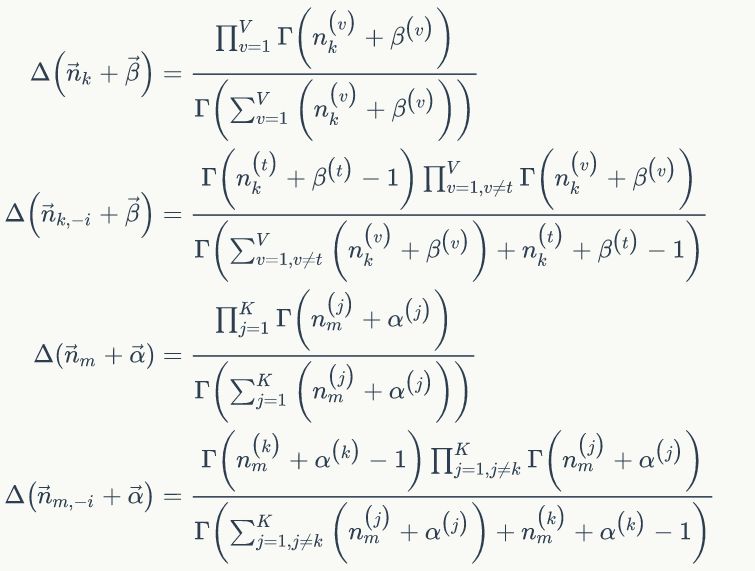
我們?cè)倮昧硗庖环N方法推導(dǎo)條件概率:

已經(jīng)推導(dǎo)出條件概率,可以用Gibbs Sampling公式進(jìn)行采樣了。

-
函數(shù)
+關(guān)注
關(guān)注
3文章
4345瀏覽量
62868 -
文本分類(lèi)
+關(guān)注
關(guān)注
0文章
18瀏覽量
7337 -
LDA
+關(guān)注
關(guān)注
0文章
29瀏覽量
10635
原文標(biāo)題:干貨 | 一文詳解隱含狄利克雷分布(LDA)
文章出處:【微信號(hào):AI_Thinker,微信公眾號(hào):人工智能頭條】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
狄拉克量子力學(xué)

基于LDA主題模型的移動(dòng)應(yīng)用的相似度矩陣
大規(guī)模分布式機(jī)器學(xué)習(xí)系統(tǒng)分析

基于隱含狄列克雷分配LDA分類(lèi)特征擴(kuò)展的廣告過(guò)濾方法
一種融合圖像紋理結(jié)構(gòu)信息的LDA扣件檢測(cè)模型
一種細(xì)粒度的面向產(chǎn)品屬性的用戶(hù)情感模型
基于LDA主題模型進(jìn)行數(shù)據(jù)源選擇方法
如何使用狄利克雷多項(xiàng)分配模型進(jìn)行多源文本主題挖掘模型
基于狄利克雷問(wèn)題的動(dòng)態(tài)劃分算法
基于狄利克雷過(guò)程的可擴(kuò)展高斯混合模型





 一文詳解隱含狄利克雷分布(LDA)
一文詳解隱含狄利克雷分布(LDA)











評(píng)論