無論有沒有去過賭場，相信大多數人都不會對老虎機感到陌生。作為賭場里最常見的娛樂設備，老虎機不僅在現實中廣受人們歡迎，它也頻繁出現在電視電影乃至動畫片中，連一些常見的APP里都有它的身影。

往機器里投入硬幣后，玩家需要拉下拉把轉動玻璃框中的圖案，如果三個圖案一致，玩家能獲得所有累積獎金；如果不一致，投入的硬幣就會被吞入累積獎金池。這個問題看似簡單，但很多人也許都忽視了，其實它和圍棋、游戲一樣，也是個強化學習問題。

首先，我們要明確一點——老虎機問題是表格型解決方案工具的一種。之所以這么說，是因為我們可以把所有可能的狀態放進一個表格中，然后讓表格告訴我們需要了解的問題狀態，繼而為解決問題找出切實的解決方案。

k-armed Bandit Problem

單臂老虎機：只有一根側面拉桿

假設我們有一臺K臂老虎機，每根拉桿都能提供固定的一定數額的金錢，一次只能拉下一根拉桿，但我們不知道它們的具體回報是多少。在這個情景中，k根拉桿可以被視為k種不同的動作（action），拉下拉桿的總次數T是我們的總timestep。整個任務的目標是實現收益的最大化。

設在第t次拉下拉桿時，我們采取的動作是At，當時獲得的回報是Rt。那么對于任意動作a，它的動作值（value）q?(a)是：

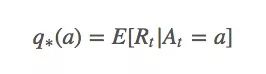
這個等式表示的是無論何時，如果我們選擇動作a，我們獲得的實際回報就應該等于動作a的預期回報。

把上面這個句子再讀三四遍，你覺得它行得通嗎？如果我們事先已經知道拉下這個拉桿的最大收益是多少，那出于貪婪的目的，我們肯定每次都會選最好的動作，然后使最終回報最大化。但在強化學習問題中，貪婪算法并不一定等同于最優策略，這一步的貪婪可能會對下一步產生負面影響。

雖然很困難，但我們真的很想實現q?(a)，所以對于timestep t，設Qt(a)是q?(a)的近似值：

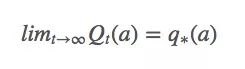
那么我們又該怎么獲得Qt(a)？

注：上文中的回報（reward）和動作值（value）不是同一個概念。回報指的是執行動作后的當場回報，動作值是一個長期的回報。如果你吸毒了，一小時內你很high，回報很高，但長期來看，你獲得的動作值就很可怕了。需要注意的是，因為賭博機只需要一個動作，所以這里的q?(a)不是未來回報之和，只是期望回報，它和其他地方的q?(a)也不一樣（雖然有濫用符號之嫌，但還是請多包涵啦）。

動作值方法

函數Qπ(x, a)表示從狀態x出發，執行動作a后再使用策略π帶來的累計獎賞，稱為“狀態-動作值函數”（state-action value function）。——周志華《機器學習》

首先，我們需要估計動作值，再據此決定要采取的行動。

估算動作值

求解q?(a)近似值的一種簡單方法是使用樣本平均值：

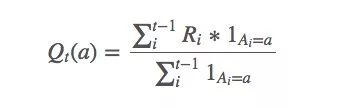
上述等式看起來好像有什么說法，但它其實很簡單——選擇動作a時，我們獲得的平均回報是多少。這個均值可以被視為q?(a)的近似值，因為換幾個符號，我們就能發現這就是強大數定律（SLLN）的表達式。

換句話說，它意味著Qt(a)必須收斂于q?(a)：

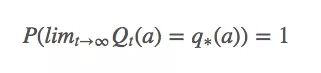
比起概率收斂，這種收斂更強大，但它其實也沒法保證Qt(a)一定能收斂。

動作選擇規則：貪婪

“貪婪者總是一貧如洗。”當面對巨大誘惑時，一些人會因為貪婪越過自己的底線，去吸毒，去犯罪，但他們在獲得短暫快感的同時也失去了更多東西。強化學習中同樣存在類似的問題，如果它是貪婪的，它會找出迄今為止最大的動作值：

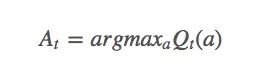
并依據這個動作值去選擇每一步動作。這樣做的后果是智能體從頭到尾只會選擇同一套動作，而從不去嘗試其他動作，在很多情況下，這樣的策略并不是最優策略。

動作選擇規則：?-Greedy

那么我們該怎么糾正它的貪婪？之前我們在《強化學習——蒙特卡洛方法介紹》一文中已經介紹過ε-greedy：對于任何時刻t的執行“探索”小概率ε<1，我們會有ε的概率會進行exploration，有1-ε的概率會進行exploitation。這可以簡單理解成拋硬幣，除了正面和反面，它還有一個極小的立起來的概率。

雖然當智能體“頭腦發熱”時，它還是會義無反顧地貪婪，但相比貪婪策略，?-Greedy隨機選擇策略（不貪婪）的概率是ε/|A(s)|。

癥結：非平穩的動作值

導致這種現象的主要原因是動作值會隨時間推移發生變化，即之前我們研究的時靜態地拉桿，而不是隨機的、動態的拉桿。以動作值為例，比起我們之前假設的q?(a)，它更應該被表示成q?(a, t)。

依據之前的動作值估計，我們有：

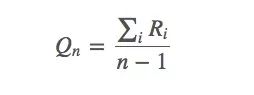
它也可以被寫成：

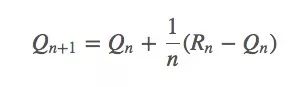
看起來SGD可以在這里發揮一些作用。如果它是平穩的，那q?(a)收斂的概率就是100%；如果它不平穩，我們一般不會希望Rn=Rn-1，因為當前回報會影響當前的動作值。

這里我們把權重1/n替換成α（α∈(0,1]）：

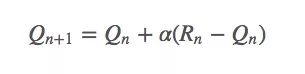
這是一個指數平均值，它在幾何上衰減之前回報的權重。設函數αn(a)是第n個timestep，也就是第n次拉下拉桿時某個特定獎勵的權重。因為老虎機問題只需考慮動作a，所以這個函數也可以簡化成α(a)。

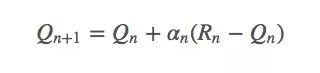
為了保證上式能收斂，我們還需要一些其他條件。

條件一

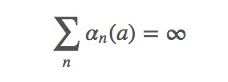
上式表示對于任何初始值Q1∈?，它都滿足q?(a)∈?。這個條件要求保證timestep足夠大，以最終克服任何初始條件或隨機波動

條件二

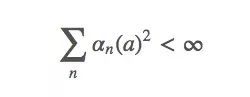
這個式子表示這些timestep將“足夠小以確保能收斂到一個小值”。簡而言之，第二個條件保證最終timestep會變小，以保證收斂。

既然如此，我們之前為什么要設αn(a)=α∈(0,1]呢？它不是一個常數嗎？這樣的閾值會不會影響收斂？

這些猜想都是正確的，但(0,1]這個閾值也有它存在的價值。我們在之前的Qn+1=Qn+αn(Rn+Qn)上繼續計算，最后可以獲得一項α(1-α)n-iRi，因為α小于1，所以給予R的權重隨著介入獎勵次數的增加而減少。

因為最佳動作值時非平穩的，所以我們不想收斂到一個特定的價值。

動作選擇規則：樂觀的初始值

到目前為止，我們必須非常隨意地設定Q1(a)的初始值，它本質上是一組用于初始化的超參數。這里有個小訣竅，我們可以設初始值Q1(a)=C?a，其中C>q?(a)?a。

這樣之后，因為Qn(a)比估計值偏高，這時智能體會積極探索其他動作，當它越來越接近q?(a)時，智能體就開始貪婪了。換句話說，假設我們設當前拉桿的樂觀回報是3，但智能體嘗試一次后，發現回報只有1，低于預期值，于是它會把其他拉桿全部嘗試一遍。雖然前期效率很低，但到后期，智能體已經掌握哪些拉桿會產生高值，效果就接近“貪婪”了。

這種方法時可行的，在某種程度上，如果時間充裕，這個過程也可以被看作是模擬退火。但從整體來看，樂觀初始值前期的大量“exploration”是不必要的，它對于非平穩問題來說不是最好的答案。

動作選擇規則：置信上限選擇

在機器學習系統中，Bias與Variance往往不可兼得：如果要降低模型的Bias，就一定程度上會提高模型的Variance；如果要降低Variance，Bias就會不可避免地提高。針對兩者間的trade-off，下面的式子是一個很好的總結：

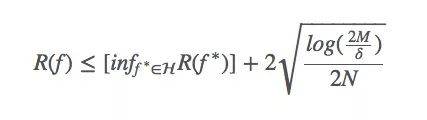
其中，

R(f)是假設f的（理論上）的風險；

R(f< *)是在假設集H中，假設f的最小風險；

M是假設集|H|的大小；

N是其中的樣本數；

δ是一個常數（如果非要知道這個常數是什么，只能說它是我們選擇一個差的假設的概率）。

這里有兩個重點：

樣本數量非常少，我們的邊界非常松散。我們不知道目前的假設是否是最好的假設。

我們的假設越大，PAC（近似正確）學習的約束就越松散。

置信上限（UCB）是一個非常強大的算法，它可以用類似Bias-Variance權衡的方法來解決不同的問題。在老虎機問題中，我們可以把timestep t當成假設集大小M，因為隨著t逐漸增加，an也會逐漸增加，相應的At就很難選擇。

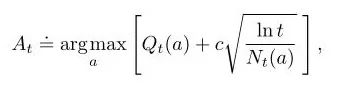
每選一次a，不確定項就會減少，分母Nt(a)增加；另一方面，每一次選擇了a以外的行為，t會增加但Nt(a)不會改變，不確定評估值會增加。

梯度老虎機算法

截至目前，我們一直在努力估計q?(a)，但如果說這個問題還有除了行動值以外的解決方法呢？比如我們該如何學習一個動作的偏好？

設動作偏好為Ht(a)，它和回報無關，只是一個動作相對于另一個動作的重要性。那么At應該符合gibbs分布（也就是機器學習的softmax分布）：

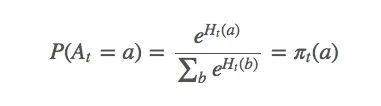
對于這個式子，我們該怎么基于梯度計算最大似然估計？首先，我們對Ht(a)做梯度上升，因為它是我們的變量。我們想最大化E(Rt)：

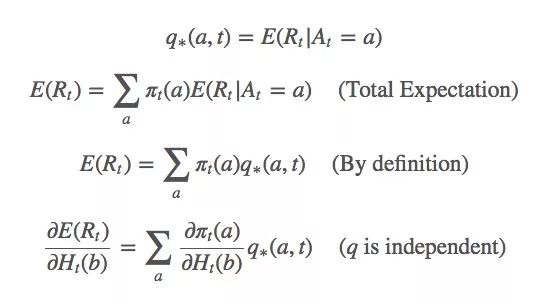
Ht(a)的更新規則如下所示：

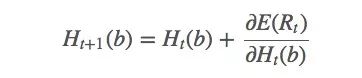
gibbs分布分解：

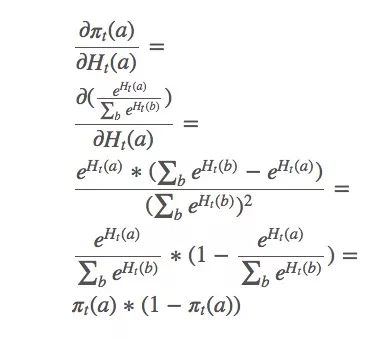
這只是整個梯度的一個偏導數。那么b≠a的動作呢？下面是省略計算過程的結果：

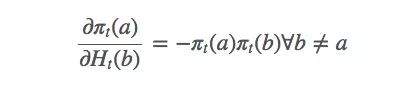
由此可得：

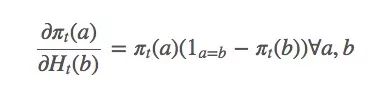
因為：

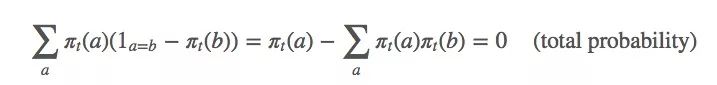
相應的，這個等式也是成立的：

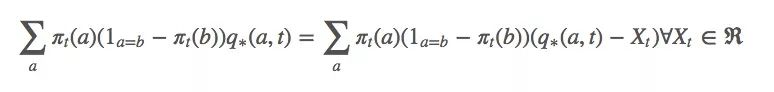
由上述等式可得：

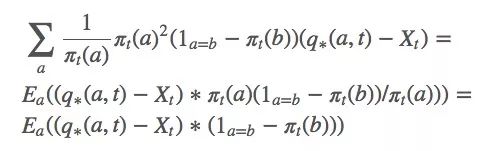
因為q?(a,t)被包含在動作a的預期值內，它也可以被寫成Rt。那等式里的Xt是什么？坦率地說，你想它是什么它就是什么，嚴謹起見，我們可以設Xt是Rt的平均值。

計算梯度后獲得新的更新規則：

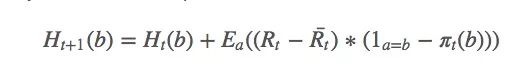
其中a是t時采取的動作。由于找到a的期望值很困難，我們可以用隨機值來更新：

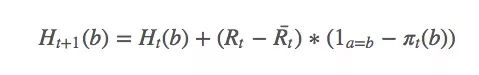
選擇動作的簡單方法是計算argmaxaπt(a)，問題就解決了。

備注

下面是上述算法的一個比較圖：

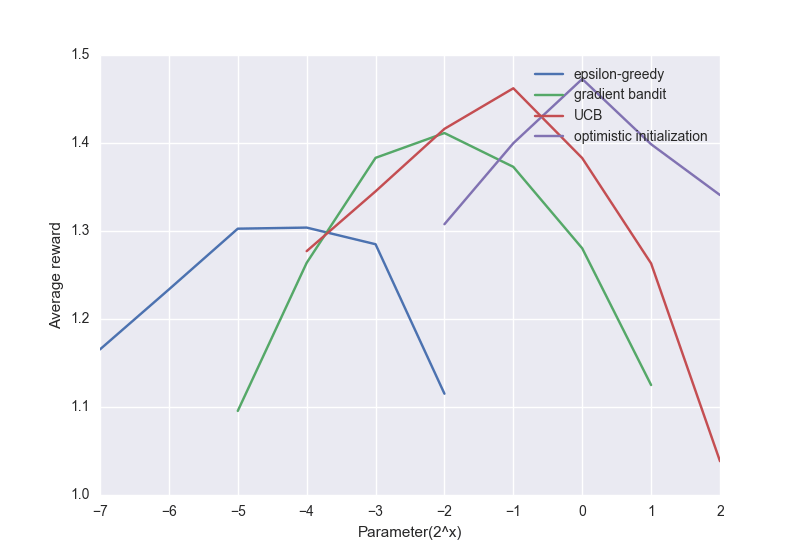
盡管簡單的方法表現不太好，但對很多強化學習問題來說，它們也稱得上是最先進的算法了。