筆者多年來反復用一道面試題來考察IC求職人員的水平和能力。這道面試題看似平淡無奇，大部分求職者卻只知其一不知其二，知其然而不知其所以然。這是一道怎樣的奇葩題目呢：

請設計一個異步復位的計數器：“從0到20的無限循環計數，每次計數到20便清0從頭開始計數。”

看到這里有沒有心想“Are you kidding me? So simple?”？其實不然，對于初學者而言，這其實是一個連環無敵面試題。欲知詳情，請見本文一一拆解。

問題1：如何用Verilog實現這個計數器？

針對上述功能的計數器，應該如何用Verilog實現？

一般而言，大多數學過Verilog語言的人，這一個問題都能回答清楚，初步的解題思路如下：

模塊有2個輸入：時鐘clk，復位rst_n（此處用下降沿有效的復位為例）

模塊有1個輸出：每次計數到20時，輸出信號cnt_timeout拉起一拍

完整的Verilog代碼如下：

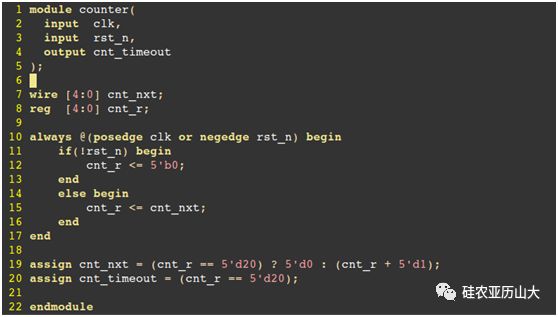
問題2：此計數器代表的實際電路是什么？

在面試的學生回答出如何用Verilog實現計數器后，第二個問題筆者就會問：

用Verilog實現的這個計數器背后的實際電路是什么？如果給你提供多個D觸發器，多個比較器，多個加法器，多個多路選擇器，你怎么組合出這個電路？

經過筆者的實驗統計，這個問題大概有30%的人能不假思索的回答出來，剩下的大概20%在經過引導后也能說出自己的思路和答案，而經過引導也沒有思路的50%則存在著“只知語法不知電路”的問題，需要進一步學習提高。

完整電路如下：

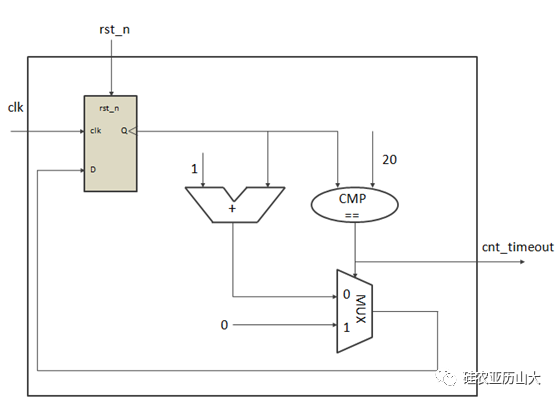
問題3：此計數器的關鍵路徑是哪一條？

初學者如果能夠回答出上一個問題，那么說明對于電路的理解已經相當的不錯，那么接下來的問題便是 ：“以上電路的關鍵路徑在哪里”？

絕大多數的面試學生對于這個問題是難以回答的，主要原因是，不理解關鍵路徑的含義，或者找不出關鍵路徑。

正確答案如下：關鍵路徑應該是從“寄存器的Q端”->加法器（ADD）->多路選擇器（MUX）->“寄存器的D端”。

有關關鍵路徑（Critical Path）的概念需要初學者自行查閱學習。

如果能夠回答出上述問題，那么可以繼續反問面試學生：為什么關鍵路徑不是從“寄存器的Q端”->比較器（CMP）->多路選擇器（MUX）->“寄存器的D端”。即：比較器（CMP）和加法器（ADD）哪個更關鍵，有關此問題，請參見后續問題。

問題4：“cnt == 20”對應的電路是什么？

上述電路中的比較器其實是“cnt == 20”，那么這段比較器代碼對應的電路是什么呢？此問題非常簡單，但是絕大多數初學者是回答不出來的。

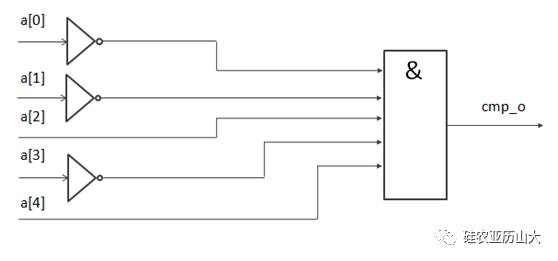
正確答案：20的2進制表示為5’b10100，那么“等于”20的電路邏輯如下圖所示，即對應0的位取反，對應1的位不取反，將其與在一起。此乃大二數電的基本知識。

注意：只有“等于”常數才能得到如此簡潔的電路，如果是兩個變量的“等于”比較則必須使用“同或”電路來實現，“同或”電路是什么邏輯？查一查大二數電的基本知識。

問題5：使用“cnt > 19”和“cnt == 20”一樣嗎？

針對上述電路中的比較器，接下來的問題是 ：“用cnt > 19來代替cnt == 20行嗎？ 為什么”？

一個對電路有深刻理解的人應該不僅僅能回答出行不行，還能說出為什么。

正確答案如下：功能上是可行，但從電路優化的角度看，是不行的。

因為“cnt == 20”如上文所述，實現相對簡單，用少量的非門及與門即可實現。但“cnt > 19” 的電路邏輯更為復雜。

具體的“cnt > 19”的電路是怎樣的呢？對于這個5bit的“cnt > 19”， cnt可能的范圍取值為[20:31]，綜合工具會將電路優化成幾個等于相與：“cnt == 20 && cnt == 21 && …… && cnt == 31”。顯然“cnt > 19”的電路實現比“cnt == 20”復雜許多。所以此處用“cnt > 19”是不合適的，會帶來額外的硬件開銷。

上述5 bit的大于的比較電路，因為cnt的可能的取值范圍是[20:31]，綜合工具能將電路優化成幾個等于相與，但假設cnt是32 bit的，那“cnt > 19”所代表的cnt的可能的取值范圍太大，此時對于32bit的“cnt > 19”，則相當于“cnt – 19 > 0”，此比較器映射的電路將引入一個加法器。

問題6：加法器的電路是什么？

加法器的電路比較復雜，以后的系列會專門講加法器：“登堂設計案例之：加法器真的就是寫個+號這么簡單嗎？”。

但有一點是可以肯定的：如采用“cnt==20”的比較器，上述計數器中的加法器的延時肯定是大于比較器的。

所以，關鍵路徑是上面所述的“寄存器的Q端”->加法器（ADD）->多路選擇器（MUX）->“寄存器的D端”。

附加問題：如何驗證這個計數器？

如果學生是面試IC驗證工程師崗位的，此時不妨加上一些驗證相關的問題：

如何驗證這個計數器？

你的TB的組成是怎樣的？

列舉一下針對這個計數器功能描述提取的測試點？由于此系列以Verilog設計為主要講解主題，所以驗證的問題在此不深入展開討論。

基于這個簡單的計數器，您還能想出什么衍生問題可以加入這一系列的面試題呢？

結語

最后，我們總結下核心要義：Verilog只是一種硬件描述語言，IC設計的本質是對于電路的設計，雖然現在Verilog Coding采用RTL級別的抽象描述，但是必須清楚所描述的代碼能夠映射出的電路結構，對其面積和時序的影響都了然于胸，只有如此才能夠成為一名優秀的IC設計工程師。