功率電子轉換器可以視為由分段線性元件(傳統元件如電阻、電感和電容是特例)與電壓源、電流源、二極管和電子開關(如晶閘管、晶體管、MOSFET等)組成。
在此背景下,我們將電子設備(ED)定義為任何具有分段線性電流-電壓特性的電氣或電子元件,盡管這可能是一個不太精確的術語。在許多實際情況下,電子設備可以建模為一個可變電阻,其在導通狀態下的值非常低,而在阻斷狀態下的值非常高。在其他情況下,可能需要使用更詳細的半導體模型來表示設備。然而,在系統層面,特別是在建模、仿真和控制設計中,快速切換現象通常不是主要關心的問題。在這些情況下,將二極管和開關視為理想元件更為便利,假設它們在實質上瞬間在打開和關閉狀態之間切換。
這種特性賦予了系統模型一種混合性質,結合了離散和連續時間元素。因此,開關電子系統被歸類為混合系統。這些系統通過多種拓撲或模式運行,具體取決于開關設備的狀態。因此,有必要區分轉換器的不同模式,為每種模式開發線性時不變動態模型,并定義系統在模式之間切換的條件。由此過程得到的模型通常被稱為開關模型,這是許多功率轉換器仿真器(如PLECS)使用的框架。不幸的是,切換的條件可能依賴于狀態變量(稱為內部控制換相),這使得開關模型變得越來越復雜,即使對于相對簡單的轉換器拓撲也是如此。
一般來說,構建一個涵蓋所有可能操作條件的開關模型(稱為完整開關模型)對于具有兩個以上電子設備(ED)的轉換器來說變得非常具有挑戰性。這對于涉及具有內部控制換相特征的電子設備的轉換器也是如此。此類場景的一個典型示例是由于某些二極管的阻斷狀態而發生的間歇導電模式。
相反,互補模型則易于構建,并能夠捕捉轉換器的所有模式,無需列舉它們,也不假設關于模式順序和切換時間換相時刻的先驗知識。構建功率轉換器互補模型的關鍵思想是將非線性設備(包括二極管和開關)的電壓-電流特性視為網絡動態線性部分的輸入-輸出,可以利用經典電路理論技術進行建模。模型隨后用電子設備的特性進行補充。
構建功率轉換器互補模型的方法是將ED的特性與它們所處電路分開建模,然后將這些表示與電路的動態方程整合。在修改后的節點分析中使用了類似的方法,這是在仿真程序(如PSpice)中采用的建模技術,其中ED的特性通過非線性平滑代數關系詳細表示。相比之下,在這種方法中,ED被假定為理想的,其特性通過分段仿射關系表示,這是一種為建模和仿真便利而選擇的經典方法。
在這種方法中,功率轉換器被表示為線性時不變動態系統(記作Σd)的反饋互連,該系統描述電路拓撲,以及一組分段仿射特性(?,λ),表示電子設備(ED)的電流-電壓特性(見圖1)。在文獻中也稱為Lur’e模型。
可以使用經典電路理論技術,根據功率轉換器的配置推導出Σd的最小狀態空間表示。
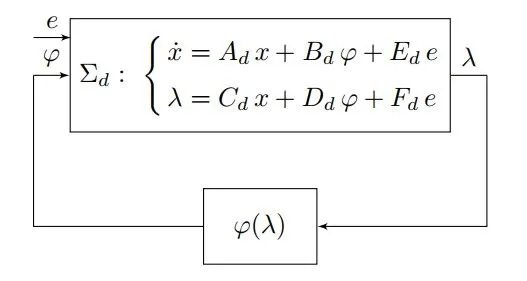 圖1
圖1非遞減的分段仿射ED特性在互補形式中表示,如前一篇文章《開關系統的線性互補模型簡介》中所示。
要構建動態塊Σd的模型,讓我們將每個第i個電子設備(ED)的電流和電壓視為輸入?i或作為電路其余部分的輸出λi,后者代表系統的動態部分。通過提取Ns個ED(由線性元件(電阻器、電感器、電容器)和外部源組成),在非常一般的假設下,所獲得的電路可以通過狀態空間系統描述:
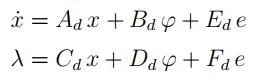
其中,x是狀態向量,e表示外部源,?和λ是具有Ns個分量的向量,使得第i個分量對(?i,λi)表示第i個ED的特性。
二極管的線性互補模型
理想二極管(ID)的電壓-電流特性如圖2所示。可以用互補條件簡單表示:
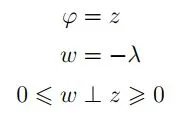
在雙重情況下,當λ是ID電流,?是ID電壓時,通過改變方程2中兩個等式右側的符號可以得到互補模型。電路的拓撲決定了二極管電流應標記為?(從而影響狀態變量的時間導數)還是λ(因此不進入狀態的動態方程,而只滿足代數方程)。
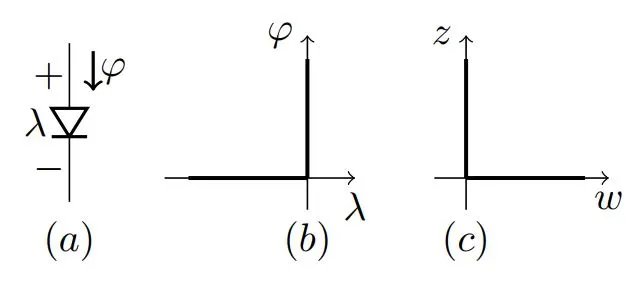 圖2
圖2示例電路
為了展示這種建模技術在實際應用中的應用,我們可以考慮基于半波整流器的電源,如圖3所示。
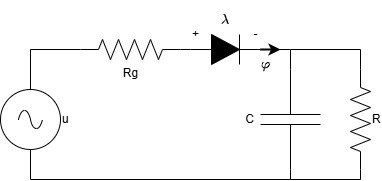 圖3
圖3通過將進入電容器的電流選擇為狀態變量,以及將二極管的互補表示用?作為電流,λ作為電壓,我們可以使用方程2寫出電路的Lur’e表示:
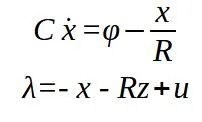 公式3
公式3由此我們最終可以推導出系統的線性互補表示(也稱為線性互補系統):
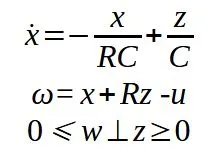 公式4
公式4通過離散化方程4,可以在每個積分步驟中通過解決相應的線性互補問題(LCP)找到解決方案。如所示,一個單一的方程組可以捕捉電路的動態,消除了對二極管每個狀態(導電或阻斷)詳細說明每個等效電路的需要。在經典仿真中(無論是使用可變還是固定步長),求解器必須檢測狀態的切換(例如,通過電流或電壓的零交叉),然后更新下一組方程和狀態變量的初始值。然而,由于現代微處理器的計算能力,這種方法不再是問題。此外,所討論的緊湊表示也對復雜電路的理論分析有價值,因為它使得在一組方程中包含整個系統的動態成為可能。
為了解決這類問題,開發了一種特殊算法,稱為Lemke算法。為了提高找到解決方案的性能,可以在Matlab中使用另一個專用求解器,稱為“路徑”。
仿真結果在以下圖中呈現:?和λ在圖4中描繪,而在圖5中它們相對于最大值進行了歸一化,因此可以注意到它們是非負的,并且從未同時為零,因為它們(在這種特定情況下)對應于互補變量,如圖2所述。
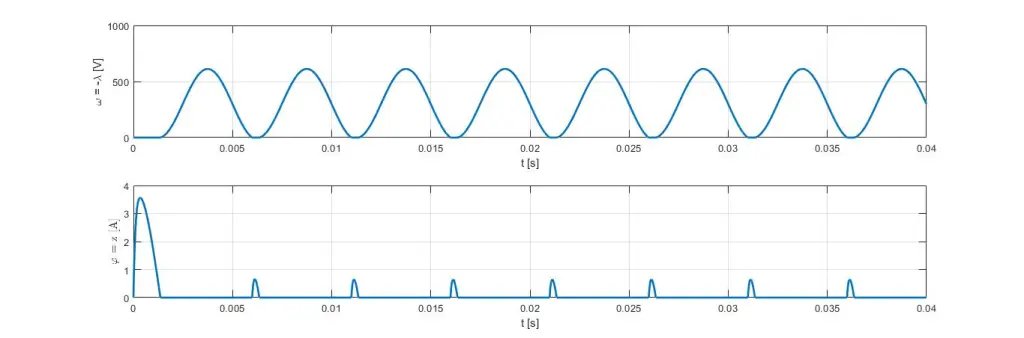 圖4
圖4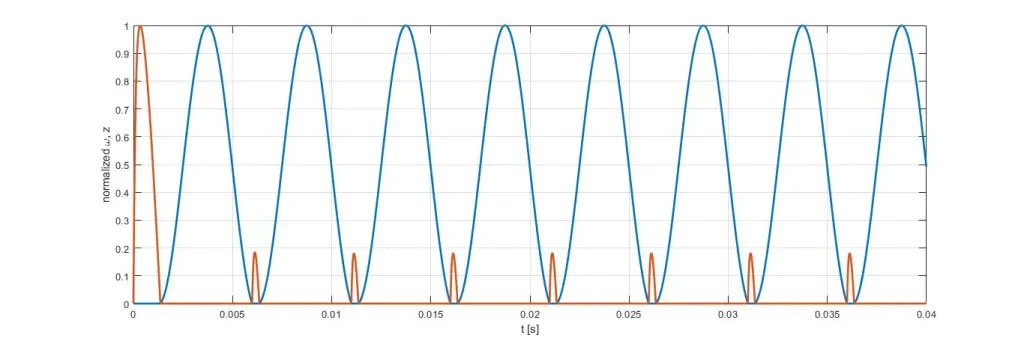 圖5
圖5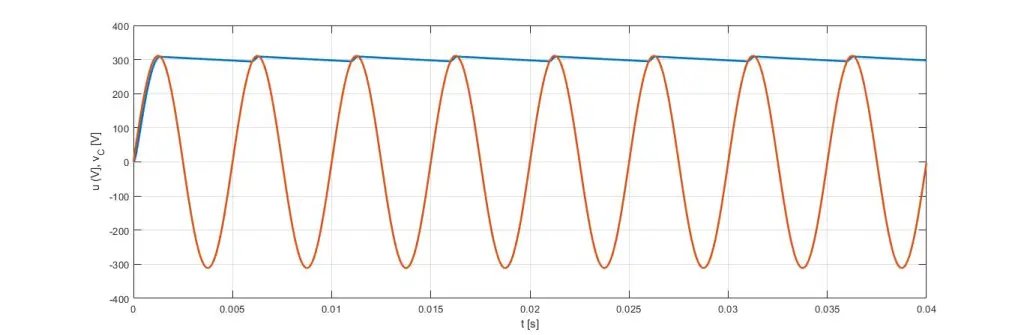 圖6
圖6結論
大多數功率電子電路可以建模為線性動態系統與靜態分段線性特性的反饋互連,這可以使用一組非負互補變量進行描述。集合值函數,例如理想二極管中的電壓-電流關系(電壓為零時,電流可以取任何非負值,或者電流為零時,電壓可以取任何非正值),也可以使用互補變量表示。在這一框架中,可以利用線性互補模型來分析和仿真具有內部切換行為的電路。
-
轉換器
+關注
關注
27文章
8808瀏覽量
149236 -
仿真
+關注
關注
50文章
4177瀏覽量
134687 -
功率電子
+關注
關注
0文章
51瀏覽量
11018
發布評論請先 登錄
相關推薦
功率型LED熱阻測量的新方法
基于線性化技術的二次分配問題求解新方法
提升峰值電流模式控制性能的創新方法




















評論