摘要

量子點半導(dǎo)體光放大器（QD-SOA）具有全光信號處理和光信號再生等突出特點，在光通信系統(tǒng)中得到了廣泛的應(yīng)用。由于這些放大器的納米結(jié)構(gòu)，它們的精確設(shè)計和建模是一個復(fù)雜而具有挑戰(zhàn)性的問題。本文討論了QD-SOA的設(shè)計，提出了一種基于遺傳算法的QD-SOA設(shè)計新方法。由于具有用于設(shè)計的模型是必不可少的，因此在第一步中獲得數(shù)值模型。然后，利用從數(shù)值模型中采樣的訓(xùn)練數(shù)據(jù)建立人工神經(jīng)網(wǎng)絡(luò)模型。實驗表明，該神經(jīng)模型具有較高的精度和較低的計算時間。在下一步中，我們將設(shè)計問題轉(zhuǎn)化為遺傳算法問題。利用神經(jīng)模型，定義了合適的擬合函數(shù)。用戶可以通過設(shè)置設(shè)計參數(shù)的權(quán)重來優(yōu)化生產(chǎn)成本。所提出的系統(tǒng)找到了滿足關(guān)于生產(chǎn)成本的期望增益的最佳解決方案。

1. 引言

目前，量子點半導(dǎo)體光放大器（QD-SOA）被用于光纖通信網(wǎng)絡(luò)中的高速放大和全光信號處理。QD-SOA包含具有量子機械與光相互作用的納米結(jié)構(gòu)層[1]-[2]。

量子點半導(dǎo)體光放大器（SOA）對光信號的放大理論是基于處理電-光相互作用和光脈沖傳播的密度矩陣方程[3]。這讓QD-SOA的設(shè)計非常復(fù)雜。因此，通過智能方法優(yōu)化SOA設(shè)計是非常有益的。遺傳算法（GA）在考慮期望增益的情況下確定模型輸入的最優(yōu)量。對于這種設(shè)計，有一個人工神經(jīng)網(wǎng)絡(luò)（ANN）模型和數(shù)值數(shù)據(jù)是至關(guān)重要的。本文設(shè)計了一種具有期望增益的QD-SOA。QD-SOA的優(yōu)化設(shè)計尚未有文獻(xiàn)報道。

本文內(nèi)容如下：第2節(jié)介紹了QD-SOA的ANN模型；第三節(jié)介紹了遺傳算法的優(yōu)化設(shè)計；第4節(jié)包含結(jié)論。

2.QD-SOA-ANN模型

人工神經(jīng)網(wǎng)絡(luò)基于數(shù)值數(shù)據(jù)的計算來學(xué)習(xí)一般規(guī)則。神經(jīng)網(wǎng)絡(luò)中最小的部分是神經(jīng)元。在圖1中，給出了神經(jīng)元的示意圖。它接收來自其他一些神經(jīng)元的輸入，或者可能來自外部來源。每個輸入x具有相關(guān)聯(lián)的權(quán)重w，該權(quán)重可以被修改以對學(xué)習(xí)進(jìn)行建模。神經(jīng)元計算其輸入的加權(quán)和的一些函數(shù)f：

f是傳遞函數(shù)。一種常見的傳遞函數(shù)是S形函數(shù)，該函數(shù)是神經(jīng)網(wǎng)絡(luò)中經(jīng)常用于在模型中引入非線性和/或確保某些信號保持在指定范圍內(nèi)的數(shù)學(xué)函數(shù)。Sigmoid函數(shù)由以下公式定義：

神經(jīng)網(wǎng)絡(luò)最常見的結(jié)構(gòu)是多層前饋網(wǎng)絡(luò)。在前饋神經(jīng)網(wǎng)絡(luò)中，神經(jīng)元以層的形式組織。一層中的神經(jīng)元從上一層獲得輸入，并將其輸出提供給下一層。在這種網(wǎng)絡(luò)中，不允許連接到相同或先前層中的神經(jīng)元。神經(jīng)元的最后一層稱為輸出層，輸入層和輸出層之間的層稱為隱藏層。輸入層由特殊的輸入神經(jīng)元組成，僅將施加的外部輸入傳輸?shù)狡漭敵觥?/p>

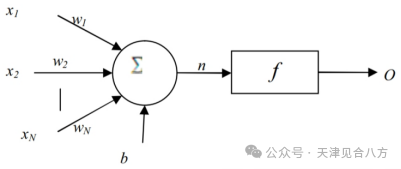
圖1神經(jīng)元示意圖

在一個網(wǎng)絡(luò)中，如果只有一個或多個隱藏層，這種網(wǎng)絡(luò)稱為多層網(wǎng)絡(luò)。反向傳播算法已成為設(shè)計一類特殊的分層前饋網(wǎng)絡(luò)（稱為多層感知器）的主力。

第一步，我們收集了1.3μm波長的InAs/GaAs量子點SOA的數(shù)據(jù)。為此，通過數(shù)值方法對上述QD-SOA進(jìn)行了建模。有關(guān)QD-SOA數(shù)值模型的詳細(xì)信息，請參閱[4]。提出了一種人工神經(jīng)網(wǎng)絡(luò)模型。經(jīng)過幾次嘗試并趨向于更簡單的模型，選擇了一種具有一個隱藏層、四個輸入和一個輸出的前饋神經(jīng)網(wǎng)絡(luò)。該ANN模型的輸入是器件的長度、有源介質(zhì)的有效厚度、施加的電流密度和約束因子，輸出是放大器增益。該模型中使用的算法是反向傳播算法，因為上述算法不需要非常精確的數(shù)據(jù)。所獲得的數(shù)據(jù)分為3部分：訓(xùn)練數(shù)據(jù)集、檢查數(shù)據(jù)集和測試數(shù)據(jù)集。通過訓(xùn)練數(shù)據(jù)集對神經(jīng)網(wǎng)絡(luò)模型進(jìn)行訓(xùn)練。檢查數(shù)據(jù)集用于防止過擬合。測試數(shù)據(jù)集用于評價神經(jīng)網(wǎng)絡(luò)模型。隱藏層和輸出層中的傳遞函數(shù)分別是Sigmoid函數(shù)和Pure line函數(shù)。

我們在隱藏層中使用不同的神經(jīng)元來訓(xùn)練前饋神經(jīng)網(wǎng)絡(luò)模型。性能指數(shù)為均方誤差。由于神經(jīng)網(wǎng)絡(luò)的非最優(yōu)響應(yīng)和收斂到局部極小值，神經(jīng)網(wǎng)絡(luò)被多次訓(xùn)練，訓(xùn)練數(shù)據(jù)沒有得到定期處理。在這種情況下，我們獲得了最好的響應(yīng)。在表1中，顯示了訓(xùn)練ANN的一些結(jié)果。

表1非精細(xì)訓(xùn)練數(shù)據(jù)和不同神經(jīng)元的結(jié)果

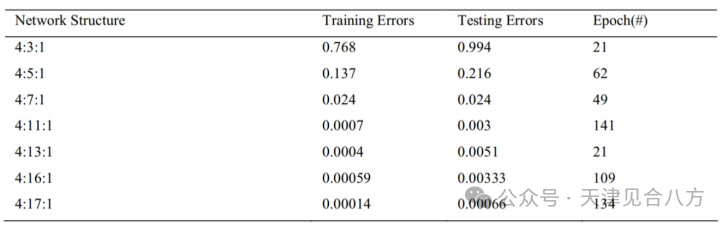
可以看出，對于隱藏層中有17個神經(jīng)元的ANN，獲得了最好的結(jié)果。在該模型中，測試數(shù)據(jù)的均方誤差小于0.0007，表明該模型具有較高的精度。

3.遺傳算法優(yōu)化設(shè)計

遺傳算法是基于達(dá)爾文理論的優(yōu)化算法。它們對設(shè)計參數(shù)的編碼版本進(jìn)行操作，而不是直接對這些參數(shù)本身進(jìn)行操作。基本上，遺傳算法選擇設(shè)計參數(shù)作為“母本”，通過重組親本參數(shù)中的組件來形成“后代”。后代取代系統(tǒng)中的弱參數(shù)，進(jìn)入競爭，在滿足條件時被激活和測試[5]。因此，一種粗略但高速的遺傳算法模擬了進(jìn)化背后的遺傳過程。

在本研究中，目的是設(shè)計具有所需增益的放大器。為了達(dá)到這一目的，需要考慮所需增益來優(yōu)化有效參數(shù)。這意味著有效的參數(shù)被優(yōu)化，而它以最小的成本獲得期望的增益。這種方法使用了遺傳算法。

在建立模型并定義合適的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)用于參數(shù)優(yōu)化后，該方法是通過MATLAB軟件的GA工具箱來獲得所需的增益。首先定義了問題的變量和適應(yīng)度函數(shù)。問題的變量與神經(jīng)網(wǎng)絡(luò)模型的輸入相同。給出了擬合公式：

如圖所示，適合度函數(shù)包含兩個術(shù)語。第一項與算法誤差有關(guān)，其中h為：

和

其中GActual是實際增益，GDesired是從適當(dāng)?shù)腁NN模型獲得的期望增益。第二個術(shù)語與有效參數(shù)有關(guān)，稱為成本函數(shù)。給出了成本函數(shù)：

其中，xi是算法的變量（ANN建模中的4個輸入?yún)?shù)），wi是變量的相關(guān)權(quán)重。wi取決于制造商的條件。這意味著更重要（成本更高）的變量具有更大的權(quán)重。在擬合函數(shù)中，如果實際增益大于期望增益，則省略第一項，僅成本函數(shù)變得重要。擬合函數(shù)的第一項和第二項的值是通過為v選擇合適的值來定義的。

在本研究中，利用MATLAB軟件中的GA工具箱，獲得了17個神經(jīng)元的神經(jīng)網(wǎng)絡(luò)的實際增益，并進(jìn)行了確定優(yōu)化有效參數(shù)的實驗。首先，通過連續(xù)實驗，得到了最佳的擬合函數(shù)和v值。當(dāng)輪盤是選擇函數(shù)，第一種群和交叉分別為40和0.8，并且在最佳條件下，v的值在100到400之間時，實現(xiàn)了最優(yōu)設(shè)計。然后，對于不同的權(quán)重，重復(fù)實驗。這些實驗的結(jié)果如表2所示。

表2遺傳算法設(shè)計QD-SOA的結(jié)果

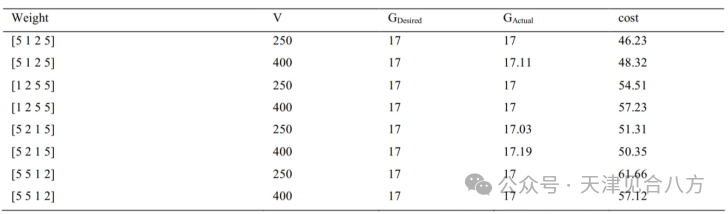
根據(jù)實驗，當(dāng)v值為250，權(quán)重為[5 1 2 5]時，達(dá)到了最佳擬合。一般來說，在考慮期望增益的情況下，遺傳算法在QD-SOA中具有找到有效參數(shù)最優(yōu)值的適當(dāng)潛力。

4.結(jié)論

在這項工作中，提出了一種新的方法來確定考慮期望增益的最優(yōu)模型輸入量。這種方法使用了遺傳算法。根據(jù)遺傳算法的實驗，確定了最優(yōu)設(shè)計的最佳選擇函數(shù)、交叉函數(shù)和第一種群，得到了最佳適應(yīng)度函數(shù)的估計值v。一般來說，所提出的方法在考慮期望增益的材料成本方面給出了合適的結(jié)果。

參考文獻(xiàn)

1. A.J. Zilkie et al, "Carrier Dynamics of Quantum-Dot, Quantum-Dash, and Quantum-Well Semiconductor Optical Amplifiers Operating at 1.55 ?m", IEEE, No. 11 (2007) 43, p-p. 982.991.

2. A. Bilenca et al, "Broad-Band Wavelength Conversion Based on Cross-Gain Modulation and Four-Wave Mixing in InAs–InP QuantumDash Semiconductor Optical Amplifiers Operating at 1550 nm", IEEE, No. 4 (2003) 15, p.p. 563-565.

3. M. Sugawara et al, "Theory of Optical Signal Amplification and Processing by Quantum-Dot Semiconductor Optical Amplifiers", PHYSICAL REVIEW, B, 69(23),235332(39), (2004).

4. F.Hakimiyan et al," Modeling Quantum Dot Semiconductor Optical Amplifier Using Artificial Neural Network", presented in 3rd International Congress on Nanoscience and Nanotecnology(ICNN2010), held by Shiraz University in co-operation with the Iranian Nano Society(INS). 5. R. Haupt et al, Practical Genetic Algorithm, Wiley, New Jersy, 2004.

注：本文由天津見合八方光電科技有限公司挑選并翻譯，旨在推廣和分享相關(guān)SOA半導(dǎo)體光放大器基礎(chǔ)知識，助力SOA技術(shù)的發(fā)展和應(yīng)用。特此告知，本文系經(jīng)過人工翻譯而成，雖本公司盡最大努力保證翻譯準(zhǔn)確性，但不排除存在誤差、遺漏或語義解讀導(dǎo)致的不完全準(zhǔn)確性，建議讀者閱讀原文或?qū)φ臻喿x，也歡迎指出錯誤，共同進(jìn)步。