有限元法(FEM)作為一種分析和設計工具,已廣泛應用于天線、微波和信號完整性等眾多電子工 程領域。FEM求解器與其它矩量法(MoM)和時域有限差分法(FDTD)等數值方法相比擁有多項顯著的優勢。這些優勢包括:能夠處理復雜的非均勻和各向 異性材料、能夠借助四面體單元準確地描繪復雜幾何形狀、能夠使用高階基函數實現準確性、具有多種端口和入射波等激勵方式。利用這些功能優勢,FEM就能夠 以極高的準確性對波導結構進行建模。
但是,對于開放空間問題(例如天線向開放空間輻射的時候),FEM求解器需要通過在人工截斷的邊界 表面上設定輻射邊界條件(RBC),以便將無限域截斷為有限域。兩種廣泛使用的RBC包括一階吸收邊界條件(ABC)和理想匹配層(PML),后者通常情 況下都能夠提供最佳的準確性。兩種方法都保留了FEM系統矩陣的稀疏性,但僅適用于凸起的輻射表面。兩種都屬于近似方法,都存在準確性問題,比如會產生來 自輻射表面的非物理偽反射。這個問題可以通過增大RBC與輻射結構的間距,讓反射降至可忽視的水平,來予以解決。
另一方面,積分方程(IE)法,比如MoM,則非常適合對位于勻質邊界或無限大介質中的結構進行建模。其分析內核采用格林函數,可以在無窮遠處采用Sommerfeld輻射條件。因此,不管是從內存占用,還是從CPU時間占用來說,對多個在空間上分離,互不相連的同質結構,IE求解器都毋庸置疑地成為更好的選擇,因為它不需要對目標之間的空間進行詳細的建模。
早在1990年,Yuan就已經成功實現了FEM求解器和IE求解器的混合算法,這個方法現普遍稱 為混合有限元邊界積分方法(FEBI)。這種方法把邊界積分:Sommerfeld輻射條件的MoM解,用作FEM解的截斷邊界,因此可以在理論上準確地 處理遠場輻射條件。這樣就引出一系列有意思的特性,比如可用作任意形狀的距離輻射體很近的全共形的輻射表面。
本文將介紹ANSYS公司在HFSS中提供的一款全新的FEBI求解器。該求解器得力于近期區域分 解方法的進步。在現有的FEBI方法中,無限未知域被分割為兩個互不重疊的域:一個有界FEM域和一個無界同質外部域。兩個域間的耦合通過其交界面上的合 適的邊界條件加以考慮。
基于域分解的FEBI求解器
FEBI求解器首先將原始的目標域Ω分割為兩個互不重疊的子域Ω1和Ω2,如圖1所示。
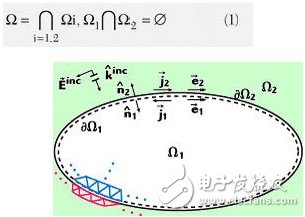
圖1:將目標域分解為FEM域和IE域。
Ω1和Ω2之間的公共界面在FEM域中表達為δΩ1,在IE域中表達為δΩ2.這種區分是必要的, 因為現有的公式允許兩個域間的非共形耦合。也就是說,可以分開處理各個域的網格剖分、基函數和基函數階數、矩陣建立和求解過程。對于一個穩健的FEBI求 解器來說,能夠以模塊化的方式處理每個域的不同基函數階數是非常重要的,因為更高階的IE求解器還在開發的過程中。
根據上述的域分解情況,可以寫出如下最終的系統矩陣:
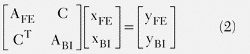
這里,AFE和ABI分別代表FEM域和BI域的系統矩陣。C是兩個域之間的耦合矩陣。由于是通過界面上的電流和磁流來實現耦合的,因此這種耦合非常稀疏。等式2的解可以通過把下式拆分后迭代求得

然后用迭代法求得:
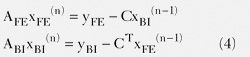
域分解法的優勢可以從4式中清楚地看出。FEM域和BI域被去耦合了,因此并行化就很容易了。上文已經介紹過,BI可以在FEM中用作準確的截斷邊界。由于這種實現方式的模塊化特征,可以輕松地實現先進的FEM求解器和IE求解器的混合求解。
應用
在本節中,將重點介紹使用這種混合方法的兩個例子來突顯FEBI的優勢。如前文所述,一階ABC可 以用于足夠大的有界共形空間,但這個空間不能有凹陷。另一方面,PML可以拉近與模型的間距,但最適合于長方體有界區域。對混合FEBI技術來說,由于可 以精確計算邊界上電流和磁流的耦合,不用考慮這些外形和大小的約束問題。從這種新邊界的測試顯示可以看出,當間距為λ0/10的時候,能夠實現速度和求解 規模的最佳平衡5.這里λ0是開放空間中的波長。另外,FEBI邊界可以做到完全共形,包括凹區域。另外,還可以把模型的各個部分獨立閉合為單獨的域,每 個域都有一個BI邊界。通過使用高度共形和分離空間的區域,可以大幅度縮小有限元求解域的范圍,從而實現高效率的仿真。為證明這一點,下面將介紹兩個例 子,一個使用獨立空間,一個使用高度共形邊界表面。
第一個例子使用的是完全符合教科書的介質透鏡6. 透鏡及其饋源喇叭如圖2所示。透鏡將來自于源天線的電磁場聚焦于正前方。仿真的透鏡采用長方體波導管作為饋源,其εr=2.56,正面直徑為4.4λ0. 然后使用混合FEBI法對系統進行分離域的建模,饋源喇叭及周圍的長方體空間作為一個域,透鏡周圍的圓錐形區域作為另一個域,每個分離空間的截斷面采用 BI邊界。
為便于比較,同時采用了PML對該天線系統進行建模,為求得準確的答案,使用了一個更大的長方體空氣盒 子將整個模型包在內,并距離輻射體足夠的距離以保證結果的準確。與采用PML仿真相比,FEBI模型使用的較小空間可以將內存的占用降低10倍。圖中同時 顯示了兩種仿真計算得出的電場的陰影圖。如其顯示,雖然FEBI仿真使用的分離空間較小,透鏡和喇叭內外和周邊的電磁場都得到了準確的計算,并與PML計 算的結果吻合。喇叭的反射系數(Г)隨與透鏡的距離縮小而增大。在比較加透鏡前后的喇叭端口反射時,兩種仿真都顯示Г有1.8dB的相同增長。圖3是兩種 方法計算得出的該天線系統的前向方向圖。再度體現出FEBI和PML之間的高度吻合。圖2和圖3說明FEBI在使用分離空間來確定天線系統的特性時,具有 相當的準確性。
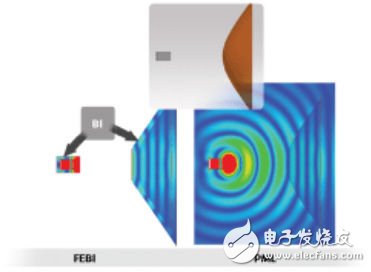
圖2:采用矩形喇叭饋源的介質透鏡。
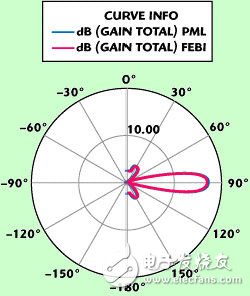
圖3:透鏡的輻射特性。
第二個例子考查的是一組安裝在復雜平臺上的天線陣列(圖4)。它是一個由螺旋天線組成的7元陣列, 安裝在衛星平臺上。衛星兩端之間的長度為18英尺,天線工作頻率3.5GHz.由于這是一個大型模型,所以還是采用域分解法(DDM)來將FEM域分割為 多個較小的域。7這種集成運載平臺的天線系統之前曾采用標準的ABC進行仿真,使用大型閉合長方體空間。該模型閉合的空間的體積大約為 21000λ,DDM將求解范圍分解為34個域。仿真總共需要的存儲為210GB RAM.
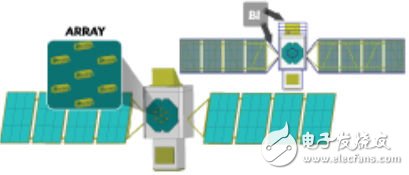
圖4:安裝在衛星上的螺旋天線陣列。
FEBI仿真采用全共形的空間,該共形區域如圖所示。閉合的空間體積下降到1200λ3.由于目標 空間縮小,只需要在12個域上應用DDM,仿真只要21GB的RAM就足夠了。相對于使用標準RBC求解,FEBI仿真所需的存儲大小會大幅度減少。圖5 是兩種仿真在同等幅度和相位激勵下所有天線元的輻射特性,而兩種特性實現了完美的吻合。使用FEBI對位于衛星上的等激勵天線陣列仿真得出的三維極坐標方 向圖如圖6所示。根據這個例子可以了解到,通過將FEBI與高度共形的有界域結合使用,可以在單個桌面計算機上能夠完成大型復雜天線系統的仿真工作。
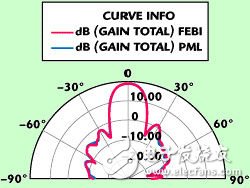
圖5:安裝在衛星上的天線陣列的輻射特性。
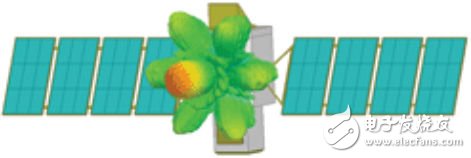
圖6:7元陣列同等激勵下的輻射電磁場三維極化圖。
本文小結
混合FEBI是HFSS的FEM求解器中功能強大的新成員。設計工程師可以利用這種新技術將FEM 仿真的優勢與IE求解器在開放邊界問題上的效率和準確性結合在一起。這個方法對共形區域、凹空間和獨立空間都能取得相當的準確性,可以讓用戶縮小FEM求解域的范圍,從而大幅度縮短求解時間和減少求解所需占用的內存。
-
hfss
+關注
關注
32文章
167瀏覽量
50353
發布評論請先 登錄
相關推薦
新型雷達信號模擬器設計方案
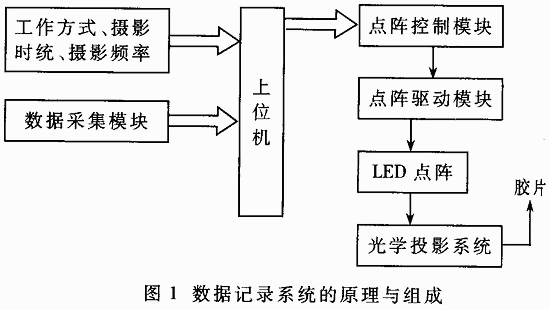
新型的數據記錄系統設計方案
IE和FEBI求解器詳解及對比

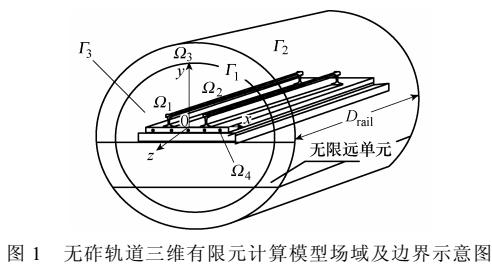
阻抗分解法在無砟軌道阻抗求解中的應用




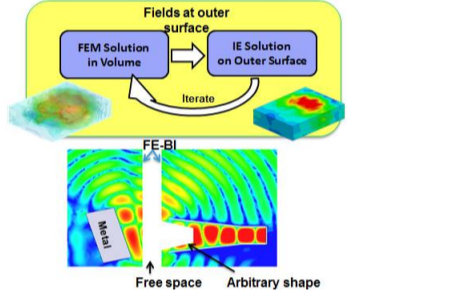
 基于域分解的新型FEBI求解器設計方案
基于域分解的新型FEBI求解器設計方案












評論